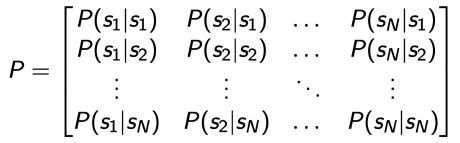强化学习笔记(二)马尔可夫决策过程
马尔可夫决策过程
- 一、马尔可夫过程(MP)
- 二、马尔可夫奖励过程(MRP)
- 三、马尔可夫决策过程(MDP)
- 四、价值函数的求解方法
-
- 1、蒙特卡罗法
- 2、动态规划法
- 3、时序差分学习
- 五、MDP的两个核心问题
-
- 1、预测问题
- 2、控制问题
一、马尔可夫过程(MP)
马尔可夫过程(Markov Process,MP):当前状态的下一个状态只取决于当前状态,与过去状态无关,这样的状态转移过程就是马尔可夫过程,我们也称这样的状态转移是符合马尔可夫的。
马尔可夫链(Markov Chain):符合马尔可夫的状态转移链,如下图所示:

状态转移矩阵(State Transition Matrix):就是一个矩阵,用来记录各种状态转移为其他所有状态的概率。如下图所示:
二、马尔可夫奖励过程(MRP)
马尔可夫奖励过程(Markov Reward Processes,MRP): 在马尔可夫链的基础上加上奖励函数(reward function)。
奖励(reward):即每一步的收益。
折扣率γ(discount factor) :即计算总收益时,将未来收益打折扣。
回报(return) :把奖励进行折扣后所获得的累计收益,一般用字母G表示,如下式所示:
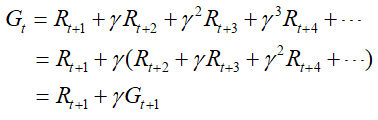
状态价值函数(state value function):在MRP中是指状态s下的回报(return)期望值,如下式所示:

由此,推导出状态价值函数的贝尔曼等式(Bellman Equation),它定义了当前状态跟未来状态之间的关系。如下图所示:

三、马尔可夫决策过程(MDP)
马尔可夫决策过程(Markov Decision Process):在MRP基础上加个动作条件(action)。在MDP中,未来状态不仅依赖当前状态,也依赖当前状态 agent 采取的动作;价值函数值也将由当前状态和动作共同决定。
策略函数(policy function) 或策略(Policy):状态到动作的映射,使状态转移过程具有决策性,这是MDP与MRP的最大不同。
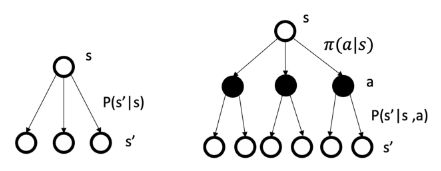
价值函数(value function):回报的期望值,可用来对当前状态或状态-动作对进行估价。马尔可夫决策过程与马尔可夫奖励过程的区别,如下图所示(左侧为MRP,右侧为MDP):
Q 函数(Q-function),即动作价值函数(action-value function),是指策略π下,在状态s时采取动作a的回报值期望,如下式所示:

由此,推导出动作价值函数的贝尔曼等式(Bellman Equation),如下式所示:

Q函数乘以动作概率再进行加和,就可以得到价值函数,即策略π下在状态s时的采取各种动作的总回报期望值,如下式所示:
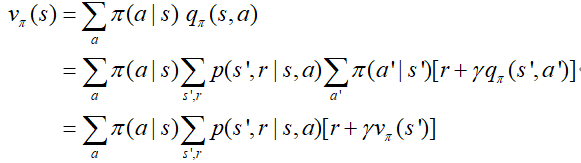
由此,推导出价值函数的贝尔曼等式(Bellman Equation),如下式所示:

在MDP中,我们用价值函数V(s)可以判断当前状态的好坏,用Q函数可以判断在当前状态下做什么动作能够获得最大奖励。
四、价值函数的求解方法
1、蒙特卡罗法
随机生成很多轨迹并计算每条轨迹的回报值,然后取其平均值作为价值函数。
2、动态规划法
使用bootstrapping(拔靴自助)的方法,迭代Bellman Equation,直到最后一步的价值函数值与上一步变化不大(收敛)。
3、时序差分学习
时序差分学习(Temporal-Difference Learning),TD Leanring,结合动态规划和蒙特卡罗的优势,其核心是下面的更新公式:
五、MDP的两个核心问题
1、预测问题
预测(prediction) 问题,也叫 策略评估(Policy evaluation) 问题:给定策略函数(policy function),计算价值函数(value function),其核心思想就是把如下式所示的贝尔曼等式反复迭代,然后就会得到一个收敛的价值函数值。

回溯(backup):类似于bootstrapping之间的迭代关系,即某一个状态的当前价值与未来价值线性相关。
回溯图(backup diagram):表示回溯关系的图,如下图所示,每一个空心圆圈代表一个状态,每一个实心圆圈代表一个状态-动作对。
回溯关系构成了更新或备份操作的基础,这些操作使价值在不同状态间传递,是强化学习方法的核心。
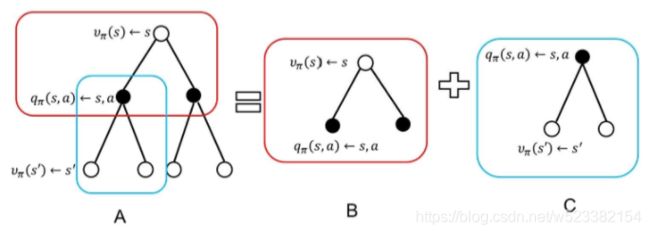
这张回溯图中有两层加和:第一层加和是叶子节点,把未来的价值加和,向上走一层backup到黑色的节点;第二层加和是对 action进行加和,即得到黑色节点的价值后,再往上backup一层得到根节点的价值,也就是当前状态的价值。
2、控制问题
控制(control) 问题:未给定策略,同时求最优策略和最优价值函数,即寻找一个最佳策略(optimal policy) 来得到一个最佳价值函数(optimal value function)。
最佳价值函数的定义如下式所示:
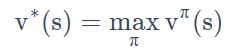
最佳策略的定义如下式所示:
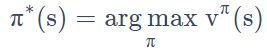
搜索最佳策略有以下两种常用的方法:
(1)Policy iteration:由两个步骤组成:policy evaluation 和 policy improvement。
首先初始化V和π ,然后不断在下面两个步骤之间迭代。
第一个步骤是 policy evaluation:按当前的策略函数(policy function)来估计价值函数(value function)。
第二个步骤是 policy improvement: 对Q函数进行贪心搜索来改进策略函数。
(2)Value iteration:用贝尔曼最优方程去寻找最优的价值函数,然后再提取最佳策略。