分布式深度强化学习的内功修炼之隐式分布

点击蓝字

关注我们

AI TIME欢迎每一位AI爱好者的加入！

为了提高基于策略梯度的强化学习算法的样本效率，我们提出了基于两个深度生成器网络（DGN）和一个更加灵活的半隐式actor（SIA）的隐分布actor-critic 算法（IDAC）。采用分布式强化学习观点，并使用与状态动作相关的隐式分布对其建模，该隐式分布将状态动作对和随机噪声作为其输入的DGN近似。此外，使用SIA来提供半隐式策略分布，该策略分布将策略参数与不受分析密度函数约束的可重新参数化分布混合在一起。这样，该策略的边缘分布是隐式的，提供了对诸如协方差结构和偏度之类的复杂属性建模的潜力，但仍可以进行熵的估计计算。我们将这些功能与off-policy算法框架结合在一起，以解决连续动作空间中的问题，并将IDAC与其他标准算法在OpenAI Gym里进行比较，我们观察到IDAC在大多数任务中都优于这些基准。

岳煜光：本科毕业于复旦大学数学系，现为德州大学奥斯汀分校统计系博士，导师为周名远。主要研究兴趣是贝叶斯统计和强化学习，以及其他与统计相关的强化学习方向如模仿学习。

一、Motivation: 强化学习的局限性在哪里？

强化学习（Reinforcement Learning，RL）是什么？强化学习的目的是：学习从状态（state）到动作（action）的一种映射（map），以获得最大化的收益（reward）。其组成部分，可分为以下5个方面：

●  状态/观测值（state/observation）：当前情况；

●  动作（action）：当前采取的动作以及下一步的动作；

●  奖励（reward）：基于当前的state和action会获得的奖励；

●  策略（policy）：如何做决策；

●  动态环境（environment dynamics）:包括转移矩阵或者环境的核函数。

如何处理强化学习任务？通常分为两类方法：Policy gradient based algorithm 以及Value based algorithm。讲者就第二种方法进行介绍，主要算法步骤如图1所示。其中动作-值函数（Action-Value function）被定义为，在当前策略π的情况下，从初始状态-动作对（State-action pair）开始时期望的累计收益。

具体是使用贝尔曼方程（Bellman equation）计算当前状态-动作对所获得的收益与未来期望的收益之和，从而评价动作-值函数；然后求解在当前状态（state）下，使Action-value function（Q函数）最大化的动作（action），以进一步更新策略，由此反复迭代，直至算法收敛。但由于在深度强化学习（Deep Reinforcement Learning，DRL）中，Action-value function一般是采用深度神经网络来建模，且当action是连续而非离散时，求解arg max函数（神经网络具有非凸性）就显得十分困难。因此，基于DRL框架，在连续动作空间（continuous action space）中，如何克服困难实现策略更新？

图1  value based 算法的介绍

1、第一个motivation

针对上述难点，讲者介绍了Soft Actor-Critic（SAC）的处理方法，即在策略更新时，最小化Q函数玻尔兹曼分布的KL距离。算法的初衷是：由于较难求解动作-值函数的最大值，故使更新后的策略尽可能接近Q函数的manifold，这是因为，假设存在任意flexible的策略，最小化KL散度时，得到的策略应与动作-值函数的manifold一致。

然而实际情况中存在计算的问题，使下述的最小化KL散度的目标函数中包含策略的熵项（entropy term），这要求在建模策略时，应保证可以得到准确的熵估计或者一个近似值，以实现策略更新。一般情况下，使用高斯分布建模策略，继而最小化KL散度，但这会带来很多局限性。

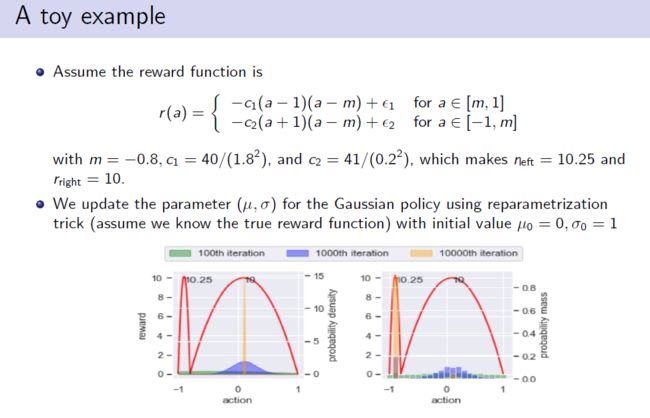
一个简单的toy example解释，假设：1）reward只是从一个action到实数的映射；2）action的诱导分布正比于reward的玻尔兹曼分布。则在强化学习中，最大化加上策略熵后的期望，称为最大化熵强化学习（MERL），其目标函数比正常强化学习的目标函数多了熵的正则项。在训练过程中，通过调整熵，以避免生成策略的过早degenerate，从而获得较好的exploration。根据公式（1）可知，最大化左侧等于最小化右侧的KL散度，该目标函数与变分推断（Variational Inference，VI）中目标函数一致，说明若π_θ(a)服从高斯分布，其只能cover到的p(a)一个模式上，这也是高斯分布带来的缺点，不能coverp(a)的多个模式。

图2 SAC的算法简介

讲者引入一个双峰的奖励函数（reward function）进一步阐述，左峰值是全局最优，右峰值为局部最优。由图可知，随着训练次数增加，左图中采用高斯分布进行策略建模得到的exploration最终收敛至其中一个模式上（局部最优）；而右图是采用flexible的策略（即离散策略），可cover到两个模式上，且最终收敛到全局最优的模式上。

综上，高斯策略在上述目标函数中存在很多局限性，故而讲者提出第一个motivation，构建一种更加flexible的策略来提高策略分布的性能。

图3  实例解释

 

2、第二个motivation

在传统的经典强化学习设置中，动作-值函数一般是一个标量（scalar），但这不是一个很好的模式，基于此，讲者提出的第二个motivation是将分布式强化学习的概念加到连续动作的设置中。

通过在蘑菇数据集上的举例，假设无论蘑菇是有毒或无毒，当前的策略都是“吃”，那么50%的概率会得到positive的反馈，50%是negative的反馈，故而动作-值函数更像是一个随机变量（random variable）而非标量。若动作-值函数强制采用标量表示，即“feeling good”是1，“feeling sick”是-1，如此不能很好地model数据本身的特征。

图4  蘑菇数据集介绍

采用Z^π(z,a)表示distributional version下的动作-值函数（为随机变量），其满足一个条件，即scalar version 下的动作-值函数等于Z^π(z,a)的期望。由此，构建分布式贝尔曼方程，其与贝尔曼方程相似，唯一区别在于公式中的“等于”变为“分布等于”，所以说公式（2）左侧的动作-值函数应等于当前的奖励与未来discounted的动作-值函数之和，这表明等式左右两边应为两个相同的分布而不是值。

这带来的挑战：distributional version下的动作-值函数需要拟合一个分布而不是标量值。早期的工作Categorical DQN（C51），将动作-值函数在值域上分为51个atoms，同时更新他们的probability，并用来表示这个随机变量的分布；另一项工作Quantile regression DQN（QR-DQN）注重处理一些分位数，并基于分位数做回归，然而该两种算法均是基于假设动作空间是离散的情况下进行。

图5  分布式强化学习面临的挑战

二、How：隐式分布的两层内功

基于上述两个motivation，讲者提出了Implicit distribution actor critic（IDAC）的算法，包括以下两个创新点：

1） 将动作-值函数的随机变量的形式引入到continuous setting中，而不单单是discrete setting;

2） 构建一个更加灵活的策略分布，而不是简单的高斯分布。

算法中的“implicit”有两层含义：

1）使用一个深度生成网络（Deep Generator Network，DGN）建模return分布以及Z^π(z,a)，则这个生成器的噪声采用随机噪声生成，并通过一个神经网络来估计Z^π(z,a)。主要过程是：通过采样100个噪声，进行转换，希望转换结果是Z^π(z,a)的100个empirical samples，排序后将其对应于100个不同的分位数，进一步做分位数回归，最小化，从而实现生成器参数的更新；

2）与高斯策略分布和随机噪声分布不同，边缘分布本身是一个较复杂，灵活的分布，具有比如偏度，多模态以及维度间的相关性等特性。构造如此复杂策略的原因，正好解释了上述提及的，在最小化KL散度时，必须能渐进的估计该策略的熵项，才能实现策略更新。

关于如何训练这两个components，详见讲者论文，地址附在文末。

图6  两个“隐式”的指代

三、实验验证

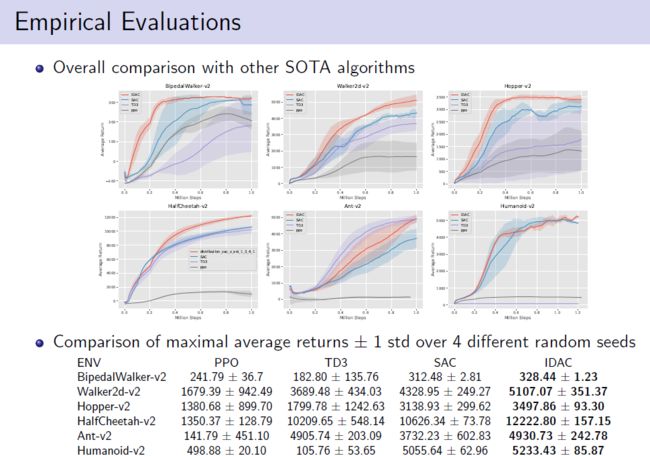
讲者首先进行了empirical evaluation实验对比，红实线为IDAC的性能表现，由对比训练可知，在所有任务上IDAC的表现优于其他算法。

图7  empirical evaluation实验对比

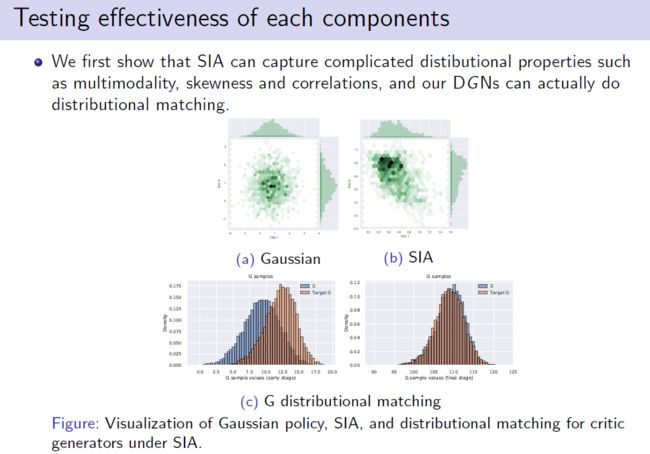
讲者针对IDAC中两个不同的component分别进行实验验证，首先验证了Semi-implicit actor（SIA）的效果，（a）图是采用高斯策略进行建模，得到的边缘分布均为高斯分布；（b）图是指在同样的状态-动作对的情况下，评估SIA的效果，结果表明action dimension之间具有很明显的相关性，明显的偏度，以及较不明显的多模态性，这说明SIA弥补了高斯分布的局限性。然后（c）图中蓝色部分DGN生成的分布与目标分部在训练后期逐渐重合，说明DGN能满足分布式贝尔曼方程。

图8  SIA与DGN的实验验证

最后，通过消融实验，说明了DGN较SIA对学习的帮助更大，且两者结合能实现最大的提高。

图9  消融实验

相关资料

论文下载地址：https://arxiv.org/abs/2007.06159

代码地址：https://github.com/zhougroup/IDAC

 

参考文献：

Marc G Bellemare, Will Dabney, and Rémi Munos. A distributional perspective on reinforcement learning. In Proceedings of the 34th International Conference on Machine Learning-Volume 70, pages 449–458. JMLR. org, 2017.

Will Dabney, Mark Rowland, Marc G Bellemare, and Rémi Munos. Distributional reinforcement learning with quantile regression. In Thirty-Second AAAI Conference on Artificial Intelligence, 2018.

  e           m     t

往期精彩

 AI                i

整理：刘美珍

审稿：岳煜光

排版：岳白雪

AI TIME欢迎AI领域学者投稿，期待大家剖析学科历史发展和前沿技术。针对热门话题，我们将邀请专家一起论道。同时，我们也长期招募优质的撰稿人，顶级的平台需要顶级的你！

请将简历等信息发至[email protected]！

微信联系:AITIME_HY

AI TIME是清华大学计算机系一群关注人工智能发展，并有思想情怀的青年学者们创办的圈子,旨在发扬科学思辨精神，邀请各界人士对人工智能理论、算法、场景、应用的本质问题进行探索，加强思想碰撞，打造一个知识分享的聚集地。

更多资讯请扫码关注

 

（直播回放：https://b23.tv/mhgMUF）

（点击“阅读原文”下载本次报告ppt）