A. Replacing Elements
题意:一个数组,可以用两个不同的元素替换掉另外一个元素,不限次数。问,能否使得数组中所有元素都不大于 d 。
思路:显然,如果所有元素都不大于d,那就执行0次。成立。如果有元素大于d,那就得替换掉,显然选择最小的两个元素进行替换。所以如果最小的两个元素加起来大于d那就没戏了。反之有解。
AC代码:
#include
#define int long long
using namespace std;
const int N = 1e6+7;
const int mod = 1e9+7;
int t,n,m,k;
int a[N],b[N];
vector<int> v1,v2;
signed main(){
cin>>t;
while(t--){
cin>>n>>k;
for(int i =0 ; i < n ; i ++) cin>>a[i];
sort(a,a+n);
int flag = 1;
if(a[n-1] > k){
flag = 0;
}
if(flag) {
cout<<"YES"<<endl;
continue;
}
if(a[0]+a[1] <= k){
cout<<"YES"<<endl;
}else{
cout<<"NO"<<endl;
}
}
return 0;
}
B. String LCM
题意:两个字符串,定义字符串的因子就是,字符串中重复出现的子串。如“abab” 的因子就是“ab”和“abab”,现在要 求两个字符串的lcm。 也就是说,s1,s2,都是lcm的因子。
思路:第一眼没有看到数据范围,浪费了几分钟,数据范围很小。可以直接枚举字符串的因子 p。然后求在s1,s2 中出现的次数c1,c2,取lcm(c1,c2),就是p在要求的字符串的出现次数。
AC代码:
#include
#define int long long
using namespace std;
const int N = 1e6+7;
const int mod = 1e9+7;
int t,n,m,k;
int a[N],b[N];
vector<int> v1,v2;
bool div(string s1,string p){
C. No More Inversions
题意:难以描述。给定一个a数组
a:1,2,3,…,k−1,k,k−1,k−2,…,k−(n−k) (k≤n<2k).
要找一个 p 排列(1-k 的排列)。排列的定义可以自行百度。然后根据a数组和p数组,可以生成一个b数组。 要求是,b数组中的逆序对数量不大于a数组中的逆序对数量,且字典序最大。b的生成规则是:以a数组为p的索引,到p中取数放到b数组中。即b[i] = p[ a[i] ],有点绕。a数组就是当下标用。如 a:[1,2,3,2],那么生成的b数组就是:
b:[ p[1],p[2],p[3],p[2] ] 。
思路:比赛的时候花了很久才看懂题意。然后懵逼了一会,然后开始找规律,然后发现了规律。a数组中的逆序对就是 k ,之后的数。如[1,2,3,4,3,2],就是[4,3,2],这一部分。生成的b数组的后半部分(左右对称的部分)就是[p[2],p[3],p[4],p[3],p[2]],可以发现,如果p数组就是有序的,那么生成的就是 23432,逆序对数量一定是等于a数组的,因为其实就是b数组等于a数组了,一模一样,但是,如果p中这部分值是逆序的,那么生成的就是 43234,逆序对数量也等于a数组!!。那么显然逆序排列是字典序最大的。所以答案就是这个东西了!前面不对称的部分不能改,改了逆序对就比a数组更多。可以尝试证明一下。
AC代码:
#include
#define int long long
using namespace std;
const int N = 1e6+7;
const int mod = 1e9+7;
int t,n,m,k;
int a[N],b[N];
vector<int> v1,v2;
signed main(){
cin>>t;
while(t--){
cin>>n>>k;
int res = n-k;
int tmp = k-res-1;
for(int i = 1 ; i <= tmp ; i ++){
cout<<i<<" ";
}
for(int i = k ; i > tmp ; i --){
cout<<i<<" ";
}
cout<<endl;
}
return 0;
}
D. Program
题意:x,初始为0,两种操作,’+’ 表示 x += 1,’-’ 表示 x -= 1。然后题目给出一系列操作。然后q个询问 l,r。表示删掉区间 [l-r],之内的操作,剩下的操作,可以让x变成多少不同的值。
8 4
-+--+--+
1 8
2 8
2 5
1 1
样例解释:
1.empty program — x was only equal to 0;
2."-" — x had values 0 and −1;
3."---+" — x had values 0, −1, −2, −3, −2 — there are 4 distinct values among them;
4."+--+--+" — the distinct values are 1, 0, −1, −2.
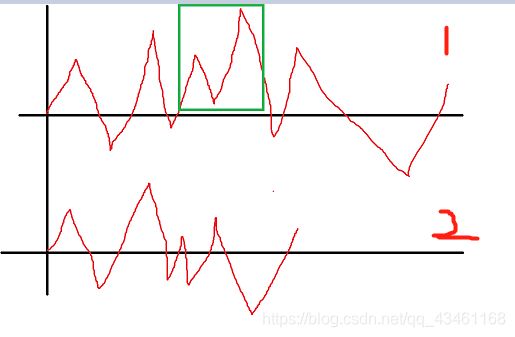
思路:首先考虑在没有删除的情况下,一系列操作过程中,能变成多少不同的值。x初始为0,随着+±-的变化,会来回反复横跳,那么两个关键点就是最大值和最小值,这说明从最大值到最小值之间的数字,都是在操作过程中出现。所以只需要考虑一个区间内的操作产生的最大最小值。但是题目要删掉,中间一段,剩下两段,也就是要把两段合并起来。画个图其实更好理解。红色的是所有的操作,绿色的是要删除的操作,第二个曲线就是合并之后的x值变化曲线。由图可知。后面那部分合并过来之后,起点就是前面那部分的终点!这就是关键点。然后前面那部分的区间的最大最小值和当前值都很好维护。难的是后面那部分怎么维护。后面那部分,从后往前维护,每到一个点,都认为这个点是零点,然后计算最大值最小值。因为是反着来,可以发现操作曲线是一个与 原操作 关于x轴对称的曲线,所以最大值就是最小值,最小值就是最大值。然后最小值就是 当前点到最小值的距离,最大值就是 当前点到最大值的距离。之所以算距离,是因为,永远认为当前点是0点。所以 距离 才是真正的最大最小值。
AC代码:
#include
#define int long long
using namespace std;
const int N = 1e6+7;
const int mod = 1e9+7;
int t,n,m,k;
int a[N],b[N];
int res[N];
vector<int> v1,v2;
struct node{
int maxx,minn,now;
}seg[N],seg2[N];
signed main(){
cin>>t;
while(t--){
cin>>n>>k;
string s;
cin>>s;
int maxx = 0;
int minn = 0;
int now = 0;
for(int i = 0 ; i < n ; i ++){
if(s[i] == '-') now -= 1;
if(s[i] == '+') now += 1;
maxx = max(maxx,now);
minn = min(minn,now);
seg[i].maxx = maxx;
seg[i].minn = minn;
seg[i].now = now;
}
maxx = 0;
minn = 0;
now = 0;
for(int i = n-1 ; i >= 0 ; i --){
if(s[i] == '-') now -= 1;
if(s[i] == '+') now += 1;
maxx = max(maxx,now);
minn = min(minn,now);
seg2[i].maxx = now-minn;
seg2[i].minn = now-maxx;
seg2[i].now = 0;
}
seg[n].maxx = seg2[n].maxx = 0;
seg[n].minn = seg2[n].minn = 0;
for(int i = 0 ; i < k ; i ++){
int x,y;
cin>>x>>y;x--,y--;x--,y++;
int maxx = 0;
int minn = 0;
if(x >= 0){
maxx = max(seg[x].maxx,seg[x].now+seg2[y].maxx);
minn = min(seg[x].minn,seg[x].now+seg2[y].minn);
}else{
maxx = seg2[y].maxx;
minn = seg2[y].minn;
}
res[i] = maxx-minn+1;
}
for(int i = 0 ; i < k ; i ++){
cout<<res[i]<<endl;
}
}
return 0;
}
E. Minimum Path
看完题目,还剩40多分钟,选择挂机,于是挂机了。
