poj1222
貌似又是一个矩阵图形的问题，看起来应该是不太容易，不管了先做做吧！
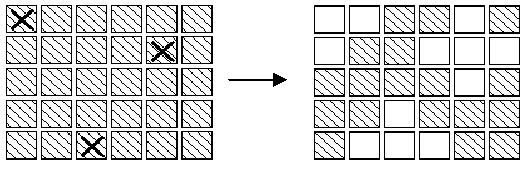（打X的就是准备被按得可以看到右边的有些部分变成了白色）。
题目大意：
题目：灯光延伸出去（延长熄灯）？？
在一个扩展的游戏版本 熄灯，它是一个难题（或者谜）在一个5行每一行有6个按钮（实际是5行每行有5个按钮/////没有扩展的游戏？？），在每一个按钮上都有一个灯，当一个按钮被压下去的时候，这个灯和它四周的的（上下左右）的灯的状态将会被逆转（有木有很像昨晚做的那个反转游戏！！！不过5行6列就是2^30，不能用那个方法做了貌似），如果是开着的那么灯将被关闭，如果是关闭的那么灯将会被打开，在角落里的按钮只可以改变三个按钮的状态（邻近的按钮），在边上的按钮可以改变4个按钮的状态，其他的可以改变5个，例如下面的图像
（打X的就是准备被按得可以看到右边的有些部分变成了白色）。
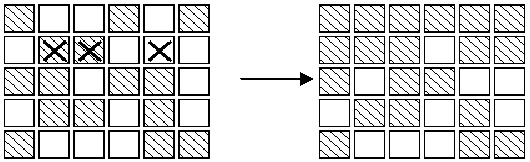
这个游戏的目标是，从任何初始灯的状态开始，通过按压按钮让所有的灯都显示关闭，当按钮被按压后，邻近的按钮可以撤销他带来的影响（应该是恢复自身和刚才那个按钮的状态，应该是不会对别的按钮产生影响），例如，在下面图像的显示
注意：
1，不管你以什么顺序按下按钮。
2，如果第二次按下按钮，那么它会完全取消第一次按下的影像，所以没有按钮需要按两次。
3，在第二个图示中，第一行所有的等都会被关闭，在第二行按下相应的按钮，在每一行重复这个过程（如果上面是白色的，那么是不是只要在下一行对应的位置按一下就好了呢？？）上面灯的状态就会转化到下一行吧
输入一个5*6的矩阵由0和1表示的，0代表灯关闭1代表开着，那么输出一个同样的矩阵也是由0和1表示0代表不按，1代表这个按钮被按过
//////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
题目模拟//
0 1 1 0 1 0 0 0 0 0 0 0
1 0 0 1 1 1 0 1 0 0 0 0
0 0 1 0 0 1 --> 0 0 0 0 0 0
1 0 0 1 0 1 0 0 0 0 0 0
0 1 1 1 0 0 0 0 0 0 0 0
0 0 1 0 1 0 0 0 0 0 0 0
0 1 1 1 1 1 0 1 1 0 0 0
0 1 1 0 0 1 --> 0 0 0 0 0 0
1 0 0 1 0 1 0 0 0 0 0 0
0 1 1 1 0 0 0 0 0 0 0 0
0 0 0 0 1 1 0 1 1 0 1 0
0 1 0 0 0 1 --> 0 0 0 0 0 0
1 0 0 1 0 1 0 0 0 0 0 0
0 1 1 1 0 0 0 0 0 0 0 0
0 0 0 1 0 0 0 1 1 0 1 0
0 1 0 0 1 1 --> 0 0 0 1 0 0
1 0 0 1 0 1 0 0 0 0 0 0
0 1 1 1 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 1 1 0 1 0
0 1 1 1 0 1 --> 0 0 0 1 0 0
1 0 0 0 0 1 0 1 0 0 0 0
0 1 1 1 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 1 1 0 1 0
0 0 1 1 0 1 --> 0 0 0 1 0 0
0 1 1 0 0 1 0 1 1 0 0 0
0 0 1 1 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 1 1 0 1 0
0 0 0 1 0 1 --> 0 0 0 1 0 0
0 0 0 1 0 1 0 1 1 1 0 0
0 0 0 1 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 1 1 0 1 0
0 0 0 0 0 1 --> 0 0 0 1 0 0
0 0 1 0 1 1 0 1 1 1 0 1
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 1 1 0 1 0
0 0 0 0 0 0 --> 0 0 0 1 0 0
0 0 1 0 0 0 0 1 1 1 0 1
0 0 0 0 0 1 0 0 0 0 0 0从上面的模拟过程中可以看出来这样的方式还是有点问题存在，那么就是把所有的灯都压到了最后一行，那么最后一行应该怎么解决呢？？？？？似乎有一些行不通/////////////////////////////////////////////////////////////////////////////////////////实在是没有什么思路所以看了一下题解，题解貌似都是什么高斯消元，听起来很高大上，不过不明白就是了，看了另外一个题解报告说是只要枚举第一行就行，只要第一行固定了那么下面的也就固定了，听起来是很有道理的，只要第一行是固定的那么下面的就按照上面的那种方式来就行了，直到找到一组解（http://www.hankcs.com/program/algorithm/poj-1222-extended-lights-out.html）。先按照这种理解方式做一下吧。因为是枚举第一行，所以产生的状态也就是2^6,应该还是一个很小的数字。测试数据确实没有问题，不过提交后无情的给了一个WA！！！为啥呢？？？？好吧，我也不知到为什么，不过可以测试一下数据
找到BUG搜索应该从0开始的///////////////////////////////for(i=1; i<64; i++) 跟上一次做题的时候错的差不多，我晕，认栽了，仔细确实不能只嘴上说说的
#include<stdio.h>
#include<
string.h>
#include<iostream>
using
namespace std;
#define maxn 10
//
2^6 = 64
int dir[
5][
2] = {{
0,
0},{
0,
1},{
1,
0},{-
1,
0},{
0,-
1}};
int c[
10][
10];
void changeXY(
int b[][
10],
int x,
int y);
//
把xy坐标和四周的坐标改变
int OK(
int x,
int y);
//
判断xy坐标是否合法
int Find(
int b[][
10]);
//
第一行固定后，往下面查找，看看最后一行是否会变为全0
int main()
{
int T, t=
1;
scanf(
"
%d
", &T);
while(T--)
{
int i, j, k,a[
10][
10], b[
10][
10];
for(i=
1; i<=
5; i++)
for(j=
1; j<=
6; j++)
scanf(
"
%d
", &a[i][j]);
for(i=
0; i<
64; i++)
{
for(j=
1; j<=
5; j++)
for(k=
1; k<=
6; k++)
b[j][k] = a[j][k], c[j][k] =
0;
k = i;
for(j=
6; j>
0; j--)
{
if(k %
2)
{
changeXY(b,
1, j);
c[
1][j] =
1;
}
k /=
2;
}
if(Find(b) ==
1)
break;
}
printf(
"
PUZZLE #%d\n
", t++);
for(i=
1; i<=
5; i++)
for(j=
1; j<=
6; j++)
printf(
"
%d%c
", c[i][j], j ==
6 ?
'
\n
' :
'
');
}
return
0;
}
void changeXY(
int b[][
10],
int x,
int y)
//
把xy坐标和四周的坐标改变
{
int i, nx, ny;
for(i=
0; i<
5; i++)
{
nx = x + dir[i][
0];
ny = y + dir[i][
1];
if(OK(nx, ny))b[nx][ny] =
1 - b[nx][ny];
}
}
int OK(
int x,
int y)
//
判断xy坐标是否合法
{
if(x >
0 && x <
6 && y >
0 && y <
7)
return
1;
return
0;
}
int Find(
int b[][
10])
//
第一行固定后，往下面查找，看看最后一行是否会变为全0
{
int i, j;
for(i=
1; i<=
4; i++)
for(j=
1; j<=
6; j++)
{
if(b[i][j])
{
changeXY(b, i+
1, j);
c[i+
1][j] =
1;
}
}
for(i=
1; i<=
6; i++)
if(b[
5][i])
return
0;
return
1;
}