机器学习实战python实例（2）SVM优化

简易版的SVM中，SMO算法中α的选择采取遍历且随机的方式，见http://blog.csdn.net/xiaonannanxn/article/details/52372085
优化版中，我们采取启发式方式选择，即αj选择max|Ei-Ej|，这样就可以让每次更新的步长更大，减少我们的迭代次数，更新上次的SVM.py

# coding:utf-8
from numpy import *
import matplotlib.pyplot as plt

def loadDataSet(filename):
    dataMat = []
    labelMat = []
    fr = open(filename)
    for line in fr.readlines():
        lineArr = line.strip().split('\t')
        dataMat.append([float(lineArr[0]), float(lineArr[1])])
        labelMat.append(float(lineArr[2]))
    return dataMat, labelMat


def selectJrand(i, m):
    j = i
    while j == i:
        j = int(random.uniform(0, m))
    return j


def clipAlpha(aj, H, L):
    if aj > H:
        aj = H
    if aj < L:
        aj = L
    return aj


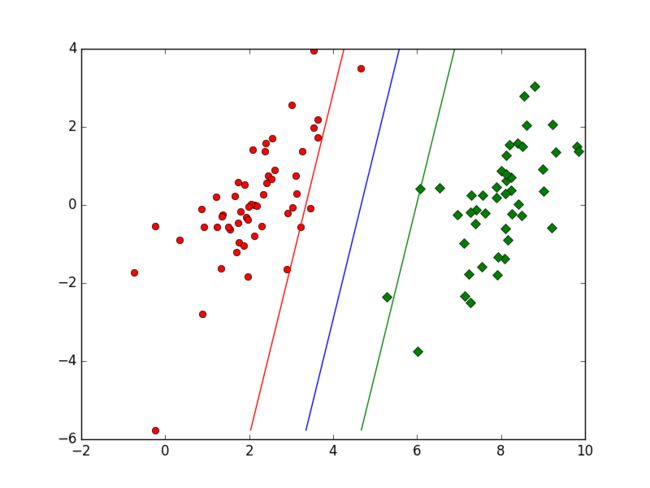
def show(dataArr, labelArr, alphas, b):
    for i in xrange(len(labelArr)):
        if labelArr[i] == -1:
            plt.plot(dataArr[i][0], dataArr[i][1], 'or')
        elif labelArr[i] == 1:
            plt.plot(dataArr[i][0], dataArr[i][1], 'Dg')
    # print alphas.shape, mat(labelArr).shape, multiply(alphas, mat(labelArr)).shape
    c = sum(multiply(multiply(alphas.T, mat(labelArr)), mat(dataArr).T), axis=1)
    minY = min(m[1] for m in dataArr)
    maxY = max(m[1] for m in dataArr)
    plt.plot([sum((- b - c[1] * minY) / c[0]), sum((- b - c[1] * maxY) / c[0])], [minY, maxY])
    plt.plot([sum((- b + 1 - c[1] * minY) / c[0]), sum((- b + 1 - c[1] * maxY) / c[0])], [minY, maxY])
    plt.plot([sum((- b - 1 - c[1] * minY) / c[0]), sum((- b - 1 - c[1] * maxY) / c[0])], [minY, maxY])
    plt.show()


class optStruct:
    def __init__(self, dataMatIn, classLabels, C, toler):
        self.X = dataMatIn
        self.labelMat = classLabels
        self.C = C
        self.tol = toler
        self.m = shape(dataMatIn)[0]
        self.alphas = mat(zeros((self.m, 1)))
        self.b = 0
        self.eCache = mat(zeros((self.m, 2)))


def calcEk(oS, k):
    fXk = float(multiply(oS.alphas, oS.labelMat).T * (oS.X * oS.X[k, :].T)) + oS.b
    Ek = fXk - float(oS.labelMat[k])
    return Ek


def selectJ(i, oS, Ei):
    maxK = -1
    maxDeltaE = 0
    Ej = 0
    oS.eCache[i] = [1, Ei]
    validEcacheList = nonzero(oS.eCache[:, 0].A)[0]
    if len(validEcacheList) > 1:
        for k in validEcacheList:
            if k == i:
                continue
            Ek = calcEk(oS, k)
            deltaE = abs(Ei - Ek)
            if deltaE > maxDeltaE:
                maxK = k
                maxDeltaE = deltaE
                Ej = Ek
        return maxK, Ej
    else:
        j = selectJrand(i, oS.m)
        Ej = calcEk(oS, j)
    return j, Ej


def updateEk(oS, k):
    Ek = calcEk(oS, k)
    oS.eCache[k] = [1, Ek]


def innerL(i, oS):
    Ei = calcEk(oS, i)
    if ((oS.labelMat[i] * Ei < -oS.tol) and (oS.alphas[i] < oS.C))\
            or ((oS.labelMat[i] * Ei > oS.tol) and (oS.alphas[i] > 0)):
        j, Ej = selectJ(i, oS, Ei)
        alphaIold = oS.alphas[i].copy()
        alphaJold = oS.alphas[j].copy()
        if oS.labelMat[i] != oS.labelMat[j]:
            L = max(0, oS.alphas[j] - oS.alphas[i])
            H = min(oS.C, oS.C + oS.alphas[j] - oS.alphas[i])
        else:
            L = max(0, oS.alphas[j] + oS.alphas[i] - oS.C)
            H = min(oS.C, oS.alphas[j] + oS.alphas[i])
        if L == H:
            print "L == H"
            return 0
        eta = 2.0 * oS.X[i, :] * oS.X[j, :].T - oS.X[i, :] * oS.X[i, :].T - oS.X[j, :] * oS.X[j, :].T
        if eta >= 0:
            print "eta >= 0"
            return 0
        oS.alphas[j] -= oS.labelMat[j] * (Ei - Ej) / eta
        oS.alphas[j] = clipAlpha(oS.alphas[j], H, L)
        updateEk(oS, j)
        if abs(oS.alphas[j] - alphaJold) < 0.00001:
            print "j not moving enough"
            return 0
        oS.alphas[i] += oS.labelMat[j] * oS.labelMat[i] * (alphaJold - oS.alphas[j])
        updateEk(oS, i)
        b1 = oS.b - Ei - oS.labelMat[i] * (oS.alphas[i] - alphaIold) * oS.X[i, :] * oS.X[i, :].T \
                - oS.labelMat[j] * (oS.alphas[j] - alphaJold) * oS.X[i, :] * oS.X[j, :].T
        b2 = oS.b - Ej - oS.labelMat[i] * (oS.alphas[i] - alphaIold) * oS.X[i, :] * oS.X[j, :].T \
                - oS.labelMat[j] * (oS.alphas[j] - alphaJold) * oS.X[j, :] * oS.X[j, :].T
        if 0 < oS.alphas[i] < oS.C:
            oS.b = b1
        elif 0 < oS.alphas[j] < oS.C:
            oS.b = b2
        else:
            oS.b = (b1 + b2) / 2.0
        return 1
    else:
        return 0


def smoP(dataMatIn, classLabels, C, toler, maxIter, kTup=('lin', 0)):
    oS = optStruct(mat(dataMatIn), mat(classLabels).transpose(), C, toler)
    Iter = 0
    entireSet = True
    alphaPairsChanged = 0
    while Iter < maxIter and (alphaPairsChanged > 0 or entireSet):
        alphaPairsChanged = 0
        if entireSet:
            for i in xrange(oS.m):
                alphaPairsChanged += innerL(i, oS)
            print "fullSet, iter: %d i:%d, pairs changed %d" % (Iter, i, alphaPairsChanged)
            Iter += 1
        else:
            nonBoundIs = nonzero((oS.alphas.A > 0) * (oS.alphas.A < C))[0]
            for i in nonBoundIs:
                alphaPairsChanged += innerL(i, oS)
                print "non-bound, iter: %d i:%d, pairs changed %d" % (Iter, i, alphaPairsChanged)
            Iter += 1
        if entireSet:
            entireSet = False
        elif alphaPairsChanged == 0:
            entireSet = True
        print "iteration number: %d" % Iter
    return oS.b, oS.alphas

在main.py中测试

import SVM

dataArr, labelArr = SVM.loadDataSet('testSet.txt')
b, alphas = SVM.smoP(dataArr, labelArr, 0.6, 0.001, 40)
SVM.show(dataArr, labelArr, alphas, b)

测试结果