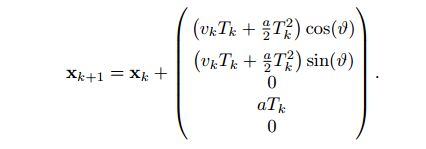利用卡尔曼滤波进行状态估计

本文主要介绍如何利用卡尔曼滤波进行状态估计，因为需要用到一些车辆的运动模型，所以首先简单介绍几种常见的模型

车辆运动模型

匀速模型（Constant Velocity, CV）

四个状态变量依次为横坐标，纵坐标，与x轴夹角（逆时针为正），线速度
匀速和匀加速模型的状态转移方程都很好理解，可以直接得到

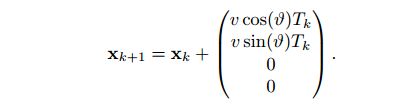
匀加速模型（Constant Acceleration, CA）

状态变量多了一个加速度

恒定速度和转速模型（Constant Turn Rate and Velocity, CTRV）

恒定速度和转速可以看做一段圆弧运动


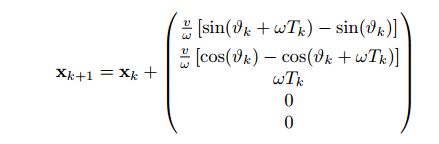
该模型利用简单的几何关系也不难得到，后面两个模型稍微复杂一些。另外，CTRV实际上是CV的一般形式，当$\omega =0$时（这里需要用到洛必达法则），就是CV的形式。

恒定加速度和转速模型（Constant Turn Rate and Acceleration, CTRA）

同CTRV相比，转速不变，说明在相同时间内转过的角度是一样的，径向由匀速变成匀加速，那么对应的，位移会变长（可以参见CCA部分橘色轨迹）


其中

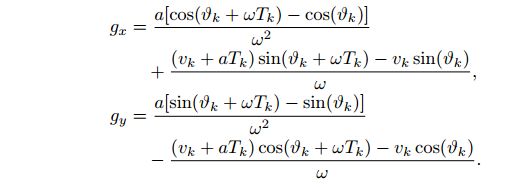
这个模型怎么得到呢？首先$\theta$和$v$的增量我们很好理解，而前两项利用CTRV的结果结合微元法，假设从t时刻开始，经历一个很小的时间dt内我们可以将CTRA模型近似为CTRV模型（回忆一下一起物理中利用微元法推导匀加速运动的过程），那么，dt时间内x，y的增量可以表示为
$${\Delta }_x=\frac{v+at}{\omega }[\sin ({\theta }_k+\omega t+wdt)-\sin ({\theta }_k+\omega t)]$$
$${\Delta }_y=\frac{v+at}{\omega }[\cos ({\theta }_k+\omega t)-\cos ({\theta }_k+\omega t+wdt)]$$
化简，当dt为小量时，${\Delta }_x$可以近似为
$${\Delta }_x=\frac{v+at}{\omega }\cos ({\theta }_k+\omega t)wdt$$
对该式从0到t积分，利用分部积分即可得到结果。

恒定曲率半径和加速度模型（Constant Curvature and Acceleration, CCA）

最后一种模型是将CTRA中的转速一定改为曲率半径一定，由$r=v/\omega$可知，当曲率半径一定，又要做匀加速运动，那么角速度必然是时变的，因此同样时间内转过的角度必然会增大。CTRV（黑），CTRA（橘），CCA（红）的关系如下图所示

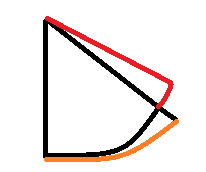
设曲率半径$c=1/r$，则状态变量如下

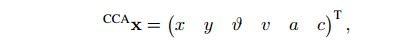
此时，弧长为

则对应的旋转角$b_{k}c$，知道角度了求解转移关系的方法和CTRV一样，最后结果为
$$x_{k+1}=x_k+\left[\begin{array}{c}1/c(\sin (\theta +b_{k}c)-\sin \theta )\\ 1/c(\cos \theta -\cos (\theta +b_{k}c))\\ b_{k}c\\ a{T}_k\\ 0\\ 0\end{array}\right]$$
最后总结一下上述几种模型的关系如下

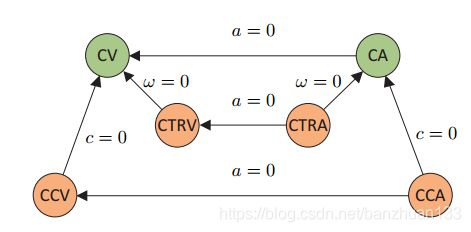
卡尔曼滤波

卡尔曼滤波是最常见的状态估计算法，具体公式的推导相关博客很多，比如卡尔曼滤波 – 从推导到应用(一)，这里就不赘述了，直接贴最终结果
预测过程
$$x_k^{\prime }=A{\hat{x}}_{k-1}+B{u}_k$$ $$P_k^{\prime }=A{P}_{k-1}{A}^T+Q$$
更新过程
$$G_k=P_k^{\prime }{C}^T(C{P}_k^{\prime }{C}^T+R{)}^{-1}$$ $${\hat{x}}_k=x_k^{\prime }+G_k(z_k-C{x}_k^{\prime })$$ $$P_k=(I-G_{k}C)P_k^{\prime }$$
这里的${\hat{x}}_k$就是我们所要的最优估计，$P_k$表示最优估计值的误差，C为观测矩阵，可以理解为 $$z_k=C{x}_k+W$$这里Q，R，W都是误差矩阵。重点是要理解卡尔曼滤波的基本逻辑，我们把更新过程的最优状态估计做个变形
$${\hat{x}}_k=x_k^{\prime }+G_k(z_k-C{x}_k^{\prime })=(I-G_{k}C)x_k^{\prime }+G_k{z}_k$$
$x_k^{\prime }$是基于k-1时刻的最优估计和模型（先验分布）得到的预测值，$z_k$是k时刻的观测值，也就是说，我们的最优估计实际上是对测量值和预测值的一个加权平均，而$P_k$就是迭代过程中的最优加权系数（实际上是根据方差确定比例）。

扩展卡尔曼滤波（EKF）

卡尔曼滤波的优点有很多，但同样也有一个问题，只适用于线性模型，对上面几种模型来说，出现非线性项（比如cos, sin）时，就无法利用上面的结论了。处理非线性问题最常见的一种思路就是线性化，而对线性化我们有一种强大的工具-泰勒展开。多元函数的泰勒展开如下：

其中，$Df(u)$是在该处的雅克比矩阵。一般我们就考虑一阶雅克比矩阵进行线性化近似。举个例子，我们都知道毫米波雷达的预测映射到策略空间是非线性的，表达式如下

其对应的雅克比矩阵为

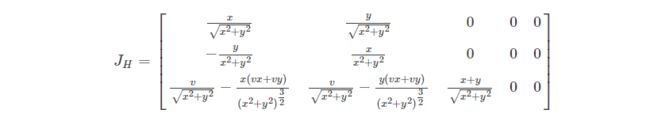
状态估计

讲了这么多，怎么利用卡尔曼滤波来进行状态估计呢？毫米波这个稍微复杂了些，用一个简单的CV模型来示例。假设现在我们有一辆车做匀速直线行驶，则过程模型为
$$x_{k+1}=\left[\begin{array}{c}x+v\cos (\theta )\Delta t\\ y+v\sin (\theta )\Delta t\\ \theta \\ v\end{array}\right]$$
对应的雅克比矩阵为
$$\left[\begin{array}{cccc}1& 0& -v\sin (\theta )\Delta t& \cos (\theta )\Delta t\\ 0& 1& v\cos (\theta )\Delta t& \sin (\theta )\Delta t\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right]$$
由于是匀速过程，那么这里$u_k=0$，对于过程噪声，实际上就是车子突然的加速或减速运动，因此可以认为协方差矩阵Q满足$Q=G{G}^T$，其中
$$G=[0.5a_x\Delta t^2,0.5a_y\Delta t^2,0,a\Delta t{]}^T$$
对于观测矩阵，一般汽车就只能读到实时速度，因此$C=[0,0,0,1]$，对应的协方差矩阵为$R={\delta }_v^2$，R为观测噪声
我们要做一件什么事呢？在测量值只有速度，存在过程噪声和测量噪声的情况下，利用卡尔曼滤波去得到一个最优的状态估计

#! /usr/bin/env python
# -*- coding: UTF-8 -*-
import numpy as np
import matplotlib.pyplot as plt
import math

## KF参数
x = np.matrix([[0.0, 0.0, 0.0, 0.0]]).T #状态变量[x, y, theta, v]
P = np.diag([1.0, 1.0, 1.0, 1.0]) #误差矩阵
dt = 0.1 # 时间间隔
theta = math.pi/6
v = 10 # 速度
F = np.matrix([[1.0, 0.0, -v * math.sin(theta) * dt, math.cos(theta) * dt],
              [0.0, 1.0, v * math.cos(theta) * dt,  math.sin(theta) * dt],
              [0.0, 0.0, 1.0, 0.0],
              [0.0, 0.0, 0.0, 1.0]]) #状态转移矩阵

H = np.matrix([[0.0, 0.0, 0.0, 1.0]]) #观测矩阵
R = 0.25 # 观测方差
deltav = 0.5
G = np.matrix([[0.5*dt**2],
               [0.5*dt**2],
               [0],
               [dt]])
Q = G*G.T*deltav**2 #过程协方差矩阵
I = np.eye(4)
m = 200 # 测量数据数


## 数据存储变量
xt = []
yt = []
thetat= []
vt= [] #v估计值
Zv = [] #v观测值


## 保存过程变量
def saveStates(x, Z):
    xt.append(float(x[0]))
    yt.append(float(x[1]))
    thetat.append(float(x[2]))
    vt.append(float(x[3]))
    Zv.append(float(Z[0]))

## 卡尔曼滤波
def KFfilter():
    global x, P, S, K, Z, y
    for n in range(m):
        ## 预测过程
        x = F*x
        P = F*P*F.T + Q
        S = H*P*H.T + R
        K = (P*H.T) * np.linalg.pinv(S)

        # 更新过程
        Z = v + np.random.randn(1)  # 测量值
        y = Z - (H*x)
        x = x + (K*y)
        P = (I - (K*H))*P
        saveStates(x, Z)

def plot_x():
    fig = plt.figure(figsize=(16,9))
    plt.plot(range(m),vt, label='$estimateV$')
    plt.plot(range(m),Zv, label='$measurementV$')
    plt.axhline(v, color = 'red', label='$trueV$')
    plt.xlabel('Filter Step')
    plt.title('KF Filter')
    plt.legend(loc='best')
    plt.ylim([5, 15])
    plt.ylabel('Velocity')
    plt.show()

if __name__ =='__main__':
    KFfilter()
    plot_x()

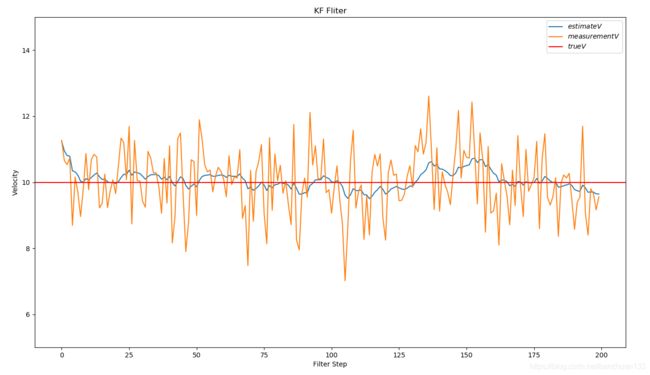
最终结果如下

上图橘黄色的测量值，蓝色是估计值，因为开始我们给的初始值是0，所以一开始误差比测量值大（调整P的初始值可以减小该误差），但是很快就根据测量值做了纠正，最终得到比测量值更接近真实值（红色）的结果。
上面我们是先手动计算雅克比矩阵，实际上python中有专门计算梯度和雅克比矩阵的库numdifftools，比如实现对CV模型的雅克比求解如下

#! /usr/bin/env python
# -*- coding: UTF-8 -*-
import numpy as np
import math
import numdifftools as nd

dt = 0.5
def f(x):
    return np.array([x[0]+math.cos(x[2])*x[3]*dt,
                         x[1]+math.sin(x[2])*x[3]*dt,
                         x[2], x[3]])
Jfun = nd.Jacobian(f)
print(Jfun([1,2,math.pi,3]))

得到的结果如下，可以代入上面手动求解的结果对照

[[ 1.   0.   0.  -0.5]
 [ 0.   1.  -1.5  0. ]
 [ 0.   0.   1.   0. ]
 [ 0.   0.   0.   1. ]]

无损卡尔曼滤波（UKF）

利用线性化方法来解决非线性问题是一种思路，这种方法不足的地方主要有两点，一是雅克比矩阵计算量比较大，二是高度非线性的时候误差可能比较大。除了EKF之外呢，还有一种常见的卡尔曼滤波改进方法——无损卡尔曼滤波（UKF）。
我们举个例子来说明EKF和UKF的逻辑不同点。我们假设车辆的运动符合高斯分布，比如当前在10m的位置，速度为1m/s，那么车下一时刻的位置理论上应该服从均值为11的高斯分布，想象如果车的运动是完全随机的，那我们的估计就没有意义了。那么从这种逻辑出发，对于复杂模型，如果我们知道了k-1时刻的高斯分布，对k时刻，一种方法是找一个线性变换对原来的高斯分布进行映射，得到一个新的高斯分布，这就是EKF。另一种逻辑是，既然下一时刻也服从高斯分布，去线性变换是否不太准确，可以不去线性化而是去找一个同下一时刻的真实分布相接近的高斯分布吗，这就是UKF。
考虑如下非线性系统

我们怎么去估计下一时刻的分布呢？当然，你可能会说，既然已经有系统模型了，我采样它一万八千个点，顺次计算下一时刻的位置，再拟合一个高斯分布，这样不就行了。逻辑上是讲得通的，但是既然我们说EKF计算量大，那么采一万个点肯定不合适，有没有一种简单愉快的采样方式呢？
答案当然是有的，而且只要2n+1个，买不了吃亏买不了上当，数学就是这么神奇。首先，我们先找到一系列能代表当前分布的点，称为sigma点，并对应每个点赋予一个权值（想象这些权值和高斯分布中间高两边低对应），记为

点的取法和权值满足（至于为什么这么取$2n+1$个点就行可以参考文献3）

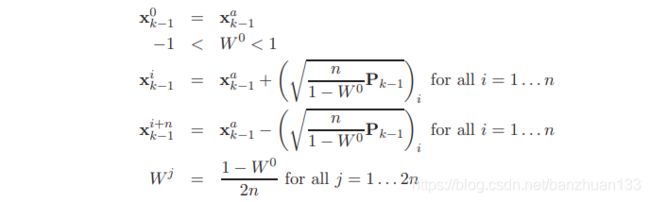
这里$x_{k-1}^a$代表$k-1$时刻的均值（最优估计），$W^0$是一个参数，用来控制sigma点采样的分布，当$W^0>0$时，倾向于采样离均值远的点，反之则倾向于采样较近的点。矩阵的开方根是指
$$A=\sqrt{P},whereA{A}^T=P$$
下标$i$代表第$i$列。接下来的过程就和卡尔曼滤波类似了，首先进行预测，对每个采样点，根据过程模型，有

对应的均值和方差为

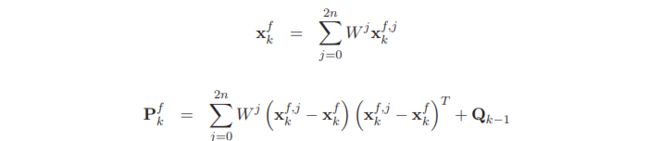
对观测模型，有

对应的均值和方差为

二者的协方差为

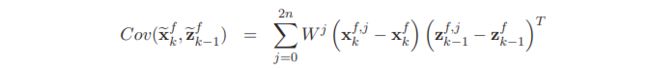
上述过程等价于卡尔曼滤波的预测过程。有了这些结果，当得到k时刻的观测值$z_k$后，我们就可以进行更新过程，类比线性卡尔曼的更新过程，有



同样的，我们用代码复现一下UKF的过程。上面这个过程其实最麻烦的是哪里呢，没错，就是一开始计算权值那里需要用到的矩阵开平方根。计算对称正定阵的方根有不少方法，比较常见的应该是SVD分解和Cholesky分解，MATLAB和Python都有对应的库，这里我们直接利用Python的KalmanFilter库来做（python 真香）

#! /usr/bin/env python
# -*- coding: UTF-8 -*-
import numpy as np
import matplotlib.pyplot as plt
import math
from filterpy.kalman import UnscentedKalmanFilter as UKF
from filterpy.kalman import MerweScaledSigmaPoints
from filterpy.common import Q_discrete_white_noise


dt = 0.1
v = 10

#状态转移矩阵 x, y, theta, v
def transf(x, dt):
    F = np.array([x[0] + math.cos(x[2]) * dt * x[3],
                   x[1] + math.sin(x[2]) * dt * x[3],
                   x[2],
                   x[3]])
    return F.T

# 观测矩阵
def hf(x):
    return np.array([x[3]])


def plot_x(m, ex, zx, x):
    fig = plt.figure(figsize=(16,9))
    plt.plot(range(m),ex, label='$estimateV$')
    plt.plot(range(m),zx, label='$measurementV$')
    plt.axhline(x, color = 'red',label='$trueV$')
    plt.xlabel('Filter Step')
    plt.title('KF Fliter')
    plt.legend(loc='best')
    plt.ylim([5, 15])
    plt.ylabel('Velocity')
    plt.show()

if __name__ == '__main__':
    # 生成sigma点集
    points = MerweScaledSigmaPoints(4, alpha=0.1, beta=2.0, kappa=-1)
    #构造UKF
    ukf = UKF(dim_x = 4, dim_z = 1, fx = transf, hx = hf, dt = dt, points = points)
    # 初始状态赋值
    ukf.x = np.array([0, 0, math.pi/6, 10])
    ukf.P *= 10
    ukf.R = np.diag([0.25])
    ukf.Q = Q_discrete_white_noise(dim=2, dt=dt, var=0.25, block_size=2)

    ukfv = []
    zv = [[ v + np.random.randn()] for i in range(200)]
    for z in zv:
        ukf.predict()
        ukf.update(z)
        ukfv.append(ukf.x.copy())

    ukfv = np.asarray(ukfv)
    plot_x(200, ukfv[:, 3], zv, v)

结果如下

欢迎同步关注我的知乎专栏

参考文献

1. 车辆运动模型 Robin Schubert. Empirical Evaluation of Vehicular Models for Ego Motion Estimation. 2011
2. UKF教程 Unscented Kalman Filter Tutorial
3. 无损变换 S. Julier. The Scaled Unscented Transformation, 1999.
4. 卡尔曼滤波器python库