遗传算法解决旅行商问题(Python版)
完整代码点这里
遗传算法解决旅行商问题(Python版)
一、问题描述
TSP问题(Travelling Salesman Problem)即旅行商问题,又译为旅行推销员问题、货郎担问题,是数学领域中著名问题之一。假设有一个旅行商人要拜访n个城市,他必须选择所要走的路径,路径的限制是每个城市只能拜访一次,而且最后要回到原来出发的城市。路径的选择目标是要求得的路径路程为所有路径之中的最小值。
二、算法描述
2.1算法简介
遗传算法(Genetic Algorithm)是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型,通过模拟自然进化过程搜索最优解。遗传算法是从代表问题可能潜在的解集的一个种群(population)开始的,初代种群产生之后,按照适者生存和优胜劣汰的原理,逐代(generation)演化产生出越来越好的近似解,在每一代,根据问题域中个体的适应度(fitness)大小选择个体,并借助于自然遗传学的遗传算子(genetic operators)进行组合交叉(crossover)和变异(mutation),产生出代表新的解集的种群。这个过程将导致种群像自然进化一样的后生代种群比前代更加适应于环境,末代种群中的最优个体经过解码(decoding),可以作为问题近似最优解。
2.2 遗传算法的实施步骤
第一步:初始化 t←0进化代数计数器;T是最大进化代数;随机生成M个个体作为初始群体P(t);
第二步:个体评价 计算P(t)中各个个体的适应度;
第三步:选择运算 将选择算子作用于群体;
第四步:交叉运算 将交叉算子作用于群体;
第五步:变异运算 将变异算子作用于群体,并通过以上运算得到下一代群体P(t + 1);
第六步:终止条件判断 t≦T:t← t+1 转到步骤2;t>T:终止 输出解。
遗传算法的流程图如下:
三、求解说明
3.1优化目标
给定二维数据int[][]pos用于存储各个城市的坐标,采用欧式距离代表城市之间的距离。利用遗传算法,找到不重复遍历所有城市的路径中,所走距离最短的路径。
3.1选择算子
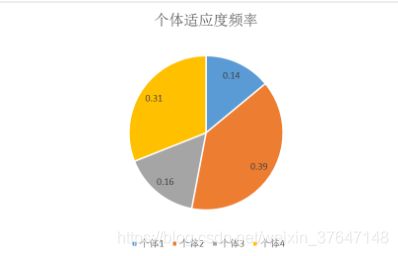
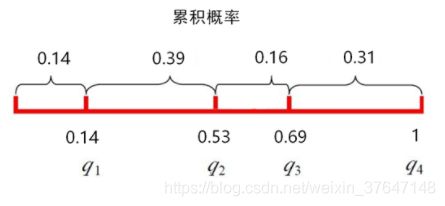
选择算子采用轮盘赌选择,以每个个体的适应度为基础,为每个个体计算累积概率。
个体1、2、3、4的个体适应度如上图所示。
适应度计算规则:染色体代表的路径实际距离作为个体的适应度,如下(distence[x][y]表示城市x到y的距离)
染色体 0 2 1 3,适应度为distence[0][2] + distence[2][1] + distence[1][3] + distence[3][0]
qa 表示个体a的累积概率,如上图所示个体1、2、3、4的累积概率分别为0.14、0.53、0.69、1
随机生成一个0到1的浮点数f,若 qa < f <= qb,则个体b被选中。
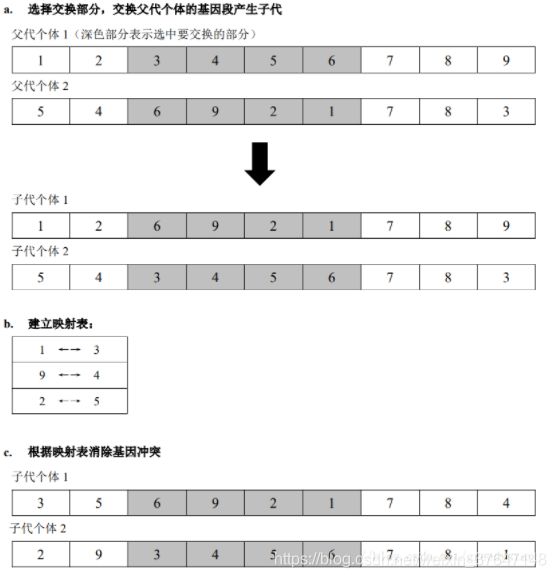
3.2交叉算子
1. Partial-Mapped Crossover(部分映射交叉)
2. Order Crossover(顺序交叉)
3. Position-based Crossover(基于位置的交叉)
3.3 变异算子
变异算子随机进行多次,每次在个体基因序列中选择两个位置的基因进行交换。
3.4 城市路线经纬度
给出中国34个城市的经纬度:
| 编号 |
城市名 |
东经 |
北纬 |
编号 |
城市名 |
东经 |
北纬 |
| 1 |
北京 |
116.46 |
39.92 |
18 |
南京 |
118.78 |
32.04 |
| 2 |
天津 |
117.2 |
39.13 |
19 |
合肥 |
117.27 |
31.86 |
| 3 |
上海 |
121.48 |
31.22 |
20 |
杭州 |
120.19 |
30.26 |
| 4 |
重庆 |
106.54 |
29.59 |
21 |
福州 |
119.3 |
26.08 |
| 5 |
拉萨 |
91.11 |
29.97 |
22 |
南昌 |
115.89 |
28.68 |
| 6 |
乌鲁木齐 |
87.68 |
43.77 |
23 |
长沙 |
113 |
28.21 |
| 7 |
银川 |
106.27 |
38.47 |
24 |
武汉 |
114.31 |
30.52 |
| 8 |
呼和浩特 |
111.65 |
40.82 |
25 |
广州 |
113.23 |
23.16 |
| 9 |
南宁 |
108.33 |
22.84 |
26 |
台北 |
121.5 |
25.05 |
| 10 |
哈尔滨 |
126.63 |
45.75 |
27 |
海口 |
110.35 |
20.02 |
| 11 |
长春 |
125.35 |
43.88 |
28 |
兰州 |
103.73 |
36.03 |
| 12 |
沈阳 |
123.38 |
41.8 |
29 |
西安 |
108.95 |
34.27 |
| 13 |
石家庄 |
114.48 |
38.03 |
30 |
成都 |
104.06 |
30.67 |
| 14 |
太原 |
112.53 |
37.87 |
31 |
贵阳 |
106.71 |
26.57 |
| 15 |
西宁 |
101.74 |
36.56 |
32 |
昆明 |
102.73 |
25.04 |
| 16 |
济南 |
117 |
36.65 |
33 |
香港 |
114.1 |
22.2 |
| 17 |
郑州 |
113.6 |
34.76 |
34 |
澳门 |
113.33 |
22.13 |
3.5 基因编码
n个城市的的基因编码方式为:
- 给每一个城市一个序号,如1->北京,2->上海,3->广州,。。。。,n->成都。
- 用包含n个城市的序号的数组序列表示一种路线(个体),数组元素的序号表示旅行的顺序,如{3, 1, 2,。。。。,n}表示的旅行顺序为:广州->北京->上海->。。。。->成都。
- 数值序列中值不重复,即每个城市只去一次
3.6初始化种群
随机生成m个基因编码序列作为初始种群。
3.7 评估适应度
TSP问题中路线越短越好,适应度取值为总距离的倒数,即1/distance。
3.8 产生新种群
产生新种群分为选择、交叉和变异。个体被选中的概率取决于该个体的适应度值,
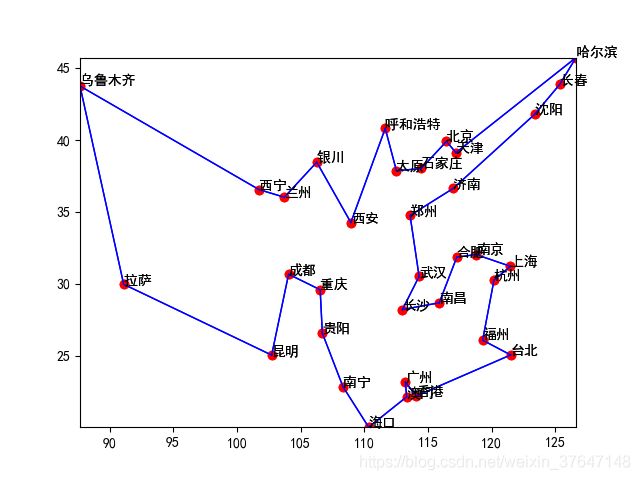
3.9 结果分析
有上图可知,程序经过500次迭代,即34所城市大概迭代500次能收敛到最优。如果继续迭代可能会呈现更好的结果。这里是用中国城市地理坐标直接做欧式距离计算,实际上可以根据问题作出调整。
4.0总结
遗传算法与传统的优化方法相比较,以生物进化为原型,具有很好的收敛性,在计算精度要求时,计算时间少,鲁棒性高等都是它的优点。此外,搜索使用评价函数启发,过程简单。使用概率机制进行迭代,具有随机性。而且具有可扩展性,容易与其他算法结合。缺点是没有能够及时利用网络的反馈信息,故算法的搜索速度比较慢,要得要较精确的解需要较多的训练时间。但是算法对初始种群的选择有一定的依赖性,需要结合一些启发算法进行改进。并且算法的并行机制的潜在能力没有得到充分的利用,这也是当前遗传算法的一个研究热点方向。
四、参考资料
[1] 蔡自兴,王勇. 智能系统原理、算法与应用[M].北京:机械工业出版社,2014
[2] 包子阳,余继周,杨杉编著,智能优化算法及其MATLAB实例(第2版)[M].北京:电子工业出版社,2018.
[3] 黄友锐.智能优化算法及其应用[M].北京:国防工业出版社,2008.
[4] 高海昌,冯博琴.智能优化算法求解TSP问题[J].控制与决策,2006
[5]《群体智能优化算法》专题导语[J].郑州大学学报(工学版),2018.
[6] 王凤娟,姜淑凤,单永瑞,张鹏飞,冉东.群智能优化算法的研究与分析[J].信息通信,2018.
[7] 费腾, 张立毅.现代智能优化算法研究[J].信息技术, 2015.
[8] 李智.智能优化算法研究及应用展望.武汉轻工大学学报, 2016.
[9] 楚东来, 赵伟辰, 林春城.群智能算法的研究现状和发展趋势[J].信息通信, 2015,
[10] https://blog.csdn.net/wangqiuyun/article/details/12838903
[11] https://blog.csdn.net/taonull/article/details/45972393
[12] https://blog.csdn.net/greedystar/article/details/80343841
[13] https://blog.csdn.net/v_JULY_v/article/details/6132775
五、实现代码
本文问题采用Python实现的,核心代码如下: