时间序列预测模型-ARIMA原理及Python实现

1、几个值得参考的链接

https://www.howtoing.com/a-guide-to-time-series-visualization-with-python-3/

https://cloud.tencent.com/developer/article/1480301
https://cloud.tencent.com/developer/article/1038334
https://blog.csdn.net/u014096903/article/details/79980036

 https://wenku.baidu.com/view/1d3e5a89760bf78a6529647d27284b73f24236dd.html
https://www.cnblogs.com/jfdwd/p/9252539.html

https://www.jb51.net/article/158932.htm

推荐下载Anaconda

不建议直接去Python官网下载安装Python，而是去Anaconda官网，下载对应本机操作系统的Anaconda工具。好处有二：

其一，Anaconda是专门用于科学计算的Python发行版，可以很方便地解决多版本Python并存、切换以及各种第三方模块安装的问题。更重要的是，当你下载并安装好Anaconda后，它就已经集成了上百个科学计算的第三方模块，例如numpy,pandas,matplotlib,seaborn,statsmodels,sklearn等。用户需要使用这些模块时，直接导入即可，不用再去下载。

其二，新用户可以使用 Anaconda 发行版来同时安装Python和Jupyter Notebook。Jupyter Notebook 是一个 Web 应用程序，便于创建和共享文学化程序文档，支持实时代码、数学方程、可视化和 Markdown，它提供了一个环境，你可以在其中记录代码，运行代码，查看结果，可视化数据并在查看输出结果。这些特性使其成为一款执行端到端数据科学工作流程的便捷工具 ，可用于数据清理和转换、数值模拟、统计建模、机器学习等等。Jupyter Notebook是Python初学者最好的伙伴和最得力的工具。

注：Jupyter Notebook也可以使用pip 安装方法-这种方法不使用 Anaconda，但需先安装python，并确保机器正在运行最新版本的 pip，之后再安装Jupyter Notebook。相比之下，本人更喜欢前述的直接安装Anaconda方法

转载：https://cloud.tencent.com/developer/article/1430578

Anaconda下载

已安装python3.7的环境基础上，安装Anaconda环境的完整教程

转载：https://blog.csdn.net/qq_36851515/article/details/82956150

本文记录Anaconda完整的下载与安装过程，环境变量的配置，以及如何启动Jupyter notebook并编写第一句代码。以上三项是每一个Python初学者必经之路。。

因为本人电脑是Windows系统，本文仅描述在Windows系统上安装Anaconda的方法，至于Linux和Mac系统，这里不再赘述。

2、代码实现

import pandas as pd
import matplotlib.pylab as plt
from statsmodels.tsa.stattools import adfuller
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
from statsmodels.tsa.arima_model import ARIMA




# 读取数据，pd.read_csv默认生成DataFrame对象，需将其转换成Series对象
df = pd.read_csv('1.csv', encoding='GBK', index_col='date')
df.index = pd.to_datetime(df.index)  # 将字符串索引转换成时间索引
ts = df['people']  # 生成pd.Series对象
print(ts.head())


# 移动平均图
def draw_trend(timeseries, size):
    f = plt.figure(facecolor='white')
    # 对size个数据进行移动平均
    rol_mean = timeseries.rolling(window=size).mean()
    # 对size个数据移动平均的方差
    rol_std = timeseries.rolling(window=size).std()

    timeseries.plot(color='blue', label='Original')
    rol_mean.plot(color='red', label='Rolling Mean')
    rol_std.plot(color='black', label='Rolling standard deviation')
    plt.legend(loc='best')
    plt.title('Rolling Mean & Standard Deviation')
    plt.show()


def draw_ts(timeseries):
    f = plt.figure(facecolor='white')
    timeseries.plot(color='blue')
    plt.show()


# Dickey-Fuller test:
def teststationarity(ts):
    dftest = adfuller(ts)
    # 对上述函数求得的值进行语义描述
    dfoutput = pd.Series(dftest[0:4], index=['Test Statistic', 'p-value', '#Lags Used', 'Number of Observations Used'])
    for key, value in dftest[4].items():
        dfoutput['Critical Value (%s)' % key] = value
    return dfoutput

draw_trend(ts, 7)
# 原始数据、均值、方差
print(teststationarity(ts))
# Dickey-Fuller检验
# ts_log = np.log(ts)
# 对数变换
# ts_log.plot()
# plt.show()
# 查看变换后情况
# print(teststationarity(ts_log))
# Dickey-Fuller检验
# 移动平均
def draw_moving(timeSeries, size):
    f = plt.figure(facecolor='white')
    # 对size个数据进行移动平均
    rol_mean = timeSeries.rolling(window=size).mean()
    # 对size个数据进行加权移动平均
    rol_weighted_mean = pd.DataFrame(timeSeries).ewm(span=size).mean()
    # rol_weighted_mean=timeSeries.ewm(halflife=size,min_periods=0,adjust=True,ignore_na=False).mean()

    timeSeries.plot(color='blue', label='Original')
    rol_mean.plot(color='red', label='Rolling Mean')
    rol_weighted_mean.plot(color='black', label='Weighted Rolling Mean')
    plt.legend(loc='best')
    plt.title('Rolling Mean')
    plt.show()


draw_moving(ts, 7)
# 窗口为7的移动平均，剔除周期性因素，再对周期内数据进行加权，一定程度上减小周期因素
diff_7 = ts.diff(7)
diff_7.dropna(inplace=True)
print(teststationarity(diff_7))
diff_7_1 = diff_7.diff(1)
diff_7_1.dropna(inplace=True)
# 以上为差分
print(teststationarity(diff_7_1))
# Dickey-Fuller检验
# 预测
rol_mean = ts.rolling(window=7).mean()
rol_mean.dropna(inplace=True)
ts_diff_1 = rol_mean.diff(1)
ts_diff_1.dropna(inplace=True)
print(teststationarity(ts_diff_1))
# 二阶差分
ts_diff_2 = ts_diff_1.diff(1)
ts_diff_2.dropna(inplace=True)
print(teststationarity(ts_diff_2))

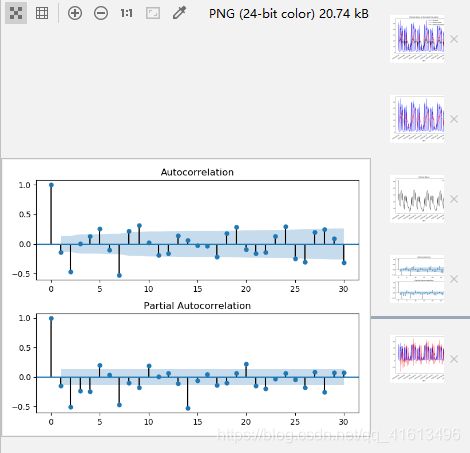
# 画出ACF、PACF图
def draw_acf_pacf(ts,lags):
    f = plt.figure(facecolor='white')
    ax1 = f.add_subplot(211)
    plot_acf(ts,ax=ax1,lags=lags)
    ax2 = f.add_subplot(212)
    plot_pacf(ts,ax=ax2,lags=lags)
    plt.subplots_adjust(hspace=0.5)
    plt.show()

# 画出2阶差分后的ACF、PACF图.PACF-p,ACF-q
draw_acf_pacf(ts_diff_2, 30)


# 拟合模型
model = ARIMA(ts_diff_1, order=(1, 1, 1))
result_arima = model.fit( disp=-1, method='css')


# 以下为数据还原
predict_ts = result_arima.predict()
# 一阶差分还原
diff_shift_ts = ts_diff_1.shift(1)
diff_recover_1 = predict_ts.add(diff_shift_ts)
# 再次一阶差分还原
rol_shift_ts = rol_mean.shift(1)
diff_recover = diff_recover_1.add(rol_shift_ts)
# 移动平均还原
rol_sum = ts.rolling(window=6).sum()
rol_recover = diff_recover*7 - rol_sum.shift(1)
# 对数还原
# log_recover = np.exp(rol_recover)
# log_recover.dropna(inplace=True)
# log_recover.plot()
# plt.show()


# 使用均方根误差（RMSE）评估模型拟合好坏。利用该准则进行判别时需要剔除“非预测”数据的影响
rol_recover.plot(color='red', label='Predict')
ts.plot(color='blue', label='Original')
plt.show()

本人是以对数据集（日期|星期几|来访人数）进行预测

实现效果：