吴恩达机器学习课后作业_线性回归实现

照着bilibili上，一位小姐姐?的ng机器学习课后作业系列视频，细节讲的真的很到位，get到了很多基础知识。传送门

---

目录
一、单变量线性回归
二、多变量线性回归

---

1单变量线性回归

根据城市的人口数量，预测获利情况。

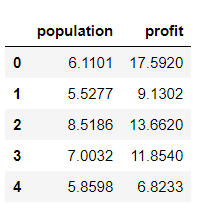
1、加载数据集

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline

data = pd.read_csv('./ex1data1.txt', names=['population', 'profit'])   
# names=['population', 'profit'] 给数据集的列添加标题

# 查看数据信息
data.head() # 前5行
# print(data.tail())  # 最后5行
# print(data.describe())  # 方差、均值等统计
# print(data.info())  # 信息

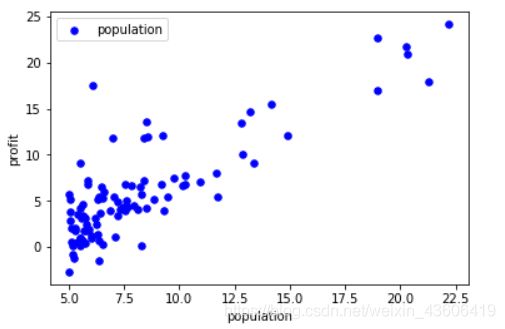
# 可视化数据集
data.plot.scatter('population', 'profit', c='b', label='population', s=30)   
# 颜色为蓝色、s代表样本点的大小
plt.show()

知识点补充1：

知识点补充2：

2、构造数据集

# 加入特征列 x0 = 1
data.insert(0, 'ones', 1)  # 要插入的位置，标签（字符串），数值
# print(data.head())

# 获取特征与标签
x = data.iloc[:, 0:-1]
# print(x.head())

# print(type(x))
# 

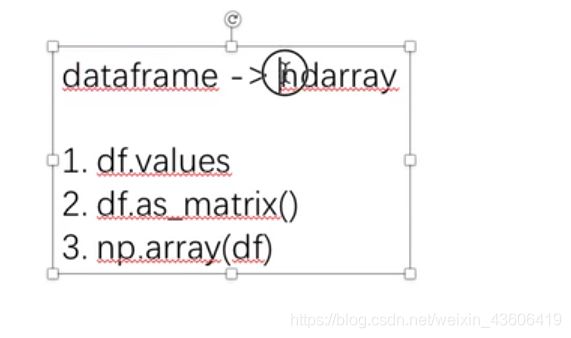
x = x.values   # 类型转换，便于用numpy计算

# print(type(x))
# 
# print(len(x))
# print(x.shape)  # (97, 2)

y = data.iloc[:, -1].values
# print(y.shape)  # (97,)  一维数组
y = y.reshape(-1, 1)
# print(y.shape)  # (97, 1)  二维数组，很重要

3. 损失函数

def costFunction(x, y, theta):
    inner = np.power(x @ theta - y, 2)  # 矩阵相乘 @ 或者用np.dot(a, b)
    return np.sum(inner) / (2 * len(x))
    
# 初始化参数为0
theta = np.zeros((2, 1))      # (97, 2)  *  (2, 1)  =  （97,1）

# 计算初始的代价函数
cost_init = costFunction(x, y, theta)
print(cost_init)

运行结果：
32.072733877455676

4. 梯度下降

def tD(x, y, theta, al, iters, is_plot=False):

    costs =[]  # 存放每一次迭代的cost值
    for i in range(iters):
        theta = theta - al/len(x) * (x.T @ (x @ theta - y))
        cost = costFunction(x, y, theta)
        costs.append(cost)

        if i % 100 == 0:
            if is_plot:
                print(cost)

    return theta, costs

5 可视化梯度下降

# 学习率
al = 0.02  

# 迭代次数
iters = 2000

fig, ax = plt.subplots()   
# fig 表示整个图  
# ax表示实例化的对象

theta_final, costs = tD(x, y, theta, al, iters)

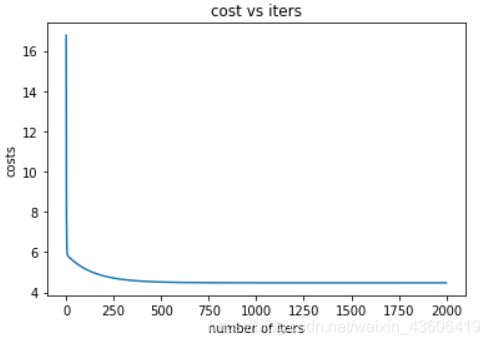
# 6、可视化 损失函数
ax.plot(np.arange(iters), costs)

ax.set(xlabel='number of iters',
       ylabel='costs',
       title='cost vs iters')
plt.show()

补充知识点3：
如图，fig代表整个图，ax代表实例化的对象，ax1为左上角ax[0,0]

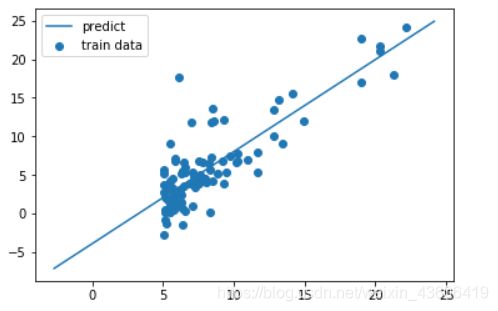
6 拟合情况可视化

a = np.linspace(y.min(), y.max(), 100)
# 利用得到的最优参数，拟合曲线
y_pred = theta_final[0, 0] + theta_final[1, 0] * a    

fig, ax = plt.subplots()
# 真实样本
ax.scatter(x[:, 1], y, label='train data')
# 预测结果
ax.plot(a, y_pred, label='predict')
ax.legend()
plt.show()

---

2 多变量线性回归

两个特征 sizes、bedrooms，预测 price of house

1、加载数据集

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline

data = pd.read_csv('./ex1data2.txt', names=['sizes', 'bedrooms', 'prices'])
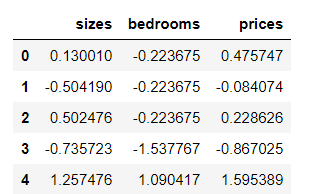
data.head()

2、数据标准化

data = (data - data.mean()) / data.std()  
#  对每一列求均值、标准差
data.head()

3、构造数据集

# 添加一列，作为 特征x0，对应 参数theta0
data.insert(0,'ones',1) # 添加列的位置（最左边） 添加的列的名字（字符串 ones） 参加的值 1
data.head()

# 提取特征与标签
X = data.iloc[:, 0:-1]
y = data.iloc[:, -1]

X = X.values
y = y.values
type(y)
print(X.shape)
print(y.shape)

(47, 3)
(47,)

4. 损失函数

# 损失函数
def cost_function(X, y, theta):
    inner = np.power(X @ theta - y, 2)
    return np.sum(inner) / (2 * len(X))

# 初始化 tehta0 tehta1
theta = np.zeros((3,1))
cost_init = cost_function(X, y, theta)
cost_init

5. 梯度下降

# 梯度下降
def tD(X, y, theta, al, iters, is_plot=False):

    costs =[]  # 利用 costs 可视化
    for i in range(iters):
        theta = theta - al/len(X) * (X.T @ (X @ theta - y))
        cost = cost_function(X, y, theta)
        costs.append(cost)

        if i % 100 == 0:
            if is_plot:
                print(cost)

    return theta, costs

6.不同学习率对比

n_al = [0.003, 0.03, 0.001, 0.01]
iters = 2000

fig, ax = plt.subplots()
for al in n_al:
    theta_final, costs = tD(X, y, theta, al, iters)

    ax.plot(np.arange(iters), costs, label=al)
    ax.legend()
    
ax.set(xlabel='number of iters',
       ylabel='costs',
       title='cost vs iters')
plt.show()