吴恩达机器学习——线性回归
文章目录
- 前言
- 一、单变量线性回归
-
- 单位矩阵
- 代价函数
- 寻找全局最小值
- 二、多变量线性回归
-
- 特征标准化
- 寻找全局最小值
前言
自己从前段时间开始学习机器学习的相关知识,看了一些经典的书籍,但书上讲的总归有些晦涩,看到大家在推荐吴恩达的课程,于是去看了,发现确实很不错,有很多书上难懂的公式,其实视频里十几分钟就讲明白了,效率很高。这个博客会作为一个系列,用来讲解自己做的编程练习题,为同样正在入门的同学提供一些思路,也为自己做一个备忘。这个系列文章不会讲解课程视频中已经出现的知识点,这就有点工作量太大了,也不会出现绘图等相关性不大的东西。一切以课后练习为主。
一、单变量线性回归
该测试对应于文件ex1。
单位矩阵
该文件对应的是warmUpExercise.m文件,目的是使用matlab生成单位矩阵。单位矩阵是从左上角到右下角这条线上的元素全为0,其他元素都为0,且行数列数相等的矩阵,matlab中使用eye()函数来生成单位矩阵。

代价函数
该文件对应computeCost.m文件。函数原型为computeCost(X, y, theta),X是样本的横坐标,y是样本的纵坐标。theta则是我们最终要求出的参数。
单变量线性回归我们知道就是求一条直线,使得该直线能够准确地沿着样本的分布。这条直线的方程显然就是一个一元一次方程:
y = θ 1 + θ 2 ∗ x y = \theta_{1} + \theta_{2}*x y=θ1+θ2∗x
此处我们首先按照标量的方式来看这个公式。后面为了计算方便,有时候会直接使用矩阵运算来进行,到时候要按照传入的x和theta形式来灵活修改。
OK,先明确一下目的,以往我们的目标是放眼在x和y上,但这里我们的目标是找到一条直线,也就是theta1和theta2,来使得训练集中所有的点距离这条直线的距离总和最短。
那么显然的,我们的公式应该如下所示:
c o s t = 1 2 m ∑ i = 1 m ( θ 1 + θ 2 x i − y i ) 2 cost=\frac{1}{2m}\sum_{i=1}^{m}(\theta_{1} + \theta_{2}x_{i} - y_{i})^2 cost=2m1i=1∑m(θ1+θ2xi−yi)2
其中,m是样本数量。在测试中,X是一个m行1列的矩阵,y也是同样。
X = [ x 1 x 2 . . . x m ] \bm{X}=\begin{bmatrix}x_{1}\\x_{2}\\...\\x_{m}\end{bmatrix} X=⎣⎢⎢⎡x1x2...xm⎦⎥⎥⎤
y = [ y 1 y 2 . . . y m ] \bm{y}=\begin{bmatrix}y_{1}\\y_{2}\\...\\y_{m}\end{bmatrix} y=⎣⎢⎢⎡y1y2...ym⎦⎥⎥⎤
而theta则是一个1行2列的矩阵。
θ = [ θ 1 θ 2 ] \bm{\theta}=\begin{bmatrix}\theta_{1}\\\theta_{2}\\\end{bmatrix} θ=[θ1θ2]
由于我们使用matlab,不能按照平时写代码的思路去考虑矩阵计算。最方便的就是使用matlab强大的数学计算功能(不得不说有时候太强了反而不是很容易用)。为了使用简便的矩阵运算,测试文件中为X添加了一列全是1,即传入函数的X的形式是
X = [ 1 x 1 1 x 2 . . . . . . 1 x m ] \bm{X}=\begin{bmatrix}1&x_{1}\\1&x_{2}\\...&...\\1&x_{m}\end{bmatrix} X=⎣⎢⎢⎡11...1x1x2...xm⎦⎥⎥⎤
如此我们可以得出
X ∗ θ − y = [ θ 1 + θ 2 x 1 − y 1 θ 1 + θ 2 x 2 − y 2 . . . θ 1 + θ 2 x m − y m ] \bm{X*\theta-y}=\begin{bmatrix}\theta_{1} + \theta_{2}x_{1} - y_{1}\\\theta_{1} + \theta_{2}x_{2} - y_{2}\\...\\\theta_{1} + \theta_{2}x_{m} - y_{m}\end{bmatrix} X∗θ−y=⎣⎢⎢⎡θ1+θ2x1−y1θ1+θ2x2−y2...θ1+θ2xm−ym⎦⎥⎥⎤
如此,我们将这些转换为matlab代码,其实就两行
d = y - X * theta;
J = sum(d .* d) / (2 * m);
d就是我们的式1,由于最终需要平方,所以谁减谁都无所谓,但是矩阵的乘法顺序不能搞错,因为矩阵运算不满足交换律。
对于平方,我直接使用了点乘,当然矩阵平方是可以使用d.^2这样的形式。最终的J就是我们计算出的代价。
寻找全局最小值
我们最终的目的是使得cost最小。寻找全局最小值的函数就是gradientDescent(X, y, theta, alpha, num_iters),alpha是我们的步进大小,num_iters则是我们总共计算的步数。X、y、theta的形式都和上面相同。
课程中已经讲过,寻找全局最小值就是沿着 θ 1 \theta_{1} θ1和 θ 2 \theta_{2} θ2下降的方向进行寻找。那么自然免不了要对 θ 1 \theta_{1} θ1和 θ 2 \theta_{2} θ2进行求导。
为了方便理解,这次我们按照测试文件中X的形式表达cost,即X的第一列全是1。
c o s t = 1 2 m ∑ i = 1 m ( θ 1 x i 1 + θ 2 x i 2 − y i ) 2 cost=\frac{1}{2m}\sum_{i=1}^{m}(\theta_{1}x_{i1} + \theta_{2}x_{i2} - y_{i})^2 cost=2m1i=1∑m(θ1xi1+θ2xi2−yi)2
x i j x_{ij} xij表示矩阵中第i行第j列的元素,显然, x i 1 x_{i1} xi1都是1。
d c o s t d θ 1 = 1 m ∑ i = 1 m ( θ 1 x i 1 + θ 2 x i 2 − y i ) x i 1 \frac{d\bm{cost}}{d\bm{\theta_{1}}}=\frac{1}{m}\sum_{i=1}^{m}(\theta_{1}x_{i1} + \theta_{2}x_{i2} - y_{i})x_{i1} dθ1dcost=m1i=1∑m(θ1xi1+θ2xi2−yi)xi1
d c o s t d θ 2 = 1 m ∑ i = 1 m ( θ 1 x i 1 + θ 2 x i 2 − y i ) x i 2 \frac{d\bm{cost}}{d\bm{\theta_{2}}}=\frac{1}{m}\sum_{i=1}^{m}(\theta_{1}x_{i1} + \theta_{2}x_{i2} - y_{i})x_{i2} dθ2dcost=m1i=1∑m(θ1xi1+θ2xi2−yi)xi2
据此
d c o s t d θ j = 1 m ∑ i = 1 m ( θ 1 x i 1 + θ 2 x i 2 − y i ) x i j \frac{d\bm{cost}}{d\bm{\theta_{j}}}=\frac{1}{m}\sum_{i=1}^{m}(\theta_{1}x_{i1} + \theta_{2}x_{i2} - y_{i})x_{ij} dθjdcost=m1i=1∑m(θ1xi1+θ2xi2−yi)xij
求导已经搞清楚了,接下来就是更新 θ 1 \theta_{1} θ1和 θ 2 \theta_{2} θ2的方法,课程视频中已经讲过。
t e m p = θ − α ∗ d c o s t d θ temp=\theta-\alpha*\frac{d\bm{cost}}{d\bm{\theta}} temp=θ−α∗dθdcost
θ = t e m p \theta=temp θ=temp
为什么要使用temp这个临时变量呢?因为我们这里有两个值需要更新,你在更新后一个的时候要保证导数的式子不能变,不然求的就不是那个点的导数。也就是
t e m p 1 = θ 1 − α ∗ d c o s t d θ 1 temp1=\theta_{1}-\alpha*\frac{d\bm{cost}}{d\bm{\theta_{1}}} temp1=θ1−α∗dθ1dcost
t e m p 2 = θ 2 − α ∗ d c o s t d θ 2 temp2=\theta_{2}-\alpha*\frac{d\bm{cost}}{d\bm{\theta_{2}}} temp2=θ2−α∗dθ2dcost
θ 1 = t e m p 1 \theta_{1}=temp1 θ1=temp1
θ 2 = t e m p 2 \theta_{2}=temp2 θ2=temp2
综合上面所有式子,写成matlab代码就是
m = length(y); % number of training examples
J_history = zeros(num_iters, 1);
for iter = 1:num_iters
% ====================== YOUR CODE HERE ======================
% Instructions: Perform a single gradient step on the parameter vector
% theta.
%
% Hint: While debugging, it can be useful to print out the values
% of the cost function (computeCost) and gradient here.
%
temp0 = theta(1) - alpha * sum((X * theta - y) .* X(:,1)) / m;
temp1 = theta(2) - alpha * sum((X * theta - y) .* X(:,2)) / m;
theta(1) = temp0;
theta(2) = temp1;
% ============================================================
% Save the cost J in every iteration
J_history(iter) = computeCost(X, y, theta);
end
这是函数体。
稍微解释下alpha * sum((X * theta - y) .* X(:,1))。我们已经知道X * theta - y就是一个m行1列的矩阵,上面求d的操作已经说过。然后只要对X中的对应元素进行点乘即可。
( X ∗ θ − y ) . ∗ X ( : , j ) = [ ( θ 1 x 11 + θ 2 x 12 − y i ) x 1 j ( θ 1 x 21 + θ 2 x 22 − y i ) x 2 j ( θ 1 x 31 + θ 2 x 32 − y i ) x 3 j . . . ( θ 1 x m 1 + θ 2 x m 2 − y i ) x m j ] \bm{(X*\theta-y).*X(:,j)}= \begin{bmatrix} (\theta_{1}x_{11} + \theta_{2}x_{12} - y_{i})x_{1j}\\ (\theta_{1}x_{21} + \theta_{2}x_{22} - y_{i})x_{2j}\\ (\theta_{1}x_{31} + \theta_{2}x_{32} - y_{i})x_{3j}\\ ...\\ (\theta_{1}x_{m1} + \theta_{2}x_{m2} - y_{i})x_{mj} \end{bmatrix} (X∗θ−y).∗X(:,j)=⎣⎢⎢⎢⎢⎡(θ1x11+θ2x12−yi)x1j(θ1x21+θ2x22−yi)x2j(θ1x31+θ2x32−yi)x3j...(θ1xm1+θ2xm2−yi)xmj⎦⎥⎥⎥⎥⎤
最后sum()这个函数在这里是求这个m行1列中所有元素之和。更多用法可在matlab中输入help sum获取帮助。
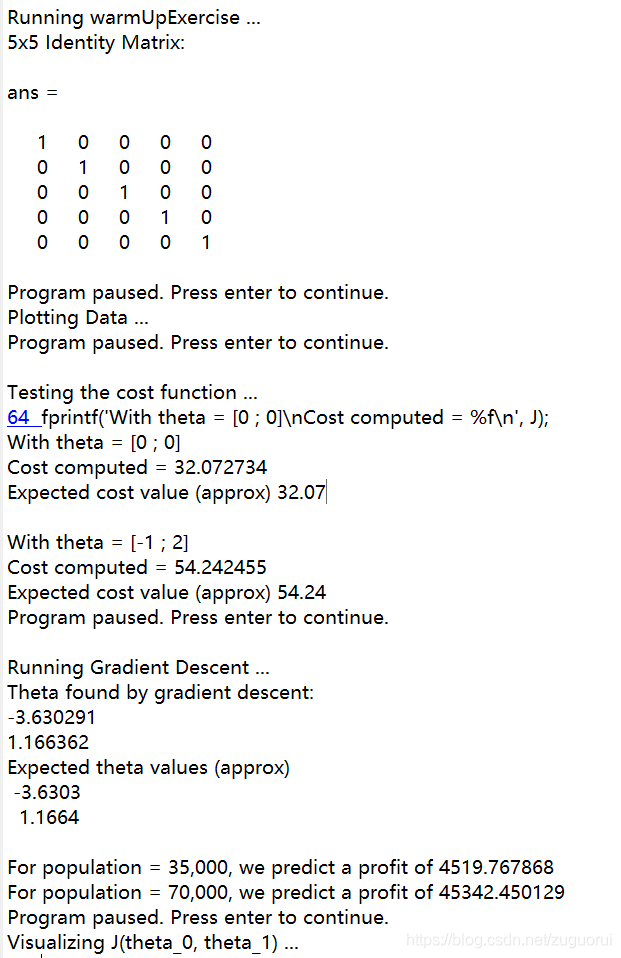
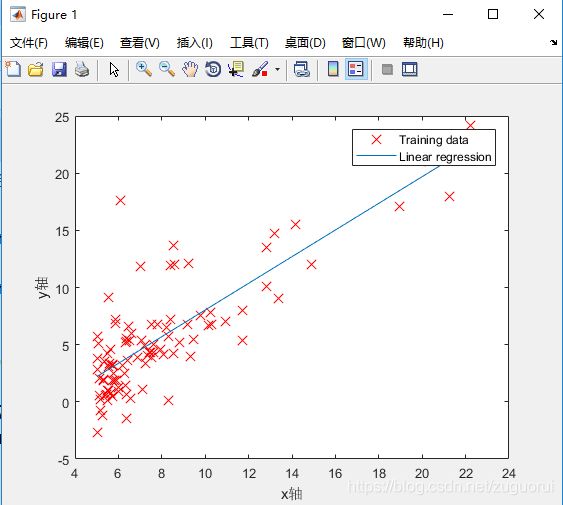
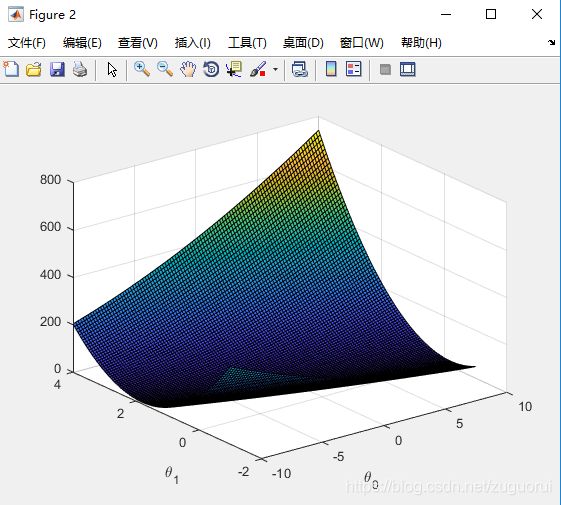
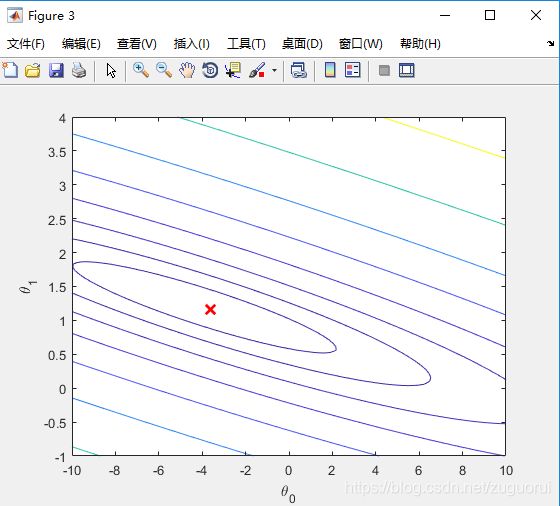
到这里,单变量线性回归我们已经完成了,运行ex1.m即可得到结果。
二、多变量线性回归
该测试对应的是ex1_multi.m。
特征标准化
特征标准化的意义在于使得特征处于一个数量级上,这样计算出来的参数更加准确。该函数是[X_norm, mu, sigma] = featureNormalize(X),其中X_norm是标准化后的矩阵,它每一行是一个样本,列对应的是样本特征。mu是特征对应的均值。sigma则是标准差。其实这个代码很简单,就直接上了。
X_norm = X;
mu = zeros(1, size(X, 2));
sigma = zeros(1, size(X, 2));
len = size(X, 2);
for i = 1:len
m = mean(X_norm(:, i));
X_norm(:, i) = X_norm(:, i) - m;
s = std(X_norm(:, i));
X_norm(:, i) = X_norm(:, i) / s;
mu(i) = m;
sigma(i) = s;
end
size(X, 2)返回的是列数,size(X, 1)返回的是行数。
寻找全局最小值
该函数是[theta, J_history] = gradientDescentMulti(X, y, theta, alpha, num_iters),其实和我们之前用的单变量的差不多。只不过在那个版本中,我们默认了 θ \bm{\theta} θ有两个值,而 X \bm{X} X仅有一个特征。在这里我们要灵活应对 X \bm{X} X的特征数量,也就是只要用循环或者干脆直接使用矩阵计算即可。思路和前面的一样,直接上代码。
m = length(y); % number of training examples
w = size(X, 2);
J_history = zeros(num_iters, 1);
temp = zeros(1, size(theta, 1));
for iter = 1:num_iters
for i = 1:w
temp(i) = theta(i) - alpha * sum((X * theta - y) .* X(:,i)) / m;
end
for i = 1:w
theta(i) = temp(i);
end
% Save the cost J in every iteration
J_history(iter) = computeCostMulti(X, y, theta);
end
需要注意的是我们要在part2和part3中修改一些代码,来验证结果。在part2中由于我们使用了标准化,因此要考虑到这一点。
part2:
% Estimate the price of a 1650 sq-ft, 3 br house
% ====================== YOUR CODE HERE ======================
% Recall that the first column of X is all-ones. Thus, it does
% not need to be normalized.
price = 0; % You should change this
x_t = [1, 1650, 3];
for i = 2:3
x_t(i) = x_t(i) - mu(i - 1);
x_t(i) = x_t(i) / sigma(i - 1);
end
price = x_t * theta;
part3:
% Estimate the price of a 1650 sq-ft, 3 br house
% ====================== YOUR CODE HERE ======================
x_t = [1, 1650, 3];
price = 0; % You should change this
price = x_t * theta;
最后运行即可看到结果。