线性回归—投资额(python、OLS最小二乘、残差图、DW检验)
线性回归—投资额(python、OLS最小二乘、残差图、DW检验)
一、问题描述:
建立投资额模型,研究某地区实际投资额与国民生产值(GNP)及物价指数(PI)的关系,根据对未来GNP及PI的估计,预测未来投资额。以下是该地区连续20年的统计数据。
| 年份序号 | 投资额 | 国民生产总值 | 物价指数 |
| 1 | 90.9 | 596.7 | 0.7167 |
| 2 | 97.4 | 637.7 | 0.7277 |
| 3 | 113.5 | 691.1 | 0.7436 |
| 4 | 125.7 | 756 | 0.7676 |
| 5 | 122.8 | 799 | 0.7906 |
| 6 | 133.3 | 873.4 | 0.8254 |
| 7 | 149.3 | 944 | 0.8679 |
| 8 | 144.2 | 992.7 | 0.9145 |
| 9 | 166.4 | 1077.6 | 0.9601 |
| 10 | 195 | 1185.9 | 1.0000 |
| 11 | 229.8 | 1326.4 | 1.0575 |
| 12 | 228.7 | 1434.2 | 1.1508 |
| 13 | 206.1 | 1594.2 | 1.2579 |
| 14 | 257.9 | 1718 | 1.3234 |
| 15 | 324.1 | 1918.3 | 1.4005 |
| 16 | 386.6 | 2163.9 | 1.5042 |
| 17 | 423 | 2417.8 | 1.6342 |
| 18 | 401.9 | 2631.7 | 1.7842 |
| 19 | 474.9 | 2954.7 | 1.9514 |
| 20 | 424.5 | 3073 | 2.0688 |
二、问题分析:
以时间为序的数据称为时间序列。时间序列中同一变量的顺序观测值之间存在自相关,若采用普通回归模型直接处理,将会出现不良后果。因此,需要诊断并消除数据的自相关性,建立新的模型。另外许多经济数据在时间上有一定的滞后性,也会影响模型效果。
本文按照正常建模流程来处理数据,分析每个模型的优缺点并进行比较。
三、基本模型:
变量描述:
t t t~年份序号
y t y_{t} yt~投资额
x 1 t x_{1t} x1t~GNP
x 2 t x_{2t} x2t~物价指数
画散点图:
拿到数据的第一步,画散点图,观察投资额与GNP和物价指数的基本关系。

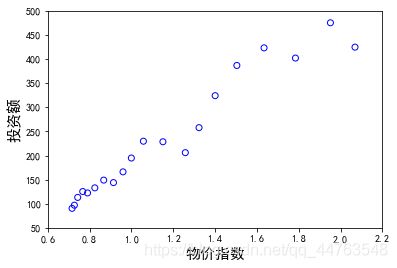
可以看到,投资额与GNP及物价指数间均有很强的线性关系。所以,构建基本回归模型:
y t = β 0 + β 1 x 1 t + β 2 x 2 t + ϵ t y_{t} = \beta_{0}+\beta_{1}x_{1t}+\beta_{2}x_{2t}+\epsilon_{t} yt=β0+β1x1t+β2x2t+ϵt
四、模型求解和代码展示:
第一步,导入相关库,并解决画图中文问题。
#导入库
import cmath
import numpy as np
import pandas as pd
import statsmodels.api as sm
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus'] = False
#matplotlib画图中中文显示会有问题,需要这两行设置默认字体
第二步,导入数据,变量描述。
#导入数据
touzi = pd.read_csv("touzi.csv")
touzi = pd.DataFrame(touzi)
#变量描述
t = touzi['年份序号']
yt = touzi['投资额']
x1t = touzi['国民生产总值']
x2t = touzi['物价指数']
第三步,分析 y t y_{t} yt(投资额) 和 x 1 t x_{1t} x1t(GNP)及 x 2 t x_{2t} x2t(物价指数) 之间的关系,通过散点图得以直观表达。分别是图1、图2。
第四步(最重要一步),求解模型回归系数: β 0 、 β 1 、 β 2 \beta_{0}、\beta_{1}、\beta_{2} β0、β1、β2.
本文用OLS普通最小二乘法求解,在下列代码 (‘yt ~ x1t + x2t’, data = touzi)中,yt表示因变量。自变量则在yt~后边表示成变量相加的格式,模型会自动求解出变量前的回归系数。
#yt = b0 + b1x1t + b2x2t + e
model_1 = sm.formula.ols('yt ~ x1t + x2t', data = touzi).fit() #OLS普通最小二乘法
model_1.summary()

下面是模型结果中部分参数的解释。
左边:
Dep.Variable: 输出变量的名称
Model: 模型名称
Method: 方法,其中 Least Squares 表示最小二乘法
Date: 日期
Time: 时间
No.Observations: 样本数目
Df Residuals: 残差自由度
Df Model: 模型参数个数,相当于输入的X的元素个数
右边:
R- squared: 可决系数,用来判断估计的准确性,范围在[0,1]越接近1,说明对y的解释能力越强,拟合越好
Adj-R- squared: 通过样本数量与模型数量对R-squared进行修正,奥卡姆剃刀原理,避免描述冗杂
F-statistic: 衡量拟合的显著性,重要程度
Prob(F-statistic): 当prob(F-statistic)<α时,表示拒绝原假设,即认为模型是显著的
Log likelihood: 对数似然比LLR
AIC: 衡量拟合优良性
BIC: 贝叶斯信息准则
主要看此处的结果。Intercept表示 β 0 \beta_{0} β0 的数值, x 1 t 、 x 2 t x_{1t}、x_{2t} x1t、x2t分别表示求得自身系数 β 1 、 β 2 \beta_{1}、\beta_{2} β1、β2 的数值。
coef: 系数
std err: 系数估计的基本标准误差
t: t统计值,衡量系数统计显著程度的指标
P>|t|: P值
[0.025,0.975]: 95%置信区间的下限和上限值
五、基本回归模型结果分析:
equation_yt = 'yt方程为:' + '\tyt' + ' = ' + '363.7029' + ' + ' + '0.6792' + '*x1t ' + '- ' + '972.7857' + '*x2t'
print(equation_yt)
pre_yt = 363.7029 + 0.6792*x1t - 972.7857*x2t
pre_yt = list(pre_yt)
MSE = cmath.sqrt(sum((yt - pre_yt)**2/(20)))
print('剩余标准差:\ts = ',MSE)
print('R2 = ',0.990,',拟合度高')
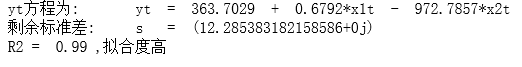
模型优点: R 2 = 0.990 R^2 = 0.990 R2=0.990,拟合度高
模型缺点:没有考虑时间序列数据的滞后性影响,可能忽视了随机误差存在自相关,如果存在自相关,用此模型会有不良后果。
六、自相关的定性诊断:
1、残差诊断法
模型残差 e t = y t − y ^ t e_{t} = y_{t} -\widehat{y}_{t} et=yt−y t
e t e_{t} et为随机误差 ϵ t \epsilon_{t} ϵt的估计值。
作残差 e t e_{t} et~ e t − 1 e_{t-1} et−1散点图,如果大部分点落在第1,3象限,则 ϵ t \epsilon_{t} ϵt存在正的自相关;如果大部分点落在第2,4象限,则 ϵ t \epsilon_{t} ϵt存在负的自相关。
#残差诊断法
et = yt - pre_yt #残差
et = list(et)
#残差et 与 et_1 散点图
plt.ylim(-30, 20)
plt.xlim(-30, 20)
plt.plot([-30,20],[0,0],'b',linewidth=1)
plt.plot([0,0],[-30,20],'b',linewidth=1)
et_1 = et[1:20]
et_change = et[0:19]
plt.scatter(et_1,et_change,marker = '+',color = 'g')

自相关直观判断,基本回归模型的随机误差 ϵ t \epsilon_{t} ϵt存在正的自相关。注:此图不能直观看出大部分点落在第1,3象限,与案例中的图不太相同,不知原因,如有解决的朋友欢迎在评论区留言。下面展示案例图:

D W = ∑ t = 2 n ( e t − e t − 1 ) 2 ∑ t = 2 n e t 2 ≈ 2 [ 1 − ∑ t = 2 n e t e t − 1 ∑ t = 2 n e t 2 ] = 2 ( 1 − ρ ^ ) DW{\rm{ = }}\frac{ {\sum\limits_{t = 2}^n { { {({e_t} - {e_{t - 1}})}^2}} }}{ {\sum\limits_{t = 2}^n {e_t^2} }} \approx 2[1 - \frac{ {\sum\limits_{t = 2}^n { {e_t}{e_{t - 1}}} }}{ {\sum\limits_{t = 2}^n {e_t^2} }}] = 2(1-\widehat{\rho}) DW=t=2∑net2t=2∑n(et−et−1)2≈2[1−t=2∑net2t=2∑netet−1]=2(1−ρ )
其中, ρ ^ = ∑ t = 2 n e t e t − 1 ∑ t = 2 n e t 2 \widehat{\rho} = \frac{ {\sum\limits_{t = 2}^n { {e_t}{e_{t - 1}}} }}{ {\sum\limits_{t = 2}^n {e_t^2} }} ρ =t=2∑net2t=2∑netet−1,此处 ≈ \approx ≈的前提是 n n n较大。
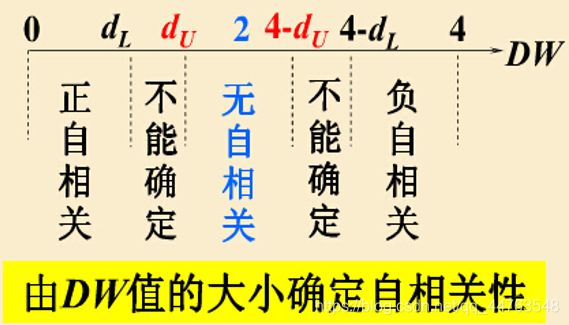
其中, d L d_{L} dL和 d U d_{U} dU需要查询D-W分布表。 − 1 -1 −1 ≤ \le ≤ ρ ^ \widehat{\rho} ρ ≤ \le ≤ 1 1 1 即 0 0 0 ≤ \le ≤ D W DW DW ≤ \le ≤ 4 4 4 .
注:以下DW计算数据均用课件给出数据,不再计算,有兴趣的朋友可以计算,因为用最小二乘估计参数与课件数据有偏差,计算出来的DW值不符合正自相关性,如果我解决了会及时修改。不过程序计算步骤都是没有问题的。
D W DW DW计算程序:
#D-W统计量
DW = sum([(m-n)**2 for m,n in zip(et_change,et_1)])/sum([m**2 for m in et_change])
print('DW =',DW,' 解释:因误差,假设原模型有正自相关')
p = 1-DW/2
print('p =',p)
原模型 D W o l d = 0.8754 DW_{old}=0.8754 DWold=0.8754,根据样本容量 n = 20 n=20 n=20, α = 0.05 \alpha=0.05 α=0.05,通过查表得到 d L = 1.10 d_{L}=1.10 dL=1.10, d U = 1.54 d_{U}=1.54 dU=1.54,因为 D W o l d < d L DW_{old}
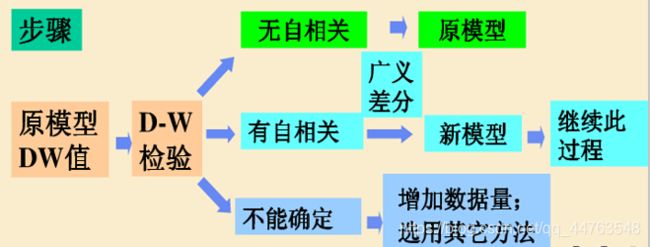
七、广义差分变换:
原模型: y t = β 0 + β 1 x 1 t + β 2 x 2 t + ε t , ε t = ρ ε t − 1 + u t y_{t}=\beta_{0}+\beta_{1} x_{1 t}+\beta_{2} x_{2 t}+\varepsilon_{t}, \quad\varepsilon_{t}=\rho \varepsilon_{t-1}+u_{t} yt=β0+β1x1t+β2x2t+εt,εt=ρεt−1+ut
变换: y t ∗ = y t − ρ y t − 1 , x i t ∗ = x i t − ρ x i , t − 1 , i = 1 , 2 y_{t}^{*}=y_{t}-\rho y_{t-1}, x_{i t}^{*}=x_{i t}-\rho x_{i, t-1},\quad i=1,2 yt∗=yt−ρyt−1,xit∗=xit−ρxi,t−1,i=1,2
新模型: y t ∗ = β 0 ∗ + β 1 x 1 t ∗ + β 2 x 2 t ∗ + u t , β 0 ∗ = β 0 ( 1 − ρ ) y_{t}^{*}=\beta_{0}^{*}+\beta_{1} x_{1 t}^{*}+\beta_{2} x_{2 t}^{*}+u_{t},\quad\beta_{0}^{*}=\beta_{0}(1-\rho) yt∗=β0∗+β1x1t∗+β2x2t∗+ut,β0∗=β0(1−ρ)
以 β 0 ∗ , β 1 , β 2 \beta_{0}^{*}, \beta_{1}, \beta_{2} β0∗,β1,β2 为回归系数的普通回归模型。
DW检验后的处理步骤如下图:
ρ ^ = 1 − D W / 2 = 0.5623 \hat{\rho}=1-DW/2=0.5623 ρ^=1−DW/2=0.5623
作变换:
y i ∗ = y t − 0.5623 y t − 1 y_{i}^{*}=y_{t}-0.5623 y_{t-1} yi∗=yt−0.5623yt−1
x i t ∗ = x i t − 0.5623 x i , t − 1 , i = 1 , 2 x_{i t}^{*}=x_{i t}-0.5623 x_{i, t-1}, \quad i=1,2 xit∗=xit−0.5623xi,t−1,i=1,2
给出程序:
#去掉数据后
yt_1 = [97.4,113.5,125.7,122.8,133.3,149.3,144.2,166.4,195.0,229.8,228.7,206.1,257.9,324.1,386.6,423.0,401.9,474.9,424.5]
x1t_1 = [637.7,691.1,756.0,799.0,873.4,944.0,992.7,1077.6,1185.9,1326.4,1434.2,1594.2,1718.0,1918.3,2163.9,2417.8,2631.7,2954.7,3073.0]
x2t_1 = [0.7277,0.7436,0.7676,0.7906,0.8254,0.8679,0.9145,0.9601,1.0,1.0575,1.1508,1.2579,1.3234,1.4005,1.5042,1.6342,1.7842,1.9514,2.0688]
#广义差分变换
#变换
yt_change = [a - p*b for a,b in zip(yt[1:20],yt_1)]
x1t_change = [c - p*d for c,d in zip(x1t[1:20],x1t_1)]
x2t_change = [e - p*f for e,f in zip(x2t[1:20],x2t_1)]
yt_change = pd.DataFrame(yt_change)
x1t_change = pd.DataFrame(x1t_change)
x2t_change = pd.DataFrame(x2t_change)
touzi['yt_change'] = yt_change
touzi['x1t_change'] = x1t_change
touzi['x2t_change'] = x2t_change
八、新模型求解及验证:
1、求解模型
y t ∗ = β 0 ∗ + β 1 x 1 t ∗ + β 2 x 2 t ∗ + u t y_{t}^{*}=\beta_{0}^{*}+\beta_{1} x_{1 t}^{*}+\beta_{2} x_{2 t}^{*}+u_{t} yt∗=β0∗+β1x1t∗+β2x2t∗+ut.
#新模型
#yt_change = b0_change + b1_1x1t_change + b2_1x2t_change + u
model_2 = sm.formula.ols('yt_change ~ x1t_change + x2t_change', data = touzi).fit() #OLS普通最小二乘法
model_2.summary()
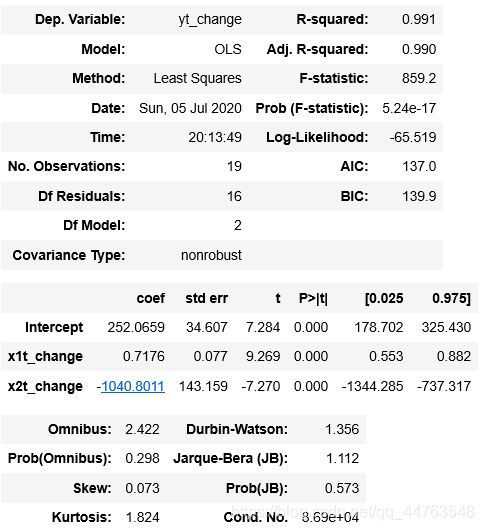
#新模型
equation_yt_change = 'yt_change方程为:' + ' yt_change' + ' = ' + '252.0659' + ' + ' + '0.7176' + '*x1t_change ' + '- ' + '1040.8011' + '*x2t_change'
print(equation_yt_change)
pre_yt_change = 252.0659 + 0.7176*x1t_change - 1040.8011*x2t_change
MSE_change_1 = (yt_change - pre_yt_change)**2/(19)
MSE_change_2 = MSE_change_1.apply(lambda x: x.sum())
MSE_change_3 = cmath.sqrt(MSE_change_2)
print('剩余标准差:\t s_change = ',MSE_change_3,'< s = 12.2853')
print('R2_change = ',0.991)
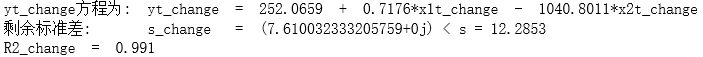
总体效果良好, s n e w = 7.6100 < s o l d = 12.2853 s_{new}=7.6100 \quad <\quad s_{old}=12.2853 snew=7.6100<sold=12.2853
2、新模型的自相关检验
新模型 D W n e w = 1.5751 DW_{new}=1.5751 DWnew=1.5751,样本容量 n = 19 n=19 n=19,回归变量数目 k = 3 k=3 k=3, α = 0.05 \alpha=0.05 α=0.05,通过查表得,临界值 d L = 1.08 , d U = 1.53 d_{L}=1.08,d_{U}=1.53 dL=1.08,dU=1.53.
d U < D W n e w < 4 − d U d_{U}
新模型: y ^ t ∗ = 252.0659 + 0.7176 x 1 t ∗ − 1040.8011 x 2 t ∗ \hat{y}_{t}^{*}=252.0659+0.7176 x_{1 t}^{*}-1040.8011x_{2 t}^{*} y^t∗=252.0659+0.7176x1t∗−1040.8011x2t∗.
还原为原始变量: y ^ t = 252.0659 + 0.5623 y t − 1 + 0.7176 x 1 , t − 1040.8011 x 2 , t − 0.4.35 x 1 , t − 1 + 585.2425 x 2 , t − 1 \hat{y}_{t}=252.0659+0.5623y_{t-1}+0.7176 x_{1,t}-1040.8011x_{2,t}-0.4.35x_{1,t-1}+585.2425x_{2,t-1} y^t=252.0659+0.5623yt−1+0.7176x1,t−1040.8011x2,t−0.4.35x1,t−1+585.2425x2,t−1,称为一阶自回归模型。
其中, 0.4.35 x 1 , t − 1 0.4.35x_{1,t-1} 0.4.35x1,t−1为 0.5623 y t − 1 × ρ 0.5623y_{t-1}\times \rho 0.5623yt−1×ρ; 585.2425 x 2 , t − 1 = 1040.8011 x 2 t × ρ 585.2425x_{2,t-1}=1040.8011x_{2 t} \times \rho 585.2425x2,t−1=1040.8011x2t×ρ.
九、基本回归模型与一阶自回归模型比较:
1、残差图比较
#一阶自回归模型
onelevel_pre_yt =np.array([p*q for q in yt_1]) + np.array([0.7176*r for r in x1t[0:19]]) + np.array([p*(-0.7176)*s for s in x1t_1]) + np.array([-1040.8011*t for t in x2t[0:19]]) + np.array([p*1040.8011*v for v in x2t_1])
#新残差诊断法
et_one = list(yt[0:19]) - onelevel_pre_yt #残差
et_one = list(et_one)
将原模型与新模型(一阶自回归模型)残差归一化,把数据规模转换到[-20,20],进行比较。
#对 et 数据归一化到[-20,20]区间范围
a_min = -20
b_max = 20
et_min = min(et[0:19])
et_max = max(et[0:19])
k=(b_max-a_min)/(et_max - et_min)
et_sta=[(a_min + k*(l - et_min)) for l in et[0:19]]
#对 et_one 数据归一化到[-20,20]区间范围
et_min_one = min(et_one)
et_max_one = max(et_one)
k2=(b_max-a_min)/(et_max_one - et_min_one)
et_sta_one=[(a_min + k2*(ll - et_min_one)) for ll in et_one]
GNP(国民生产总值)的新旧模型残差比较。
#残差与国民生产总值的关系
plt.scatter(x1t[0:19],et_sta,marker = '+')
plt.scatter(x1t[0:19],et_sta_one,marker = '+',color='r')
plt.legend(["原模型","新模型"])

物价指数新旧模型残差比较。
#残差与物价指数的关系
plt.scatter(x2t[0:19],et_sta,marker = '+')
plt.scatter(x2t[0:19],et_sta_one,marker = '+',color='r')
plt.legend(["原模型","新模型"])
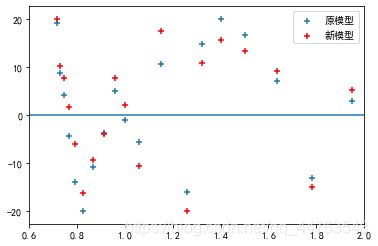
2、拟合图比较
#对 yt 数据归一化到[0,500]区间范围
c_min = 0
d_max = 500
yt_min = min(yt[0:19])
yt_max = max(yt[0:19])
k3=(d_max-c_min)/(yt_max - yt_min)
yt_sta=[(c_min + k3*(lll - yt_min)) for lll in yt[0:19]]
#对 onelevel_pre_yt 数据归一化到[-20,20]区间范围
onelevel_pre_yt_min = min(onelevel_pre_yt)
onelevel_pre_yt_max = max(onelevel_pre_yt)
k4=(d_max-c_min)/(onelevel_pre_yt_max - onelevel_pre_yt_min)
onelevel_pre_yt_sta=[(c_min + k4*(llll - onelevel_pre_yt_min)) for llll in onelevel_pre_yt]
#对 x1t 数据归一化到[0,20]区间范围
e_min = 0
f_max = 20
x1t_min = min(x1t[0:19])
x1t_max = max(x1t[0:19])
k5=(f_max-e_min)/(x1t_max - x1t_min)
x1t_sta=[(e_min + k5*(lllll - x1t_min)) for lllll in x1t[0:19]]
#对 et_one 数据归一化到[-20,20]区间范围
x2t_min = min(x2t[0:19])
x2t_max = max(x2t[0:19])
k6=(f_max-e_min)/(x2t_max - x2t_min)
x2t_sta=[(e_min + k6*(llllll - x2t_min)) for llllll in x2t[0:19]]
#拟合图比较
plt.scatter(x1t_sta[0:19],yt_sta[0:19],marker='o',c='',edgecolors='b')
plt.scatter(x2t_sta[0:19],yt_sta[0:19],marker='+',color='r',edgecolors='b')
plt.legend(["原模型","新模型"])
新旧模型拟合图比较。
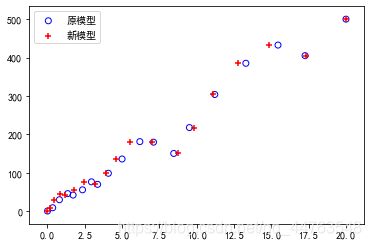
按道理,这里是要看出:一阶自回归模型残差 e e e比基本回归模型要小,这里我也没有明确看出来。
接下来就可以根据方程式进行投资额预测,本文不再展开描述。