最小生成树之普里姆(Prim)算法
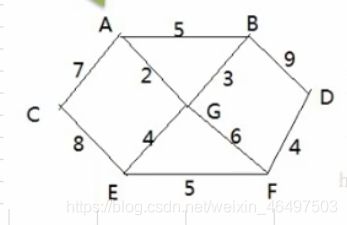
普里姆(Prim)算法(加点法):
(1) 从A顶点开始处理: 得到 < A >
(2) < A >开始,将和 A 顶点相邻并且还没有被访问的顶点进行处理:
A-C[7]; A-G[2]; A-B[5]; 得到
(3)
A-C[7]; A-B[5]; G-B[3]; G-E[4]; G-F[6]; 得到
(4)
(5)
(6)
(7)
一共会生成6条边: A-G[2]; G-B[3]; G-E[4]; E-F[5]; F-D[4]; A-C[7]
(n个顶点的最小二叉树一共有n - 1条边)
代码实现:
public class Prim {
public static void main(String[] args) {
MGraph graph = new MGraph(7);
MinTree minTree = new MinTree();
char[] data = {
'A', 'B', 'C', 'D', 'E', 'F', 'G'};
final int N = 10000;//用10000表示两个结点之间不能连接,或者也可以用Integer.MAX_VALUE
int[][] weight = {
{
N, 5, 7, N, N, N, 2},
{
5, N, N, 9, N, N, 3},
{
7, N, N, N, 8, N, N},
{
N, 9, N, N, N, 4, N},
{
N, N, 8, N, N, 5, 4},
{
N, N, N, 4, 5, N, 6},
{
2, 3, N, N, 4, 6, N}};
minTree.creatGraph(graph, 7, data, weight);
minTree.show(graph);
minTree.prim(graph, 0);
}
}
class MinTree {
public void creatGraph(MGraph graph, int vertex, char[] data, int[][] weight) {
for (int i = 0; i < vertex; i++) {
graph.data[i] = data[i];
for (int j = 0; j < vertex; j++) {
graph.weight[i][j] = weight[i][j];
}
}
}
public void show(MGraph graph) {
for (int i = 0; i < graph.vertex; i++) {
for (int j = 0; j < graph.vertex; j++) {
System.out.print(graph.weight[i][j] + " ");
}
System.out.println();
}
}
/**
* @param graph 将图传进去
* @param v 指从下标为 v 的结点开始
*/
public void prim(MGraph graph, int v) {
boolean[] isVisited = new boolean[graph.vertex];//false表示未被访问过,true表示已经被访问过
//把当前结点标记为已访问
isVisited[v] = true;
//minWeight记录最小权的那个值
int minWeight = 10000;
//h1和h2记录两个顶点的下标
int h1 = -1;
int h2 = -1;
for (int k = 1; k < graph.vertex; k++) {
//因为有n个结点,在算法结束后,一共会有 n - 1 个边
//确定每一次生成的子图,和哪个结点的距离最近(权值最小)
for (int i = 0; i < graph.vertex; i++) {
//i表示已经访问过的结点
for (int j = 0; j < graph.vertex; j++) {
//j表示还未被访问过的结点
//从已经访问过的结点中找到与它们相邻的、还未被访问过的并且权值最小的那个顶点,其下标即 h2
if (isVisited[i] == true && isVisited[j] == false && graph.weight[i][j] < minWeight) {
//如果i结点被访问过并且j结点未被访问并且当前权值小于最小权值
minWeight = graph.weight[i][j];
h1 = i;
h2 = j;
}
}
}
//将这个结点标记为已经访问
isVisited[h2] = true;
System.out.println("边<" + graph.data[h1] + ", " + graph.data[h2] + ">, 其权值为:" + graph.weight[h1][h2]);
//minWeight 重新赋值为最大值10000
minWeight = 10000;
}
}
}
class MGraph {
int vertex;//记录结点的个数
char[] data;//记录各个结点的值
int[][] weight;//记录邻接矩阵
public MGraph(int n) {
vertex = n;
data = new char[n];
weight = new int[n][n];
}
}