Codeforces Round #696 (Div. 2)(A~D题解)
Codeforces Round #696 (Div. 2)(A~C题解)
——南昌理工学院ACM集训队
题目链接:https://codeforces.ml/contest/1474
A. Puzzle From the Future
In the 2022 year, Mike found two binary integers a and b of length n (both of them are written only by digits 0 and 1) that can have leading zeroes. In order not to forget them, he wanted to construct integer d in the following way:
he creates an integer c as a result of bitwise summing of a and b without transferring carry, so c may have one or more 2-s. For example, the result of bitwise summing of 0110 and 1101 is 1211 or the sum of 011000 and 011000 is 022000;
after that Mike replaces equal consecutive digits in c by one digit, thus getting d. In the cases above after this operation, 1211 becomes 121 and 022000 becomes 020 (so, d won’t have equal consecutive digits).
Unfortunately, Mike lost integer a before he could calculate d himself. Now, to cheer him up, you want to find any binary integer a of length n such that d will be maximum possible as integer.
Maximum possible as integer means that 102>21, 012<101, 021=21 and so on.
Input
The first line contains a single integer t (1≤t≤1000) — the number of test cases.
The first line of each test case contains the integer n (1≤n≤105) — the length of a and b.
The second line of each test case contains binary integer b of length n. The integer b consists only of digits 0 and 1.
It is guaranteed that the total sum of n over all t test cases doesn’t exceed 105.
Output
For each test case output one binary integer a of length n. Note, that a or b may have leading zeroes but must have the same length n.

题意:
现有两个长度为n的0,1字符串a,b(其中仅包含0,1),对两个字符串相加得到字符串c(按数值不进位相加);
例如:
a=“011011”;
b=“101101”;
则c=“112112”;
之后将c中的连续重复数字替换为一位得到字符串d,对于上述c它的对应字符串d=“1212”;
输出:题目给出一个字符串b;求一个字符串a使得a+b对应的字符串d最大;
解析:
根据题意可以看出本题利用已知的字符串b来构造字符串a;
由题意已知,字符串d的构造方法,需要去掉c中连续重复的字符,则在构造的过程中应使得c[i]与c[i-1]不相同(字符串长度最大),同时要使c尽可能大;
因为a与b都是01串,如果b[i]==0,则c[i]==0||c[i]==1,此时a[i]+b[i]最大为1,看c[i-1]是否为1,如果c[i-1]==1那么a[i]不能取1(取1则c[i]==1,会缩短字符串长度)否则取a[i]=1;
若b[i]==1,则c[i]==1||c[i]==2,同理看c[i-1]是否为2;
#include因为每一位只与前一位有关系,所以可以边构造边输出;
B. Different Divisors
Positive integer x is called divisor of positive integer y, if y is divisible by x without remainder. For example, 1 is a divisor of 7 and 3 is not divisor of 8.
We gave you an integer d and asked you to find the smallest positive integer a, such that
a has at least 4 divisors;
difference between any two divisors of a is at least d.
Input
The first line contains a single integer t (1≤t≤3000) — the number of test cases.
The first line of each test case contains a single integer d (1≤d≤10000).
Output
For each test case print one integer a — the answer for this test case.
input
2
1
2
output
6
15
题意:
题意比较简单
给了一个整数d让我们找出最小的正整数a,使得a至少有4个因子且a的任意两个因数之差至少为d。
解析:
1:对于一些素数p和q,整数有4个约数,如果它的形式是p×q或p3。在第一种情况下,它有1,p, q, pq。
在第二种情况下,它有因子1 p p2 p3。
2:根据贪心,本题不是找到至少有4个约数的整数,而是找到恰好有4个约数的整数(任意两个因数相差大于等于d)。
3:若p为a最小的质因数,要使得任意两个因数只差至少为d则p≥d+1。
则解法为:
四个因数,第一个为1,第四个为a,则中间两个就为第一个比1大于等于d的质数和第一个比第二个因数大于等于的质数,将它们相乘即可得到 a
即:1,d+m,d+m+n,(d+m)(d+d+m)(m为找不到恰好相差d的时候找到的第一个大于d的质数-d,n同理)
#include
// }
while(T--){
scanf("%d",&n);//差值n
ll ans=0;
ll a=upper_bound(primer,primer+cnt,n)-primer;//二分查找找到第一个差值为n的质数;
a=primer[a];
ll b=lower_bound(primer,primer+cnt,a+n)-primer;//二分查找找到第二个差值为n的质数
b=primer[b];
ans=a*b;//相乘求得ans的值
cout<<ans<<endl;
}
return 0;
}
C. Array Destruction
You found a useless array a of 2n positive integers. You have realized that you actually don’t need this array, so you decided to throw out all elements of a.
It could have been an easy task, but it turned out that you should follow some rules:
In the beginning, you select any positive integer x.
Then you do the following operation n times:
select two elements of array with sum equals x;
remove them from a and replace x with maximum of that two numbers.
For example, if initially a=[3,5,1,2], you can select x=6. Then you can select the second and the third elements of a with sum 5+1=6 and throw them out. After this operation, x equals 5 and there are two elements in array: 3 and 2. You can throw them out on the next operation.
Note, that you choose x before the start and can’t change it as you want between the operations.
Determine how should you behave to throw out all elements of a.
Input
The first line contains a single integer t (1≤t≤1000) — the number of test cases.
The first line of each test case contains the single integer n (1≤n≤1000).
The second line of each test case contains 2n integers a1,a2,…,a2n (1≤ai≤106) — the initial array a.
It is guaranteed that the total sum of n over all test cases doesn’t exceed 1000.
Output
For each test case in the first line print YES if it is possible to throw out all elements of the array and NO otherwise.
If it is possible to throw out all elements, print the initial value of x you’ve chosen. Print description of n operations next. For each operation, print the pair of integers you remove.
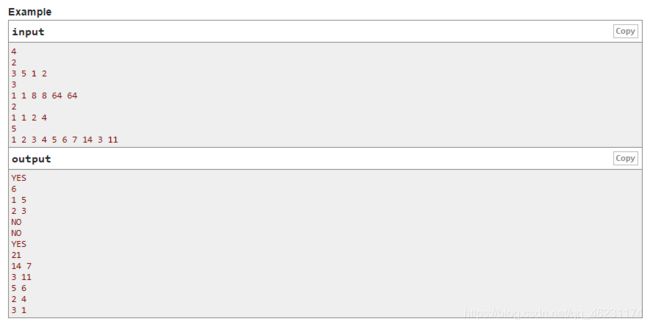
题意:
给出一个长度为2*n的数组;
一开始,你选择任意正整数x。
然后做下面的操作n次:
选择数组中的两个元素u,v,使得u+v = x;
然后从a中移除u与v,并用这两个数的最大值替换x。
对于每个测试用例,如果可以抛出数组中的所有元素,则打印YES,否则打印NO。
如果可以抛出所有元素,则打印所选择的x的初始值。接下来打印n个操作的描述。对于每个操作,打印要删除的一对整数u,v。
例如,如果初始a=[3,5,1,2],则可以选择x=6。然后你可以用sum 5+1=6选择a的第二个和第三个元素并把它们扔出去。在这个操作之后,x等于5,数组中有两个元素:3和2。下次手术的时候你就可以扔了。
解析:
由题意可知,更新的x为抛弃的u,v的最大值(且u+v==x才能抛弃,a[i]不为负数),则无论第一个x取值为多少,第一轮抛弃中必定有a中最大的数字max(a),否则在之后的抛弃中max(a)永远无法抛弃,同理第二轮抛弃中必定有a中第二大的数字,第三轮抛弃中必定有a中第三大的数字……
我开始的想法是,先将数组排序,for循环从后往前遍历,先以最大值为x查找每一轮的u,v,之后用vis数组标记,之后剩余的那个数字与最大值匹配得到初始的x0,但是这个想法样例都过不了;
最后一个样例:
5
1 2 3 4 5 6 7 14 3 11
排序后
1 2 3 3 4 5 6 7 11 14
对这个数组进行上述操作:
x=14->u1=11,v1=3->x=11
x=11->u2=7,v2=4->x=7(这里就开始不对劲了QAQ)
x=7->u3=6,v3=1->x=6
x=6->无法匹配,NO
很显然这个贪心是错误的;还是得先求出初始的x0
仔细读题发现“It is guaranteed that the total sum of n over all test cases doesn’t exceed 1000.”(确保所有测试用例中n的总和不超过1000。)哦阔ヾ(≧▽≦)o*
直接先把初始的x0求出来,那么如何找到初始的x0?枚举!
枚举每一个数与最大的数相匹配,将这两个数抛弃,之后的操作就和上面的贪心一样
#include
// cout<
int flag=0;
int cnt=0;
for(int k=1;k<n;k++){
memset(v,0,sizeof(v));//清空
int x=a[n];
cnt=0;
f[++cnt].x=a[k];f[cnt].y=x;//存u,v
v[n]=1;v[k]=1;//标记
flag=0;
for(int i=n-1;i>=1;i--){
if(v[i]==0){
v[i]=1;
int ans=find(x-a[i]);//查找相匹配的值,返回-1为没有找到
if(ans!=-1){
f[++cnt].x=a[ans];
f[cnt].y=a[i];
x=max(a[i],a[ans]);
v[i]=1;v[ans]=1;
}
else{
//没找到直接下一轮查找
flag=1;break;
}
}
}
if(flag==0){
//全部找到了,就跳出
break;
}
}
if(flag==1){
printf("NO\n");
continue;
}
printf("YES\n");
printf("%d\n",f[1].x+f[1].y);
for(int i=1;i<=cnt;i++){
printf("%d %d\n",f[i].x,f[i].y);
}
}
return 0;
}
小蔡姬实力有限,只会这三题,见谅(‾◡◝)
科普一下这个lower_bound( )
lower_bound( )和upper_bound( )都是利用二分查找的方法,左闭右开的有序区间里进行二分查找的。
两个函数在algorithm头文件下;
lower_bound( begin,end,num):从数组的begin位置到end-1位置二分查找第一个大于或等于num的数字;
upper_bound( begin,end,num):从数组的begin位置到end-1位置二分查找第一个大于num的数字;
找到返回该数字的地址,不存在则返回end。
来补个D题,刚刚看完大佬的博客
大佬的博客(原文)
D. Cleaning
During cleaning the coast, Alice found n piles of stones. The i-th pile has ai stones.
Piles i and i+1 are neighbouring for all 1≤i≤n−1. If pile i becomes empty, piles i−1 and i+1 doesn’t become neighbouring.
Alice is too lazy to remove these stones, so she asked you to take this duty. She allowed you to do only the following operation:
Select two neighboring piles and, if both of them are not empty, remove one stone from each of them.
Alice understands that sometimes it’s impossible to remove all stones with the given operation, so she allowed you to use the following superability:
Before the start of cleaning, you can select two neighboring piles and swap them.
Determine, if it is possible to remove all stones using the superability not more than once.
Input
The first line contains a single integer t (1≤t≤104) — the number of test cases.
The first line of each test case contains the single integer n (2≤n≤2⋅105) — the number of piles.
The second line of each test case contains n integers a1,a2,…,an (1≤ai≤109) — the number of stones in each pile.
It is guaranteed that the total sum of n over all test cases doesn’t exceed 2⋅105.
Output
For each test case, print YES or NO — is it possible to remove all stones using the superability not more than once or not.

题意:
给出n堆石头,第i堆有ai个石头,现在需要清空这些石头,可执行的操作为:
1、选择两个相邻的堆,如果它们都不是空的,从每个堆中移出一块石头。
2、在开始清理前,可以选择相邻的两堆并进行交换。(仅限一次)
现在请问能否将这n堆石头清空
对于所有1≤i≤n−1的堆i和i+1是相邻的。如果第i堆变成空的,第i - 1堆和第i+1堆就不会相邻。
能清空输出YES,否则输出NO
解析:
题目给了两种操作,我们首先考虑一个子问题没有操作2的时候怎样判断是否能清空数组;
首先发现一点,左右端点的石子能否清零仅由它们后面的那一堆石子的数量决定,即端点值数应小于等于它们后面的值,否则必定为NO
a2>=a1时,便可清空a1,此时a2=a2-a1,a2变为端点值,如此便可以从左往右不断更新端点值;
同理也可从左往右不断更新右边的端点值
用一个前缀数组和一个后缀数组分别去记录中间的过程;
注:若是中途出现pre[i-1]>a[i]的,那么此时意味着如果将这两个相邻的减了,就将导致a[i-1]变成空,不能满足题目的要求,对于这种情况,先定义两个不同的较大值(比a[i]范围大),记录pre[i]为其中一个较大值;同理suf遇到这种情况则赋值为另一个较大值(在交换相邻项的时候需要判前后缀是否相等,两个较大值不能相同)
求出两个数组:pre[i]=a[i]-pre[i-1] ;suf[i]=a[i]-suf[i+1] ;
假如说有解的话,那么一定有一个分界点i使得他俩合并起来之后有什么相等条件表示,使得左右两边都可以删除完,很显然这个条件为pre[i]==suf[i+1]
简单的讲pre[i]表示从左往右消剩余的石子,suf[i+1]表示从右往左消剩余的石子
当pre[i]==suf[i+1]的时候就相当于只剩两堆石子,且两堆石子数量相等(这不就一下就消掉了吗)
上述方法是不考虑操作2的情况,那么当我们考虑操作2
即为当**pre[i]!=suf[i+1]**我们可以将a[i]与a[i+1]的值交换再进行一次判断;
总结:先构造出上述的前后缀数组pre和suf,之后从一个循环左往右枚举pre[i]的值和suf[i+1]的值是否相等,相等即为YES跳出循环;若是不相等,则交换a[i]与a[i+1]①(下解释交换)然后判断,若是相等则为YES后跳出,否则进入下一重循环。
①如何交换a[i]与a[i+1]:当不匹配的时候交换然后重新求pre和suf数组?当然不可能,限时2 seconds都不允许你这么操作,此时:
已知:pre[i]=a[i]-pre[i-1];
suf[i+1]=a[i+1]-suf[i+2];
那么交换a后的pre[i]和suf[i+1]是不是就一目了然
交换后pre[i]=a[i+1]-suf[i+2] ; suf[i+1]=a[i+1]-pre[i-1] ;(注意这里要判断一下是否为负数)
#include扯完了,掰掰!