Pointfilter: Point Cloud Filtering via Encoder-Decoder Modeling论文解读
Pointfilter: Point Cloud Filtering via Encoder-Decoder Modeling 论文解读
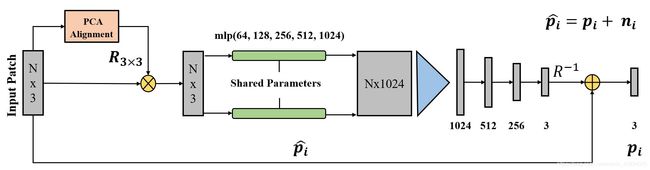
1. METHOD
学习的是位移矢量,噪点+位移矢量=去噪后的点
1.1 Preprocessing
给定一组点云 P P P和 P ^ \hat{P} P^,定义噪声块 P ^ \hat{\mathcal{P}} P^和其对应的真实块 P \mathcal{P} P
P i ^ = { p j ^ ∣ ∥ p j ^ − p i ^ ∥ < r } P i = { p j ∣ ∥ p j − p i ∥ < r } \hat{\mathcal{P_i}} = \{\hat{p_j} \mid \Vert\hat{p_j}-\hat{p_i}\Vert < r\}\\ \mathcal{P_i}= \{p_j \mid \Vert\ p_j-p_i \Vert < r\} Pi^={ pj^∣∥pj^−pi^∥<r}Pi={ pj∣∥ pj−pi∥<r}
r r r是块的半径,一般为模型包围盒对角线的5%。
一旦生成了块,在点云滤波中就要考虑两个问题:
- 如何避免观察域中不必要的自由度;
- 如何保证Pointfilter对某些几何变换敏感。
对于问题1,可以将块变换到原点(以 p i ^ \hat{p_i} pi^为中心),并且进行以下伸缩变换
P i ^ = ( P i ^ − p i ^ ) / r P i = ( P i − p i ^ ) / r \hat{\mathcal{P_i}}=(\hat{\mathcal{P_i}}-\hat{p_i}) \verb|/|r\\ \mathcal{P_i}=(\mathcal{P_i}-\hat{p_i}) \verb|/|r Pi^=(Pi^−pi^)/rPi=(Pi−pi^)/r
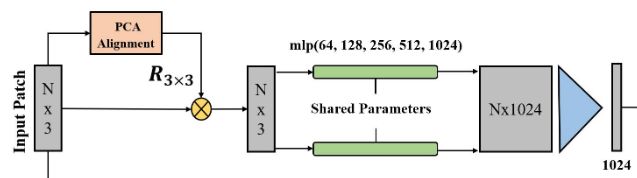
为了保证刚体不变性,将输入块的PCA主轴与笛卡尔空间进行对齐(先对齐z轴,再对齐x轴)。
为了方便调参,设置输入块的点的默认数量为 ∣ P i ^ ∣ = 500 \mid\hat{\mathcal{P_i}}\mid=500 ∣Pi^∣=500。当块点的数量小于500,填充;当点数大于500,进行随机下采样。
1.2 The Pointfilter Framework
主要想法:根据其相邻结构将每个噪声点投影到基础表面上。
The key idea of our Pointfilter is to project each noisy point onto the underlying surface according to its neighboring structure.
为了实现上诉想法,作者设计了有个编码-解码网络。
1.2.1 Encoder
输入:经过PCA处理的点云块。
目的:从输入块中获得复杂的表示信息。
编码器包含两个部分:
- 特征提取器(MLPs),提取不同尺度的特征。
- 收集器(collector),将特征( N × 1024 N\times1024 N×1024)转化为一个1024维向量。(max pooling)
对于图中的shared Parameters,其实并没有什么特别的地方,其实就是MLPs。PointNet上也是这么写的。代码和PointNet差不多,不过增加了Batch Normalization,以保证每一层特征都是标准分布。
代码如下:
class pointfilter_decoder(nn.Module):
def __init__(self):
super(pointfilter_decoder, self).__init__()
self.fc1 = nn.Linear(1024, 512)
self.fc2 = nn.Linear(512, 256)
self.fc3 = nn.Linear(256, 3)
self.bn1 = nn.BatchNorm1d(512)
self.bn2 = nn.BatchNorm1d(256)
self.dropout_1 = nn.Dropout(0.3)
self.dropout_2 = nn.Dropout(0.3)
def forward(self, x):
x = F.relu(self.bn1(self.fc1(x)))
# x = self.dropout_1(x)
x = F.relu(self.bn2(self.fc2(x)))
# x = self.dropout_2(x)
x = torch.tanh(self.fc3(x))
return x
1.2.2 Decoder
解码器就比较暴力,直接FCN。但在最后要将点转回原来的坐标域,所以要乘 R − 1 R^{-1} R−1。
至于最后为什么有个 + + +,通过后面公式
p i ˉ = r R − 1 f ( R ( P i ^ − p i ^ / r ) ) + p i ^ \bar{p_i}=rR^{-1}f(R(\hat{\mathcal{P_i}}-\hat{p_i}/r))+\hat{p_i} piˉ=rR−1f(R(Pi^−pi^/r))+pi^
可知,所学习的内容其实是去噪去掉的部分,对于点来说,其实 r R − 1 f ( R ( P i ^ − p i ^ / r ) ) rR^{-1}f(R(\hat{\mathcal{P_i}}-\hat{p_i}/r)) rR−1f(R(Pi^−pi^/r))就是一个位移矢量。
代码如下:
class pointfilter_decoder(nn.Module):
def __init__(self):
super(pointfilter_decoder, self).__init__()
self.fc1 = nn.Linear(1024, 512)
self.fc2 = nn.Linear(512, 256)
self.fc3 = nn.Linear(256, 3)
self.bn1 = nn.BatchNorm1d(512)
self.bn2 = nn.BatchNorm1d(256)
self.dropout_1 = nn.Dropout(0.3)
self.dropout_2 = nn.Dropout(0.3)
def forward(self, x):
x = F.relu(self.bn1(self.fc1(x)))
# x = self.dropout_1(x)
x = F.relu(self.bn2(self.fc2(x)))
# x = self.dropout_2(x)
x = torch.tanh(self.fc3(x))
return x
1.2.3 Loss function
为了尽可能的保证去噪后的点云接近于真实点云,并且能够保留尖锐的特征,作者定义了两种loss。
L p r o j a = ∑ p j ∈ P i ∣ ( p i ˉ − p j ) ⋅ n p j T ∣ ⋅ ϕ ( ∥ p i ˉ − p j ∥ ) ∑ p j ∈ P i ϕ ( ∥ p i ˉ − p j ∥ ) L^a_{proj} = \frac{\sum_{p_j\in \mathcal{P_i}}\mid (\bar{p_i}-p_j)\cdot n^T_{p_j}\mid \cdot \phi(\Vert\bar{p_i}-p_j\Vert)}{\sum_{p_j\in \mathcal{P_i}}\phi(\Vert\bar{p_i}-p_j\Vert)} Lproja=∑pj∈Piϕ(∥piˉ−pj∥)∑pj∈Pi∣(piˉ−pj)⋅npjT∣⋅ϕ(∥piˉ−pj∥)
其中, n p j n_{pj} npj是真实点云中 p j p_j pj的法向, ϕ ( ∥ p i ˉ − p j ∥ ) \phi(\Vert\bar{p_i}-p_j\Vert) ϕ(∥piˉ−pj∥)是高斯函数
ϕ ( ∥ p i ˉ − p j ∥ ) = e x p ( ∥ p i ˉ − p j ∥ 2 σ p 2 ) \phi(\Vert\bar{p_i}-p_j\Vert)=exp(\frac{\Vert\bar{p_i}-p_j\Vert^2}{\sigma_p^2}) ϕ(∥piˉ−pj∥)=exp(σp2∥piˉ−pj∥2)
其中, σ p \sigma_p σp定义为 σ p = d i a g / m \sigma_p=\sqrt{diag/m} σp=diag/m, d i a g diag diag的大小为 P i \mathcal{P_i} Pi的包围盒的对角线长度, m = ∣ P i ^ ∣ m=\mid\hat{\mathcal{P_i}}\mid m=∣Pi^∣。
除了保证去噪后的点云接近真实点云,还希望去噪后的点分布均匀。为了达成这一目标,用排斥项来惩罚点的聚合。
L = η L p r o j a + ( 1 − η ) L r e p , L r e p = m a x p j ∈ P i ∣ p i ˉ − p j ∣ L=\eta L^a_{proj}+(1-\eta)L_{rep},L_{rep}=max_{p_j \in \mathcal{P_i}\mid }\bar{p_i}-p_j\mid L=ηLproja+(1−η)Lrep,Lrep=maxpj∈Pi∣piˉ−pj∣
其中, η \eta η为权衡参数,作者设 η = 0.97 \eta=0.97 η=0.97进行训练。
上面这个loss的定义有点像高斯滤波。事实上,在实验的过程中,使用这一loss,确实会使尖锐的特征变得平滑。基于双边滤波在保留特征上的优势,作者增加了当前点与领域点的法向相似性作为约束,得到了如下loss:
L p r o j b = ∑ p j ∈ P i ∣ ( p i ˉ − p j ) ⋅ n p j T ∣ ⋅ ϕ ( ∥ p i ˉ − p j ∥ ) θ ( n p i ˉ , n p j ) ∑ p j ∈ P i ϕ ( ∥ p i ˉ − p j ∥ ) θ ( n p i ˉ , n p j ) L^b_{proj} = \frac{\sum_{p_j\in \mathcal{P_i}}\mid (\bar{p_i}-p_j)\cdot n^T_{p_j}\mid \cdot \phi(\Vert\bar{p_i}-p_j\Vert)\theta(n_{\bar{p_i}},n_{p_j})}{\sum_{p_j\in \mathcal{P_i}}\phi(\Vert\bar{p_i}-p_j\Vert)\theta(n_{\bar{p_i}},n_{p_j})} Lprojb=∑pj∈Piϕ(∥piˉ−pj∥)θ(npiˉ,npj)∑pj∈Pi∣(piˉ−pj)⋅npjT∣⋅ϕ(∥piˉ−pj∥)θ(npiˉ,npj)
其中
θ ( n p i ˉ , n p j ) = e x p ( − 1 − n p i ˉ T n p j 1 − c o s ( σ n ) ) \theta(n_{\bar{p_i}},n_{p_j})=exp(-\frac{1-n^T_{\bar{p_i}}n_{p_j}}{1-cos(\sigma_n)}) θ(npiˉ,npj)=exp(−1−cos(σn)1−npiˉTnpj)
σ n \sigma_n σn是支持角,默认设为15°,噪声块中每个点的法向 n p i ˉ n_{\bar{p_i}} npiˉ定义为离其最近的真实块中的点的法向。
2 优缺点
2.1 优点
- 可以学习复杂和紧凑的点云的表示形式。
- 结合了一些传统的去噪方法进行loss设计。
2.2 缺点
在噪声很多的情况下,对尖锐的噪声保留效果不是很好。