阅读心得:TGCN:Time Domain Graph Convolutional Network For Multiple Objects Tracking
论文地址:TGCN:Time Domain Graph Convolutional Network For Multiple Objects Tracking
TGCN
- 一、 摘要
- 二、 介绍与相关工作
- 三、 模型
-
- 1、 基于CNN的目标检测方法
- 2、 运动状态估计
- 3. 基于姿态特征提取的TGCN
- 4. 关联
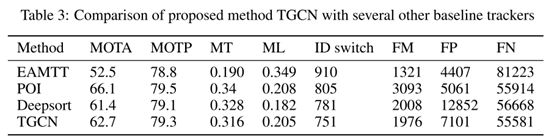
- 四、 实验结果
一、 摘要
作者认为当前MOT的大多数任务在匹配特征时,都没有过多的关注过去帧和当前帧特征之间的时域关联。于是作者使用了一个时域的图卷积来进行任务建模,主要分为两部分。首先使用CNN去提取路人的外貌特征,然后使用GCN对过去帧外貌特征建模,来进行当前帧的特征预测。此操作可以根据过去一些帧之间的关系得到当前帧的姿态特征,从而达到在MOT16上MOTA相较于DeepSORT提升了1.3个点。
二、 介绍与相关工作
在MOT行人追踪任务,大部分动作例如行走在时域上是持续的且有周期的,于是尝试GCN来进行建模姿态特征。如下图,在 t t t帧和 t − 1 t-1 t−1帧中增加关联作为先验知识,对于 t − i t-i t−i帧和 t t t帧之间使用一个数据驱动的概率模型建立关系。几层GCN后就可以通过过去帧的关系来获得当前帧的特征。

作者认为那些直接使用上一帧的运动特征等作为关联依据可能是存在问题的,因为当前帧的姿态特征不一定和上一帧关联,也可能是和之前的 t − i t-i t−i帧关联(运动的周期性)。
作者受图网络启发,提出了一个使用时域图来建模不同帧之间关系信息,并使用一个新颖的时域图神经网络(TGCN)来完成MOT。
三、 模型
TGCN主要包括四个部分:
- 基于CNN的检测,
- 运动状态评估,
- 基于姿态特征提取的TGCN,
- 基于卡尔曼滤波和姿态距离的关联。
1、 基于CNN的目标检测方法
检测器使用端到端的YOLOv5实时检测框架,和使用Faster RCNN检测进行对比,证明检测器对于追踪效果影响不小:

2、 运动状态估计
基于deepsort的方法,加入了速度向量。使用卡尔曼滤波预测六个参数 ( x , y , w , h , v x , v y ) (x, y, w, h, vx, vy) (x,y,w,h,vx,vy)。 x , y , w , h x, y, w, h x,y,w,h为边界框信息,vx, vy是速度信息。增加速度向量主要为了减少基于外貌特征的误匹(例如两个人穿着相似面对面走过时,就容易发生IDSW)。
首先使用第一帧检测结果来初始化卡尔曼滤波,然后用他预测下一帧的位置和速度,最后使用下一帧的检测来纠正卡尔曼滤波,重复二三步。

3. 基于姿态特征提取的TGCN
姿态特征通过CNN提取的行人外貌特征和GCN描述的过去i帧的时空关系特征之和得到。此次实验,使用ResNet-101作为外貌特征提取网络。将训练图片resize到 448 × 448 448 × 448 448×448分辨率,经过多个卷积层后由最大池化获得特征图M( M ∈ R 2048 × 1 M \in R^{2048×1} M∈R2048×1)。定义时间窗口C,输入到GCN网络的是 X 0 X^0 X0, X 0 ∈ R C × 2048 X^0\in R^{C × 2048} X0∈RC×2048。使用一个L层的GCN模型进行时空关系表示和学习。层级传播公式:
X ( l + 1 ) = σ ( A X ( l ) W ) (1) X^{(l+1)}=\sigma\left(A X^{(l)} W\right) \tag{1} X(l+1)=σ(AX(l)W)(1)
A ∈ R C ∗ C A∈R^{C*C} A∈RC∗C是关联矩阵, l l l层表示特征 X ( l ) ∈ R C ∗ d , l = 0 , 1 , … , L − 1 X^{(l)}∈R^{C*d},l={0,1,…,L-1} X(l)∈RC∗d,l=0,1,…,L−1。 σ ( . ) σ(.) σ(.)是激活函数, W W W是层级可训练参数。GCN后获得输出 X ( L ) ∈ R 1 × C X^{(L)}\in R^{1×C} X(L)∈R1×C。
根据先验知识,得到 t − 1 t-1 t−1帧和 t t t帧应该相连接,所以定义矩阵 Q Q Q:
Q = [ 0 1 0 ⋯ 0 0 0 1 ⋯ 0 ⋮ ⋮ ⋮ ⋱ ⋮ 0 0 0 ⋯ 0 ] (2) Q=\left[\begin{array}{ccccc} 0 & 1 & 0 & \cdots & 0 \\ 0 & 0 & 1 & \cdots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & \cdots & 0 \end{array}\right]\tag{2} Q=⎣⎢⎢⎢⎡00⋮010⋮001⋮0⋯⋯⋱⋯00⋮0⎦⎥⎥⎥⎤(2)
定义矩阵P:
P = [ p 0 , 0 p 0 , 1 p 0 , 2 ⋯ p 0 , t p 1 , 0 p 1 , 1 p 1 , 2 ⋯ p 1 , t ⋮ ⋮ ⋮ ⋱ ⋮ p t , 0 p t , 1 p t , 2 ⋯ p t , t ] (3) P=\left[\begin{array}{ccccc} p_{0,0} & p_{0,1} & p_{0,2} & \cdots & p_{0, t} \\ p_{1,0} & p_{1,1} & p_{1,2} & \cdots & p_{1, t} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ p_{t, 0} & p_{t, 1} & p_{t, 2} & \cdots & p_{t, t} \end{array}\right] \tag{3} P=⎣⎢⎢⎢⎡p0,0p1,0⋮pt,0p0,1p1,1⋮pt,1p0,2p1,2⋮pt,2⋯⋯⋱⋯p0,tp1,t⋮pt,t⎦⎥⎥⎥⎤(3)
p i , j p_{i,j} pi,j代表 j j j帧特征最近 i i i帧的概率。最终得到邻接矩阵 A A A:
A = Q + P (4) A = Q+P \tag 4 A=Q+P(4)
损失函数 L L L:
L = ( M t + 1 − X t ( 0 ) ∗ X t ( L ) ) 2 (5) L=\left(M_{t+1}-X_{t}^{(0)} * X_{t}^{(L)}\right)^{2} \tag{5} L=(Mt+1−Xt(0)∗Xt(L))2(5)
4. 关联
使用传统的匈牙利算法进行关联,对于运动信息,用传统的马氏距离计算边界框 ( x , y , w , h ) (x, y, w, h) (x,y,w,h)之间的距离 d 1 d_1 d1,对于速度分量的距离,单独定义距离 d 2 d_2 d2:
d 2 = 1 − cos ( θ ) = 1 − v 1 v 2 ∥ v 1 ∥ ∥ v 2 ∥ (6) d_{2}=1-\cos (\theta)=1-\frac{v_{1} v_{2}}{\left\|v_{1}\right\|\left\|v_{2}\right\|} \tag{6} d2=1−cos(θ)=1−∥v1∥∥v2∥v1v2(6)
定义 d 3 d_3 d3用于测量姿态特征的相似度,定义匈牙利算法的相似度 D D D:
D = λ 1 ( d 1 ) + λ 2 ( d 2 ) + ( 1 − λ 1 − λ 2 ) ( d 3 ) (7) D=\lambda_{1}\left(d_{1}\right)+\lambda_{2}\left(d_{2}\right)+\left(1-\lambda_{1}-\lambda_{2}\right)\left(d_{3}\right) \tag{7} D=λ1(d1)+λ2(d2)+(1−λ1−λ2)(d3)(7)