深度学习基础——以图像风格迁移项目为导向
深度学习基础(讯飞)
- 内容
- 项目
- 1.人工智能概述
-
- 1.1 什么是人工智能?
-
- 发展
- 定义
- 1.2 人工智能的市场应用
- 1.3 人工智能的价值
-
- 商业模式
- 取代人力
- 计算革命
- 2.深度学习路线
-
- 2.1编程与数学
- 2.2深度学习路线
- 3.变量
-
- 3.1字符串
-
- 字符串大小写处理
- 字符串格式化
- 3.2数字
-
- 数字类型
- 数字格式化
- 3.3布尔型
- 4.容器
-
- 4.1列表(lists)
-
- 创建列表
- 列表元素操作
- 列表增删查改
- 切片(前闭后开)
- 4.2元组(dictionaries)
-
- 创建元组(和列表几乎一样)
- 无法修改元素
- 4.3字典(tuples)
-
- 创建和添加
- 删除
- 4.4三个容器对比
- 5.流程控制
- 6.函数和类
- 7.数值计算扩展库Numpy
-
- 7.1数组的创建
-
- array()
- arange()
- zeros() ones()
- 7.2数组的形状
-
- shape
- reshape
- 7.3存取元素
- 7.4加减乘除开方
- 8.二维绘图库Matplotlib
- 9.pytorch简介
-
-
- Pytorch的优势:
-
- 10.pytorch的数据预处理工具:torchvision
-
- 简介
- 组成
- transforms
- 11. 从生物神经网络到感知机
-
- 11.1生物神经网络
- 11.2感知机
-
- 简化描述
- 12.从神经网络到深度学习
-
- 12.1神经网络
-
- 浅层神经网络
- 深层神经网络
- 12.2深度学习
-
- 为什么深度学习会风靡?
- 13.神经网路工作原理
- 14.损失函数
- 15.优化算法
-
- 15.1pytorch优化器
- 15.2梯度下降原理
-
- 导数知识
- 梯度下降基本思想:下山的过程
- 数学解释
- 15.3常用优化器分析
-
- SGD:随机梯度下降
- Adagrad:自动变更学习速率
- RMSprop:对Adagrad的一种改进
- Adam:默认的优化算法
- 16.反向传播算法
-
- 16.1计算图
- 16.2反向传播
- 16.3atuograd-自动求导
- 17.激活函数
-
-
- 常见的激活函数
-
- 18.卷积神经网络基础
-
-
- 卷积层
-
- 卷积通用公式
- 池化层
-
- 池化通用公式
- 全连接层
-
- 19.卷积神经网络模型
-
- LeNet
- VGGNet
- 20.图像风格迁移原理
-
-
- Fast Neural Style.
- VGG-16
-
- 21.图像风格迁移实战
-
- 损失函数计算
- 训练过程
内容
- 编程基础
- 神经网络工作原理
- pytorch深度学习模型的搭建
项目
- 了解人工智能
- 熟悉深度学习模型构建
- 图像风格迁移项目
1.人工智能概述
1.1 什么是人工智能?
发展
- 基于逻辑规则的人工智能(符号主义)
- 基于统计学的机器学习时代(连接主义)
- 深度学习时代
合理的思考->像人一样思考->像人一样行动->合理的行动
定义
- 机器通过学习而掌握合理解决问题的技能。
- 通过对大量数据的学习,具有举一反三的能力。
1.2 人工智能的市场应用
- 医疗:智能牙科病变排查、肝病影像智能诊断
- 商业:人脸识别、千人千面推荐算法、汽车调度系统
- 工业:工业流水线智能排查、3C面板人工智能缺陷检测、人工智能安全监控、无人机轨道群控、工业机器人
1.3 人工智能的价值
商业模式
- 供应链管理
- 精准营销
- 组织架构
- 产品生产
取代人力
- 重复性
- 日常性
- 优化性
- 复杂性
- 创意性
计算革命
- 5G+AI
2.深度学习路线
2.1编程与数学
- TensorFlow
- pytorch
- scikit-learn
2.2深度学习路线
- 基础篇
python
- numpy
- matplotlib
- notebook
- 线性回归
- logistic回归
- 入门篇
TensorFlow or pytorch
感知机->
多层神经网络->
CNN(卷积神经网络)、RNN(递归神经网络)->
AE(自动编码器)、GAN(生成式对抗网络)、DRL(深度强化学习)
- 应用篇
开源数据集
- 语音
- 自然语言处理
- 计算机视觉
- 机器人
3.变量
编程的本质:数据流的控制
Q:如何进行数据的表达和装载?
A:变量
3.1字符串
字符串大小写处理
str='hello,lvshuai'
str.title() # Hello,Lvshuai(每一个单词的首字母都大写)
str.capitalize() # Hello,lvshuai(仅仅句子的第一个单词首字母大写)
str.upper() # HELLO,LVSHUAI
str.lower() # hello,lvshuai
字符串格式化
"这是你的{0}{1}!".format("lv","shuai")
# 这是你的lvshuai!
"这是你的{1}{0}!".format("shuai","lv")
# 这是你的shuailv!
"我的名字:{name},我的电话:{tel}".format(name="lvshuai",tel="133333333")
#我的名字:lvshuai,我的电话:133333333
3.2数字
数字类型
type(5) # int
type(5.0) # float
数字格式化
| 数字 | 格式 | 输出 | 描述 |
|---|---|---|---|
| 3.1415926 | {:.2f} | 3.14 | 保留小数点后两位 |
| 3.1415926 | {:+.2f} | +3.14 | 带符号保留小数后两位 |
| -1 | {:+.2f} | -1.00 | 带符号保留小数后两位 |
| 2.1878 | {:.0f} | 3 | 不带小数 |
| 5 | {:0>2d} | 05 | 数字补零(填充左边,宽度为2) |
| 5 | {:x<4d} | 5xxxx | 数字补x(填充右边,宽度为4) |
| 1000000 | {:,} | 1,000,000 | 以逗号分隔的数字格式 |
| 0.25 | {:.2%} | 25.00% | 百分比格式 |
| 1000000000 | {:.2e} | 1.00e+09 | 指数记法 |
| 13 | {:10d} | 13 | 右对齐(默认,宽度为10) |
| 13 | {:<10d} | 13 | 左对齐(宽度为10) |
| 13 | {:^10d} | 13 | 中间对齐(宽度为10) |
print("{:.3f}".format(3.1415926))
# 3.142
3.3布尔型
- 变量
- True
- False
- 操作符
- == !=
- and or not
4.容器
容器:一种组织各种元素的数据结构。
4.1列表(lists)
用[]标识 ,元素之间用逗号隔开
创建列表
#1.range(),它返回的是一个range对象。
range(1,11)
#如何返回列表?
list(range(1,11))
得到[1,2,...,10]
#2.列表推导
格式:[变量的运算 for 变量 in 列表]
a=[1,2,3,4]
b=[i+1 for i in a]
pirnt(b)
得到[2,3,4,5]
列表元素操作
squares=[value**2 for value in range(1,11)]
print(squares)
# [1,4,9,16,25,36,49,64,81,100]
#元素个数 10
print(len(squares))
#最大元素 100
print(max(suqares))
#最小元素 1
print(min(squares))
#列表元素之和 385
print(sum(squares))
列表增删查改
#1.增
list.append("10")#在末尾增加"10"
list.insert(1,3)#在第二个位置插入3
#2.删
del list[0] #删除第一个元素
poped_Num=list.pop() #能够返回删除的元素,默认删除最后一个
list.pop(0)#也可以指定删除的索引
list.remove(4)#4是具体的值,而不是索引,如果4出现多次,那么只删除第一次出现的
#3.查
- in
- not in
- count
- index
a_list=['a','b','c']
print('a' in a_list)#True
print('a' not in a_list)#False
print(a_list.count('a'))#1 统计个数
print(a_list.index('a'))#0 索引位置
# 4.改
x=[1,2,3,4,5]
x[1]=0
print(x)
#[1,0,3,4,5]
切片(前闭后开)
[start:end:step]
- start:起始索引
- end:结束索引
- step:步长.步长为正,从左往右取值。步长为负,反向取值
squares=[1,4,9,16,25,36,49,64,81,100]
print(squares[0:3])# [1,4,9]
print(squares[:3])# [1,4,9]
print(squares[4:])# [25,36,49,64,81,100]
print(squares[-4:])# 从倒数第四个元素取[49,64,81,100]
print(squares[:-1])# 不包括最后一个[1,4,9,16,25,36,49,64,81]
4.2元组(dictionaries)
不可变的列表称为元组, 用()表示。
创建元组(和列表几乎一样)
MyTuple=(10,20,30,40,50)
print(MyTuple[3]) #40
## 注意!!
# 只有一个元素的tuple定义时必须加一个逗号,用来消除歧义
T=(1)
P=(1,)
print(type(T),type(P))
# 无法修改元素
MyTuple[0]=1;#报错
4.3字典(tuples)
其他语言中称为map,使用键-值(key-value)存储,具有很快的查找速度,空间换时间。 用{}来标识。
创建和添加
Agenda={
} # 空字典
Agenda={
'Monday':'shopping','Tuesday':'working'}
print(Agenda['Tuesday']) #working
# 添加键值对
Agenda['Sunday']='sleeping'
删除
pop(key)#将键放入括号
Agenda.pop('Tuesday')
4.4三个容器对比
- list、tuple是有序列表;dict是无序列表
- list元素可变,tuple元素不可变
- tuple的操作速度比tuple较快,安全性好
- dict的key值不可变,唯一性
- dict查询效率高,但消耗内存多;list、tuple查询效率低,但消耗内存少
5.流程控制
条件判断if、if else、if elif elif else
循环 while循环 for循环
for <var> in <sequence>:
<body>
<sequence>可以是列表,range()函数。
6.函数和类
函数的基本思想:写一个语句序列,并给这个序列取一个名字,然后可以通过引用函数名称,在程序中的任何位置执行这些指令。
# def是define的缩写。
类:相当于一个基因制造图纸。
class Animal(object):
#实例化时候会自动调用这个函数
# 通常用来对实例的属性进行初始化
def __init__(self,name):
self.name=name
...
class Pig(Animal):
#猪所特有的个性通过编写函数来覆盖Animal父类的对应的方法。
#没有覆盖的函数默认采用相同的方法
#实例化
pig1= Pig('猪')
#调用类中的方法
pig1.方法()
7.数值计算扩展库Numpy
思考:为什么用numpy? 后期深度学习需要通过矩阵计算数据,而列表很耗费内存,而numpy不仅可以将数据转换为矩阵形式,甚至是更高维度的数组。
0维数组是标量 1维数组是向量 2维数组是矩阵
7.1数组的创建
array()
# array中的数据类型必须相同
import numpy as np
vector=np.array([5,10,15,20])#一维数组
matrix=np.array([[5,10,15,20],[20,25,30,35],[35,40,45,50]])#二维数组
arange()
指定开始值、终止值和步长来创建等差数列的一维数组 注:所得到的结果中不包含终值
a=np.arange(0,1,0.1)
print(a)
# [0. 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9]
# 不包含终值1
zeros() ones()
Zerosvector=np.zeros([4,3],np.int)#4行3列的整型全零矩阵
Onesvector=no.ones([4,3],np.float)#4行3列的浮点型全一矩阵
7.2数组的形状
shape
# shape返回一个元组,元组的数字代表数轴各个轴的长度
# 1.查看
print(vector.shape)#(4,)
print(matrix.shape)#(3,4)
reshape
#2.修改形状
#2.1直接赋值
matrix.shape=4,3
print(matrix.shape)#(4,3)
#虽然维数改变了,但是元素在内存中位置没有改变
##如果某一个维数赋值为-1,会根据另一个维数自动计算
matrix.shape=-1,6
print(matrix.shape)#(2,6)
#2.2reshape()
# 创建新数组,原数组保持不变
matrix2=matrix.reshape(3,4)
matrix2
##新数组和原数组的数据是共享的,任何一个数组的数据修改,都会引起另一个数组相应的位置的数据的修改
7.3存取元素
和列表中的切片相似
a=np.arange(10)# a就是[0,1,2,3,4,5,6,7,8,9]
print(a)
#[0,1,2,3,4,5,6,7,8,9]
print(a[5])#相当于[0,1,2,3,4,5,6,7,8,9][5]
#5
print(a[3:5])
#[3,4]
print(a[:5])
#[0,1,2,3,4]
print(a[:-1])
#[0,1,2,3,4,5,6,7,8] 不包含倒数第一个
### 修改
a[2:4]=100,101
a
#array([0,1,100,101,4,5,6,7,8,9])
7.4加减乘除开方
#1.创建矩阵
x=np.array([[1,2],[3,4],dtype=np.float64)
x=np.array([[5,6],[7,8],dtype=np.float64)
#2.矩阵中的x+y x-y x*y x/y np.sqrt(x)都是元素的逐个运算
#3.矩阵相乘np.dot()
np.dot(x,y)
#4.数组中所有元素之和np.sum()
np.sum(x)
#5.转置矩阵
#原矩阵:
np.dot(x,y)
#转置矩阵:
np.dot(x,y).T
#6.广播机制
a=np.array([0,10,20,30]).reshape(4,1)#列向量
b=np.array([0,1,2]).reshape(1,3)#行向量
print(a+b)
8.二维绘图库Matplotlib
notebook中运行需要写入以下代码
%matplotlib inline
# 1.通过列表传输数据
import matplotlib.pyplot as plt
plt.plot([1,2,3,4])# 默认为y值。
#由于python中x从0开始,因此对应的是0,1,2,3
plt.show()
# x,y对应
plt.plot([1,2,3,4],[1,4,9,16])
# 等价于
plt.plot([1,2,3,4],[1,4,9,16],"b-")#蓝线
plt.plot([1,2,3,4],[1,4,9,16],"ro")#红点
plt.axis([0,6,0,20])#[xmin,xmax,ymin,ymax]
#2.通过numpy数组传输数据
import numpy as np
t=np.arange(0.,5.,0.2)
plt.plot(t,t,'r--',t,t**2,'bs',t,t**3,'g^')
plt.show()
# 对线宽修改setup()
import numpy as np
t=np.arange(0.,5.,0.2)
plt.plot(t,t,'r--',t,t**2,'bs',t,t**3,'g^')
plt.setup(lines,linewidth=5.0)
plt.show()
9.pytorch简介
深度学习计算和优化算法都是基于张量的
- 张量(是基于向量和矩阵的推广)
- 标量是零维的张量
- 矢量是一维的张量
- 矩阵是二维的张量
本次课程是图像迁移的项目,需要把图像数据集抽象成四阶的张量表示。 四个维度分别是
- 图片在数据集中的编号
- 图片的高度
- 宽度
- 色彩数据
深度学习框架可以从简单的数学运算到卷积和池化操作,不同的框架的张量操作有区别。
计算图将张量和面对张量的操作整合起来,输出结果。 使用不同的占位符构成了不同的操作节点。使用不同的字母构成了变量结点。通过有向线段把这些节点连接起来,共同组成了一个表针的数据结构。
自动求导。在深度学习中,通过梯度下降来更新模型的参数。如果模型过于复杂,手动进行梯度计算将十分困难,但自动求导可以使其自动化实现。
BLAS、cuBLAS、cuDNN等拓展包,提高运算效率。
Pytorch的优势:
- 简洁:tensor到变量到nn.Module这从低到高的三个抽象层次。
- 速度。
- 易用。
- 易调用。
10.pytorch的数据预处理工具:torchvision
简介
torchvision是一个图像操作工具库
- 数据处理
- 数据导入
- 数据预览
组成
- 模型models(训练好的)
- 数据集datasets:MNIST、CIFAR10/100、ImageNet、coco
- 数据预处理操作transforms
transforms
transforms可以解决数据类型转换与增强:
- 标准化:transforms.Normalize
- 图像数据转为tensor,并归一化至[0-1]:transforms.ToTensor
- 将数据转换为PILImage(数据处理完之后,在转换为图像):transforms.ToPILImage
- 对载入的图片数据大小进行缩放:transforms.Resize
- 对载入的图片进行裁剪:transforms.CenterCrop
transforms.Compose() 可以看做是一个容器,可以把多种数据变换进行组合
transform=transforms.Compose([transforms.ToTensor(),transforms.Normalize(mean=[0.5,0.5,0.5],std=[0.5,0.5,0.5])])
# 先转换为张量,再标准化即减去均值,除以标准差
11. 从生物神经网络到感知机
11.1生物神经网络
树突:信息输入端(类似树枝)
轴突:信息输出端(长长的轴突)
突触:本神经元和外部神经元之间的接口
神经元超过一定的阈值,会兴奋起来。
11.2感知机
O u t p u t 1 = w 1 x 1 + w 2 x 2 + w 3 x 3 O u t p u t 2 { = 0 , i f ( w 1 x 1 + w 2 x 2 + w 3 x 3 ) ≤ t h r e s h o l d = 1 , i f ( w 1 x 1 + w 2 x 2 + w 3 x 3 ) > t h r e s h o l d Output_1 = w_1x_1+w_2x_2+w_3x_3 Output_2\begin{cases} =0,if(w1x1+w2x2+w3x3)≤threshold\\ =1,if(w1x1+w2x2+w3x3)>threshold\\ \end{cases} Output1=w1x1+w2x2+w3x3Output2{ =0,if(w1x1+w2x2+w3x3)≤threshold=1,if(w1x1+w2x2+w3x3)>threshold
eg:
-
你想要的看樱花,你犹豫去还是不去,考虑以下三个因素:
-
天气好不好 x1(好1,不好0)
-
是否有时间去 x2(有1,没0)
-
交通是否方便 x3(是1,否0)
-
搭建感知机模型:
-
w1=6(权重)
-
w2=w3=2
-
threshold=5(阈值)
-
情景1:天气不好,有时间,交通便利 0 * 6 + 1 * 2 + 1 * 2=4<5–>output=0,不去!
-
情景2:天气好,没时间,交通不便利 1 * 6 + 0 * 2 + 0 * 2=6>5–>output=1,去!
简化描述
w ⋅ x = ∑ j w j ⋅ x j w·x=∑^jw_j·x_j w⋅x=∑jwj⋅xj
b = − t h r e s h o l d b=-threshold b=−threshold
O u t p u t { = 0 , i f w x + b ≤ 0 = 1 , i f w x + b > 0 Output\begin{cases} =0 ,if wx+b≤0\\ =1,if wx+b>0\\ \end{cases} Output{ =0,ifwx+b≤0=1,ifwx+b>0
O u t p u t = S g n ( w ⋅ x + b ) Output=Sgn(w·x+b) Output=Sgn(w⋅x+b)
sgn函数称为激活函数
12.从神经网络到深度学习
12.1神经网络
将感知机组成一层或多层的网络状结构就构成了神经网络。
- X1,X2,X3是输入、AB是第一层感知机、CD是第二层感知机,进而CD进行输出。
- (这个神经网络有四个感知机)
- 输入–>第一层感知机–>将第一层感知机的输出作为第二层感知机的输入–>第二层感知机–>第二层感知机输出。
浅层神经网络
S n g ( x ) − − > S i g m o i d ( x ) Sng(x)-->Sigmoid(x) Sng(x)−−>Sigmoid(x)
激活函数改成sigmoid解决了激活函数输出不连续、不光滑的问题。
深层神经网络
其他激活函数。
12.2深度学习
什么是模型?什么是算法?
模型是数学模型,通过数学符号建立起输入、输出的关系。(感知机、神经网络)
算法是求解具体问题时采用的方法。(计算感知机参数w的具体取值采用的计算方法)
深度学习定义:为了让层数较多的多层神经网络可以有效训练而演化的一系列新模型与新算法的总称。
- 新模型:CNN、LSTM、ResNet
- 新算法:权重初始化、新优化算法、防止过拟合
为什么深度学习会风靡?
- 大数据与分布式存储(如果深度学习是蒸汽机,数据就是燃料)
传统的机器学习模型随着数据量增加,性能会遇到瓶颈,那么就需要对模型本身改进或采用集成的方法从而提高性能。而深度学习只需要数据量足够大即可。
- GPU的并行计算
GPU存在大量核心,能并行运算,而CPU只有很少的核心。
- 算法的改进
20世纪末期,浅层神经网络的性能差于支持向量机、随机森林,而深层神经网络的多层叠加的梯度传播随着梯度增加,神经网络的反馈信号会消失。
但在2009-2010年,出现了重要的算法改进,实现了更好的梯度传播。
- 更好的神经层激活函数(activation function)
- 更好的权重初始化方案(weight-initialization scheme)
- 更好的优化方案(optimization scheme)
13.神经网路工作原理
目标:找到正确的权重;评价指标:损失函数(目标函数);方法:优化算法+反向传播算法
- 不希望输出除预测值以外:那么就需要的控制实际输出和预期值之间的距离,这就是损失函数。
- 损失函数:
I n p u t : 真 实 值 、 预 测 值 Input:真实值、预测值 Input:真实值、预测值
O u t p u t : 距 离 值 ( 衡 量 这 个 网 络 在 样 本 上 的 好 坏 ) Output:距离值(衡量这个网络在样本上的好坏) Output:距离值(衡量这个网络在样本上的好坏)
- 通过距离值作为反馈,来对权重进行微调,降低当前样本的损失值,这就是优化器实现的。
- 优化器实现的是反向传播算法,是深度学习的核心算法。
14.损失函数
深度学习的“学习”就是尽可能地在不过拟合的情况下降低损失值。
- L1损失函数(平均绝对误差函数,MAE):nn.L1Loss
- 均方误差函数(Mean Square Error,MSE):nn.MSELoss
- 交叉熵损失:nn.CrossEntropyLoss()(nn.LogSoftmax()+nn.NLLLoss())
- CrossEntropyLoss()是NLLLoss()的一个特例。
- 交叉熵描述的是两个概率分布的差异性,然而神经网络输出的向量,就需要logsoftmax函数将向量归一化,统一变成概率分布,在运用交叉熵损失。
import torch
from torch.autogard import Variable
import torch.nn as nn #损失函数。它也是一种层结构,因为用来构建神经网络层结构。
sample=Variable(torch.ones(2,2)) # 真实值,它是全1的张量,通过variable变成了变量
a= torch.Tensor(2,2)
a[0,0]=0
a[0,1]=1
a[1,0]=2
a[1,1]=3 #通过索引创建预测值
target=Variable(a) # 预测值(输出值)
print(sample)
print(target)
##希望输出值逼近真实值
# 1.L1损失函数
criterion=nn.L1Loss()
loss=criterion(sample,target)
print(loss)
# 2.均方误差函数
criterion=nn.MSELoss()
loss=criterion(sample,target)
print(loss)
#3.交叉熵损失--用于图像识别验证,对输入参数有要求
criterion=nn.CrossEntropyLoss()
loss=criterion(sample,target)# 错误
print(loss)
15.优化算法
15.1pytorch优化器
- 优化器的含义:计算导数的算法
- 优化器的目的:让用户选择一种适合自己场景的优化器
- 优化器的衡量指标:每一轮样本数据的优化都让权重参数匀速的接近目标值
- torch.optim
- SGD,Adam,Adadelta,Adagard,Adamax
15.2梯度下降原理
导数知识
设函数连续,那么x的微小变化会引起y的微小变化。即f(x+△x)=y+ △y
设函数光滑,可以将f近似为斜率为k的线性函数,即△y=k△x。即f(x+△x)=y+k△x
当x足够接近P,那么就能定义k为P点的导数,其大小代表了函数在这一点增加的速度的快慢
总结:对于y=f(x)求导,就是将x映射为y在该点的局部的线性的近似斜率。
从导数->偏导,就是从曲线->曲面的过程。
在曲线上的点,切线只有一条,在曲面上的点,切线有无数条。
偏导就是多元函数沿着坐标轴的变化率。(具有局限性,因为只能沿着xyz坐标轴)
为了结局上述问题,进行了推广,提出了“梯度”的概念,梯度就是对每个变量求微分,用逗号隔开,说了梯度是一个向量。向量具有方向,梯度的方向就指出了函数在指定点上升最快的方向。
梯度下降基本思想:下山的过程
为了下山,以当前所处位置为基准,找到这个位置最陡峭的地方,然后朝着沿着山高度下降的方向走,每走一段距离,都采用相同的方法,最终达到山谷。
将一个可以微分的函数比作这个山;找到了这个函数的最小值就是找到山谷;找到最陡峭的地方就是找到函数的梯度,沿着梯度相反的方向走,就能使函数下降最快。
数学解释
θ 1 = θ 0 − α J ( θ ) , e v a l u a t e d a t θ 0 θ^1=θ^0-αJ(θ),evaluated at θ^0 θ1=θ0−αJ(θ),evaluatedatθ0
从 θ^0 点走到J(θ)最小值。由于是反向,因此取-,步长为α,走到了 θ^1 。反复迭代。
如果步长过小,迭代次数过多,浪费计算资源。如果过大,那么可能会跳过最小点,导致函数无法收敛到最小值。因此如何选取步长呢?这就衍生出了优化算法。
15.3常用优化器分析
SGD:随机梯度下降
和梯度下降的区别是:梯度下降需要拿来全部数据一次性处理,而随机梯度下降是随机选取部分数据参与计算。适用于数据量大、数据有很多相似样本的情况。
torch.optim.SGD(params,Ir=0.01,momentum=0,dampening=0,weight_decay=0,nesterov=False)
#Ir:大于0的浮点数,学习率。
#momentum:大于0的浮点数,动量参数。
#动量类比于物理中,增大动量帮他跳出局部最小值。
#parameters:Variable参数,要优化的对象。
Adagrad:自动变更学习速率
缺点:需要设置全局变化率。造成深度很深的情况下,训练提前结束。
torch.optim.Adagrad(params,Ir=0.01,Ir_decay=0,weight_decay=0,initial_accumulator_value=0)
RMSprop:对Adagrad的一种改进
采用均方根作为分母,缓解adagrad学习率太快的问题,减少摆动
torch.optim.RMSprop(params,Ir=0.01,alpha=0.99,eps=1e-08,weight_decay=0,momentum=0,centered=False)
Adam:默认的优化算法
每次参数迭代步长都有明确的范围,不会因为很大的梯度导致很大的学习步长。参数更加稳定。本质上是带有动量项的RMS。优点:通过偏置矩阵,每次迭代学习率有一个明确的范围。
#amsgrad=True表示采用这个优化算法,否则不采用,它是添加额外的约束,使得学习率为正值。(2018顶会文章on the convergence of Adam and beyond)
torch.optim.Adam(params,Ir=0.001,betas(0.9,0.999),eps=1e-08,weight_decay=0,amsgrad=False)
16.反向传播算法
反向传播算法是深度学习的核心,求梯度是反向传播算法的核心。
16.1计算图
计算图:定义需要求导的函数,是特殊的有向无环图,记录算子和变量的关系。
- 矩形表示算子
- 椭圆形表示变量
e g : z = w x + b − > z = y + b ( y = w x ) eg:z=wx+b->z=y+b(y=wx) eg:z=wx+b−>z=y+b(y=wx)
其中,w,x,b成为叶子结点,z称为根节点。
2.链式求导
∂ z ∂ b = 1 \frac{∂z}{∂b}=1 ∂b∂z=1
∂ z ∂ x = ∂ z ∂ y ∗ ∂ y ∂ x = 1 ∗ w = w \frac{∂z}{∂x}=\frac{∂z}{∂y}*\frac{∂y}{∂x}=1*w=w ∂x∂z=∂y∂z∗∂x∂y=1∗w=w
∂ z ∂ w = ∂ z ∂ y ∗ ∂ y ∂ w = 1 ∗ x = x \frac{∂z}{∂w}=\frac{∂z}{∂y}*\frac{∂y}{∂w}=1*x=x ∂w∂z=∂y∂z∗∂w∂y=1∗x=x
3.计算图的反向传播
16.2反向传播
- 作用:对模型中的参数进行微调
- 本质:复合函数求导的过程
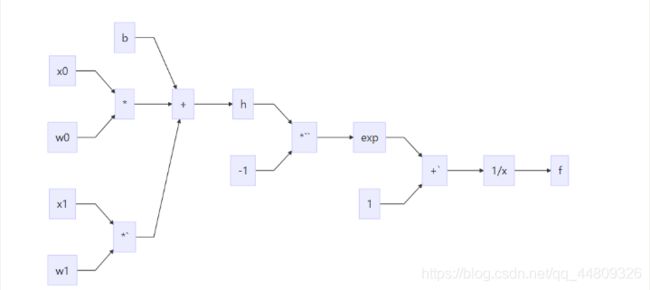
eg:初级神经网络的复合函数表达式:
f = 1 1 + e − ( w 0 x 0 + w 1 x 1 + b ) f = \frac{1}{1+e^{-(w0x0+w1x1+b)}} f=1+e−(w0x0+w1x1+b)1
x 0 = 1.5 , x 1 = 0.5 , b = − 1 , w 0 = 0.5 , w 1 = 0.5 x_0=1.5,x_1=0.5,b=-1,w_0=0.5,w_1=0.5 x0=1.5,x1=0.5,b=−1,w0=0.5,w1=0.5
代 入 的 f = 0.5 代入的f=0.5 代入的f=0.5
计算图:
求导过程:
f ( w 0 , w 1 ) f(w0,w1) f(w0,w1)
令 h = w 0 x 0 + w 1 x 1 + b 令h=w_0x_0+w_1x_1+b 令h=w0x0+w1x1+b
得 f ( h ) = 1 1 + e − h = 0.5 得f(h)=\frac{1}{1+e^{-h}}=0.5 得f(h)=1+e−h1=0.5
w 0 的 反 向 传 播 微 调 值 : ∂ f ∂ w 0 = ∂ f ∂ h ∗ ∂ h ∂ w 0 = ( 1 − f ( h ) ) f ( h ) ∗ 1.5 = ( 1 − 0.5 ) ∗ 0.5 ∗ 1.5 = 0.375 w0的反向传播微调值: \frac{∂f}{∂w_0}=\frac{∂f}{∂h}*\frac{∂h}{∂w_0}=(1-f(h))f(h)*1.5=(1-0.5)*0.5*1.5=0.375 w0的反向传播微调值:∂w0∂f=∂h∂f∗∂w0∂h=(1−f(h))f(h)∗1.5=(1−0.5)∗0.5∗1.5=0.375
w 1 的 反 向 传 播 微 调 值 : ∂ f ∂ w 1 = ∂ f ∂ h ∗ ∂ h ∂ w 1 = ( 1 − f ( h ) ) f ( h ) ∗ 0.5 = ( 1 − 0.5 ) ∗ 0.5 ∗ 0.5 = 0.125 w1的反向传播微调值: \frac{∂f}{∂w_1}=\frac{∂f}{∂h}*\frac{∂h}{∂w_1}=(1-f(h))f(h)*0.5=(1-0.5)*0.5*0.5=0.125 w1的反向传播微调值:∂w1∂f=∂h∂f∗∂w1∂h=(1−f(h))f(h)∗0.5=(1−0.5)∗0.5∗0.5=0.125
补充:
f ( x ) = 1 1 + e − x f ′ ( x ) = 1 1 + e − x − 1 ( 1 + e − x ) 2 = f ( x ) ( 1 − f ( x ) ) f(x) = \frac{1}{1+e^{-x}} f\prime(x)=\frac{1}{1+e^{-x}}-\frac{1}{(1+e^{-x})^2}=f(x)(1-f(x)) f(x)=1+e−x1f′(x)=1+e−x1−(1+e−x)21=f(x)(1−f(x))
16.3atuograd-自动求导
- atuograd中的variable为我们提供了自动求导的功能。它的值会不断变化,类似于装鸡蛋的篮子,鸡蛋数会不断发生变化,这个鸡蛋就是tensor。
- torch.autograd.Variable
- 将tensor变为variable:variable(tensor)
- variable是加强版tensor,包含三个属性:
- data:保存variable所包含的tensor
- grad:保存data对应的导数值,其本身也是variable,它与data的形状是一样的。
- grad_fn:指向一个function,记录variable的操作历史。
- 在反向传播中,variable需要缓存原来的tensor来计算微分,如果需要计算各个variable的微分,只需要调入根节点的variable的datawork方法。
eg:如何自动求导?还以z=wx+b为例
import torch as t
from torch.autograd import Variable
# 首先,创建variable,也就是计算图中的叶子节点
x=Variable(t.Tensor([1]),requires_grad=True)# 赋值为1
w=Variable(t.Tensor([2]),requires_grad=True)
b=Variable(t.Tensor([3]),requires_grad=True)
# 然后,构建计算图
z = w*x+b # z=2x+3 相当于计算x=1时的导数值
# 自动求导
z.backward()
# 打印导数值
print(x.grad)# tensor([2,])
print(w.grad)# tensor([1,])
print(b.grad)# tensor([1,])
17.激活函数
多层神经网络下的线性模型表达式(无激活函数)
f ( x ) = W 3 ∗ ( W 2 ∗ ( W 1 ∗ X + b 1 ) + b 2 ) + b 3 f(x)=W3*(W2*(W1*X+b1)+b2)+b3 f(x)=W3∗(W2∗(W1∗X+b1)+b2)+b3
无论加深到多少层,图像始终是线性的,对非线性问题存在局限性。
非线性模型(有激活函数,以激活函数max为例)
f ( x ) = m a x ( W 2 ∗ ( m a x ( W 1 ∗ X + b 1 , 0 ) + b 2 , 0 ) f(x)=max(W2*(max(W1*X+b1,0)+b2,0) f(x)=max(W2∗(max(W1∗X+b1,0)+b2,0)
选取不同的非线性模型激活函数,便可以得到复杂多变的深度神经网络,处理更加复杂的问题。
常见的激活函数
Sigmoid数学表达式:
S i g m o i d 数 学 表 达 式 : f ( x ) = 1 1 + e − x Sigmoid数学表达式:f(x)=\frac{1}{1+e^{-x}} Sigmoid数学表达式:f(x)=1+e−x1
输出区间为(0,1),导数取值区间为(0,0.25)。 x越大,y越接近1.x越小,y越接近0. x过大过小,y`都接近0.
1.如果每层神经网络,都用sigmoid作为激活函数。那么反向传播过程中,没经过一个节点,都要乘上一个sigmoid导数值在(0,.025)之间。多次相乘后,梯度会变得非常小,甚至消失。
2.sigmoid的函数图像在两边收敛速度很慢,耗费时间。因此要尽量选取0中心附近的点。
sigmoid函数的导数图像中间高,两边低,梯度消失。
sigmoid函数的输出值恒大于0,模型在优化过程中学习速率变慢,时间成本高。
t a n h 的 数 学 表 达 式 : f ( x ) = e x − e − x e x + e − x tanh的数学表达式:f(x)=\frac{e^x-e^{-x}}{e^x+e^{-x}} tanh的数学表达式:f(x)=ex+e−xex−e−x
解决了模型优化过程中收敛速度过慢的问题,但是导数区间仍然是[0,1],在两边会出现梯度消失的情况。
R e L U ( 线 性 纠 正 单 元 ) 的 数 学 表 达 式 : f ( x ) = m a x ( 0 , x ) ReLU(线性纠正单元)的数学表达式:f(x)=max(0,x) ReLU(线性纠正单元)的数学表达式:f(x)=max(0,x)
使用广泛,收敛速度快,计算效率高。但输出并不是零中心数据,可能导致某些神经元永远不可能被激活,那么神经元的对应参数不能被更新。解决方法是:
- 使用更高级的初始化方法(Xavier)
- 设置合理的向后传播学习速率(Adam)
- 采用Leaky-ReLU、R-ReLU.
- Leaky-RuLU解决了函数右侧的0,改为-0.1、-0.2
import torch.nn as nn
import torch.autograd.variable as V
import torch as t
relu = nn.RELU(inplace=True)
input=V(t.randn(2,3))
print(input)
output=relu(input)
print(output)
18.卷积神经网络基础
用来处理图像。
全连接前馈网络图像存在的问题:
- 参数太多
- 局部不变性特征
卷积神经网络(CNN)的灵感来源:生物学的感受野机制
- 结构:卷积层、池化层、全连接层以及最后的sotfmax交叉堆叠而成,使用反向传播算法训练。
- 特性:局部连接,权重共享以及汇聚
- 优势:参数更少
卷积层
- 作用:对输入的数据进行特征提取
- 核心:卷积核
卷积核的定义及工作原理
eg:
输入图像:32x32x3(高、宽、RGB通道)
定义卷积核5x5x3(高、宽、深度)
卷积核的高、宽要比图像小,一般是5x5或者3x3
卷积通用公式
W o u t p u t = W i n p u t − W f i l t e r + 2 P S + 1 W_{output}=\frac{W_{input}-W_{filter}+2P}{S}+1 Woutput=SWinput−Wfilter+2P+1
H o u t p u t = H i n p u t − H f i l t e r + 2 P S + 1 H_{output}=\frac{H_{input}-H_{filter}+2P}{S}+1 Houtput=SHinput−Hfilter+2P+1
filter为卷积核参数,S为步长,P表示图像边界像素添加的层数filte**r为卷积核参数,S为步长,P表示图像边界像素添加的层数
步长就是卷积核经过一次滑动后窗口位置发生的变化。
图像边界添加层数有利于提升卷积效果的边界像素填充方式,让输入图像的全部像素都能尽量多的被滑动窗口捕捉到。
池化层
提取数据核心特征的方式
- 数据压缩
- 减少参数
池化层方法
- 最大池化层
- 平均池化层
池化通用公式
W o u t p u t = W i n p u t − W f i l t e r S + 1 W_{output}=\frac{W_{input}-W_{filter}}{S}+1 Woutput=SWinput−Wfilter+1
W o u t p u t = W i n p u t − W f i l t e r S + 1 W_{output}=\frac{W_{input}-W_{filter}}{S}+1 Woutput=SWinput−Wfilter+1
全连接层
作用:
- 将输入图像在经过卷积和池化操作后提取特征进行压缩
- 根据压缩的特征完成模型的分类功能
19.卷积神经网络模型
LeNet
- 结构简单,共七层。2层卷积、2层池化(两个交替出现)、3层全连接层。
import torch
import torch.nn as nn
import time
from torch.utils.data import DataLoader
from torchvision.datasets import MNIST
from torchvision import transforms
from torch import optim
#MNIST数据来自美国国家标准与技术研究所,National Institute of Standards and Technologu(NIST).训练集(training set)由来自250个不同人手写的数字构成。其中50%是高中生,50%是人口普查局(the Census Bureau)的工作人员. 测试集(test set)也是相同比例的手写数字数据
def loadMNIST(batch_size): #MNIST图片的大小是28*28
trans_img=transforms.Compose([transforms.ToTensor()])
trainset=MNIST('./data',train=True,transform=trans_img,download=True)
testset=MNIST('./data',train=False,transform=trans_img,download=True)
trainloader=DataLoader(trainset,batch_size=batch_size,shuffle=True,num_workers=10)
testloader=DataLoader(testset,batch_size=batch_size,shuffle=False,num_workers=10)
return trainset,testset,trainloader,testloader
#Letnet卷积神经网络
class Lenet(nn.Module):
def __init__(self):
super(Lenet,self).__init__()
layer1=nn.Sequential()# 第一层
layer1.add_module('conv1',nn.Conv2d(1,6,5,padding=1))# 输入一张图 输出六张特征图。卷积核大小为5x5
layer1.add_module('acl',nn.ReLU())# 激活函数
layer1.add_module('pool1',nn.MaxPool2d(2,2))#池化层2x2
self.layer1=layer1
layer2=nn.Sequential()# 第二层
layer2.add_module('conv2',nn.Conv2d(6,16,5,padding=1))# 输入六个通道,输出16张特征图。卷积核大小为5x5
layer2.add_module('acl',nn.ReLU())
layer2.add_module('pool2',nn.MaxPool2d(2,2))
self.layer2=layer2
#全连接层
layer3=nn.Sequential()
layer3.add_module('fc1',nn.Linear(400,120))
layer3.add_module('ac1',nn.ReLU())
layer3.add_module('fc2',nn.Linear(120,84))
layer3.add_module('ac2',nn.ReLU())
layer3.add_module('fc3',nn.Linear(84,10))#得到10个参数对应了0,1...9
self.layer3=layer3
def forward(self,x):
x=self.layer1(x)
x=self.layer2(x)
x=x.view(x.size(0),-1)
x=self.layer3(x)
return x
if __name__=='__main__':
t_start=time.time()
learning_rate=0.001# 学习率,保持梯度在一定范围
batch_size=200#训练集200个,一次200个
epoches=50#循环次数
lenet = Lenet()#network
trainset,testset,trainloader,testloader=loadMNIST(batch_size)#data
criterian=nn.CrossEntropyLoss(reduction='sum')#求和的方式计算loss
optimizer=optim.SGD(lenet.parameters(),lr=learning_rate)#optimizer
for i in range(epoches):
running_loss=0.
running_acc=0.
for (img,label) in trainloader:#替换训练集
optimizer.zero_grad()# 求梯度之间对梯度清零以防梯度累加
output=lenet(img)#前向计算网络输出值
loss=criterian(output,label)#计算loss值
loss.backward()#loss反传存到相应的变量结构中
optimizer.step()#使用计算好的梯度对参数进行更新
running_loss+=loss.item()
valu,predict=torch.max(output,1)
correct_num=(predict==label).sum()
running_acc+=correct_num.item()
running_loss/=len(trainset)
running_acc/=len(trainset)
t_now=time.time()
time_spend=t_now-t_start
print("[%d/%d] Loss:%.5f, Acc:%.2f,Time:%.2f"%(i+1,epoches,running_loss,
100*running_acc,time_spend))
VGGNet
- 真正意义上深层网络结构
- 堆叠卷积层和池化层
vgg几乎全部使用3x3的卷积核以及2x2的池化层,使用小的卷积核进行多层的堆叠和一个大的卷积核的感受野是相同的,同时小的卷积核还能减少参数,可以有更深的结构;vgg的关键就是使用很多层3x3的卷积然后再使用一个最大池化层,这个模块被使用了很多次
import time
import sys
sys.path.append('..')
import numpy as np
import torch
import utils
from torch import nn
from torch.autograd import Variable
from torchvision.datasets import CIFAR10
# 卷积层的生成函数;卷积模块,多个卷积层,一个池化层
def vgg_block(num_convs,in_channels,out_channels):
net=[nn.Conv2d(in_channels,out_channels,kernel_size=3,padding=1),nn.ReLU(True)]
for i in range(num_convs-1):
net.append(nn.Conv2d(out_channels,out_channels,kernel_size=3,padding=1))
net.append(nn.ReLU(True))
net.append(nn.MaxPool2d(2,2))
return nn.Sequential(*net)
block_demo=vgg_block(3,64,128)# 3个卷积层,64通道输入,128通道输出
print(block_demo)
#--------------------------
input_demo=Variable(torch.zeros(1,64,300,300))#300x300像素,64通道
output_demo=block_demo(input_demo)
print(output_demo.shape)#输出128通道 150x150图像。起到了压缩作用
#--------------------------
# 多个卷积模块相叠加
def vgg_stack(num_convs,channels):#卷积模块数,通道参数
net=[]
for n,c in zip(num_convs,channels):
in_c=c[0]
out_c=c[1]
net.append(vgg_block(n,in_c,out_c))
return nn.Sequential(*net)
# 5个卷积模块,每个卷积模块有多个卷积层 3层输入-->512输入
vgg_net=vgg_stack((1,1,2,2,2),((3,64),(64,128),(128,256),(256,512),(512,512)))
print(vgg_net)
#--------------------------
test_x=Variable(torch.zeros(1,3,256,256))
test_y=vgg_net(test_x)
print(test_y.shape)
#---------------------------
# 卷积层和全连接层相连
class vgg(nn.Module):
def __init__(self):
super(vgg,self).__init__()
self.feather=vgg_net
self.fc=nn.Sequential(
nn.Linear(512,100),
nn.ReLU(True),
nn.Linear(100,10)#512个参数转换为10参数
)
def forward(self,x):
x=self.feather(x)
x=x.view(x.shape[0],-1)
x=self.fc(x)
return x
def data_tf(x):
x=np.array(x,dtype='float32')/255
x=(x-0.5)/0.5
x=x.transpose(2,0,1)
x=torch.from_numpy(x)
return x
# 用数据集训练测试模型效果
# CIFAR-10是一个更接近普适物体的彩色图像数据集。CIFAR-10是由Hinton的学生整理
# 用于识别普适物体的小型数据集。白一共包含10个类别的RGB彩色图片:飞机、鸟类、猫、
# 鹿、狗、蛙、马、船、卡车。尺寸为32x32,数据集中一共有50000张训练图片和10000测试图片。
train_set=CIFAR10('./data',train=True,transform=data_tf,download=True)
train_data=torch.utils.data.DataLoader(train_set,batch_size=64,shuffle=True)
test_set=CIFAR10('./data',train=False,transform=data_tf,download=True)
test_data=torch.utils.data.DataLoader(test_set,batch_size=128,shuffle=False)
net=vgg()
optimizer=torch.optim.SGD(net.parameters(),lr=0.001)# 传播函数
criterian=nn.CrossEntropyLoss()# 损失函数
#--------------------
t_start=time.time()
epoches=20
for i in range(epoches):
running_loss=0.
running_acc=0.
for (img,label) in train_data:#替换训练集
optimizer.zero_grad()# 求梯度之间对梯度清零以防梯度累加
output=net(img)#前向计算网络输出值
loss=criterian(output,label)#计算loss值
loss.backward()#loss反传存到相应的变量结构中
optimizer.step()#使用计算好的梯度对参数进行更新
running_loss+=loss.item()
valu,predict=torch.max(output,1)
correct_num=(predict==label).sum()
running_acc+=correct_num.item()
running_loss/=len(trainset)
running_acc/=len(trainset)
t_now=time.time()
time_spend=t_now-t_start
print("[%d/%d] Loss:%.5f, Acc:%.2f,Time:%.2f"%(i+1,epoches,running_loss,
100*running_acc,time_spend))
20.图像风格迁移原理
给定原始图片,并选择艺术家的风格图片,就能把原始图片转化成具有相应艺术家风格的图片
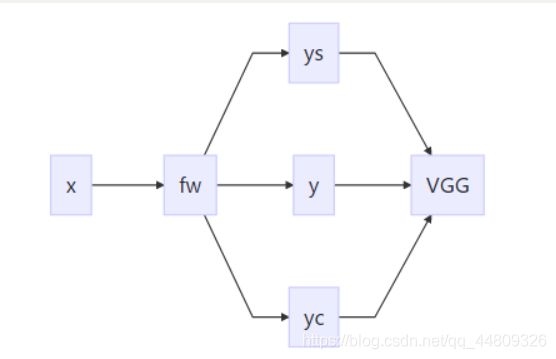
Fast Neural Style.
x是输入图像。Image Transform Net(fw)是设计的风格与迁移网络。返回一张图像y,y在图像内容上与yc相似,在风格上与ys相似。lossnetwork损失网络采用ImageNet上预训练好的VGG-16。
VGG-16
VGG-16网络从左到右有五个卷积块,每个卷积块有卷积层、激活函数、池化层。通过不断的提取特征值,图像的特征被提取的越来越详细、精准。
两个卷积块之间通过maxpooling层区分,每个卷积块有2-3个卷积层,每一个卷积层后面都跟着一个ReLU激活层。relu2-2表示第二个卷积块的第2个卷积层的激活层的输出。
该算法的本质是利用深度卷积网络对图像输入的抽象:
- 将风格图像输入卷积神经网络,将某些层输出作为风格特征。
- 将内容图像输入卷积神经网络,将某些层输出作为内容特征。
- 不断优化一个随机图像,使得它在该卷积神经网络的对应层输出不断接近上述两个图像的风格和内容特征(迭代)。
21.图像风格迁移实战
- 预训练模型VGG19,是在imagenet数据集上预训练的模型,它学习到的是对图像特征的提取方法,理论上也可以直接用于抽取其它图像的特征,这就是迁移学习及基础。
- 模型设计得到损失函数,从而反向传播优化。输入层要设置variable,输入一张噪声照片,根据内容loss和风格loss对其调整,达到一定次数,输入层的参数就是我们生成的图片。

损失函数计算
- 内容损失函数。这里使用内容图片在指定层上提取出的特征矩阵,与噪声图片在对应层上的特殊矩阵的差值的平方。即求两两之间的像素差值的平方。
L i = 1 2 ∗ M ∗ N ∑ i j ( X i j − P i j ) 2 L_i=\frac{1}{2*M*N}\sum_{ij}(X_{ij}-P_{ij})^2 Li=2∗M∗N1ij∑(Xij−Pij)2
- 格拉姆矩阵。n维欧式空间中任意k个向量之间两两的内积所组成的矩阵,称为这k个向量的格拉姆矩阵(Gram matrix)简单来说就是内积可以反映出两个向量之间的某种关系。Gram矩阵是两两向量的内积组成的,所以Gram矩阵可以反映出该组向量中各个向量之间的某种关系。
- 风格损失函数。这里使用风格图像在指定层上的特征矩阵的GRAM矩阵来衡量其风格,风格损失可以定义为风格图像和噪音图像特征矩阵的格莱姆矩阵的差值的平方。
L i = 1 4 ∗ M 2 ∗ N 2 ∑ i j ( G i j − A i j ) 2 L_i=\frac{1}{4*M^2*N^2}\sum_{ij}(G_{ij}-A_{ij})^2 Li=4∗M2∗N21ij∑(Gij−Aij)2
训练过程
- 指定部分层的输出来表示图片的内容特征和风格特征。
- 将内容图片输入网络,计算内容图片在网络指定层上的输出值。
- 计算内容损失和风格损失。
- 最终用于训练的损失函数为内容损失和风格损失的加权和。
- 训练开始时,我们根据内容图片和噪声,生成一张噪声图片。然后不断训练,直至迭代出最终效果。
from __future__ import print_function
import torch
import torch.nn as nn
from torch.autograd import Variable
import torch.optim as optim
from PIL import Image
import matplotlib.pyplot as plt
import torchvision.transforms as transforms
import torchvision.models as models
import copy
#---
use_cuda=torch.cuda.is_available()
dtype=torch.cuda.FloatTensor if use_cuda else torch.FloatTensor
#---
imsize=256 if use_cuda else 128 # use small size if no gpu
loader=transforms.Compose([
transforms.Scale(imsize),# scale imported image
transforms.ToTensor()]) # transform it into a torch tensor
def image_loader(image_name):
image=Image.open(image_name)
image=Variable(loader(image))
# fake.batch dimension required to fit network's input dimensions
image=image.unsqueeze(0)
return image
style_img=image_loader('images/water.jpg').type(dtype)
content_img=image_loader('images/fengjing.jpg').type(dtype)
assert style_img.size()==content_img.size(), \
"we need to import style and content images of the same size "
#---
# 图像加载器
unloader=transforms.ToPILImage() #reconvert into PIL image
plt.ion()
def imshow(tensor,title=None):
image=tensor.clone().cpu() # we clone the tensor to not do changes on it
image=image.view(3,imsize,imsize)# remove the fake batch dimension
image=unloader(image)
plt.imshow(image)
if title is not None:
plt.title(title)
plt.pause(0.001)# pause a bit as that plots are updated
plt.figure()
imshow(style_img.data,title='Style Image')
plt.figure()
imshow(content_img.data,title='Content Image')
#---
class ContentLoss(nn.Module):
def __init__(self,target,weight):
super(ContentLoss,self).__init__()
self.target=target.detach()*weight
self.weight=weight
self.criterion=nn.MSELoss()# 计算方法
def forward(self,input):
self.loss=self.criterion(input*self.weight,self.target)
self.output=input
return self.ouput
def backward(self,retain_graph=True):
self.loss.backward(retain_graph=retain_graph)
return self.loss
#---
# 格拉姆矩阵
class GramMatrix(nn.Module):
def forward(self,input):
a,b,c,d=input.size()
features=input.view(a*b,c*d)
G=torch.mm(features,features.t())
return G.div(a*b*c*d)
#---
class StyleLoss(nn.Module):
def __init__(self,target,weight):
super(StyleLoss,self).__init__()
self.target=target.detach()*weight
self.weight=weight
self.gram=GramMatrix()
self.criterion=nn.MSELoss()
def forward(self,input):
self.output=input.clone()
self.G=self.gram(input)
self.G.mul_(self.weight)
self.loss=self.criterion(self.G,self.target)
return self.output
def backward(self,retain_graph=True):
self.loss.backward(retain_graph=retain_graph)
return self.loss
#---
cnn=models.vgg19(pretrained=True).features
if use_cuda:
cnn=cnn.cuda()
#---
list(cnn)
#---
# 内容损失函数的计算层以及风格损失函数的计算层
content_layers_default=['conv_3']
style_layers_default=['conv_1','conv_2','conv_3','conv_4','conv_5']
def get_style_model_and_losses(cnn,style_img,content_img,
style_weight=1000,content_weight=1,
content_layers=content_layers_default,
style_layers=style_layers_default):
cnn=copy.deepcopy(cnn)
content_losses=[]
style_losses=[]
model=nn.Sequential()
gram=GramMatrix()
#move these modules to the GPU if possible:
# if use_cuda:
# model=model.cuda()
# gram=gram.cuda()
i=1
for layer in list(cnn):
if isinstance(layer,nn.Conv2d):
name="conv_"+str(i)#卷积层
model.add_module(name,layer)
#找到内容损失函数层
if name in content_layers:
# add content loss:
target =model(content_img).clone()
content_loss=ContentLoss(target,content_weight)
model.add_module("content_loss_"+str(i),content_loss)
content_losses.append(content_loss)
#找到风格损失函数层
if name in style_layers:
# add style loss:
target_feature =model(style_img).clone()
target_feature_gram=gram(target_feature)
style_loss=StyleLoss(target_feature_gram,style_weight)
model.add_module("style_loss_"+str(i),style_loss)
style_losses.append(style_loss)
if isinstance(layer,nn.ReLU):
name="relu_"+str(i)
model.add_module(name,layer)
i+=1
if isinstance(layer,nn.MaxPool2d):
name ="pool_"+str(i)
model.add_module(name,layer)
return model,style_losses,content_losses
#---
# 将内容图像作为输入
input_img=content_img.clone()
plt.figure()
imshow(input_img.data,title="Input Image")
#---
# 反向传播优化器
def get_input_param_optimizer(input_img):
# this line to show that input is a parameter that requires a gradient
input_param=nn.Parameter(input_img.data)
optimizer=optim.LBFGS([input_param])
return input_param,optimizer
#---
# 串联函数,定义整体框架
def run_style_transfer(cnn,content_img,style_img,input_img,num_steps=200,#200次
style_weight=1000,content_weight=1):
"""run the style transfer"""
print('Building the style transfer model..')
model,style_losses,content_losses=get_style_model_and_losses(cnn,style_img,content_img,style_weight,content_weight)
input_param,optimizer=get_input_param_optimizer(input_img)
print('Optimizing..')
run=[0]
while run[0]<=num_steps:
def closure():
# correct the values of updated input image
input_param.data.clamp_(0,1)
optimizer.zero_grad()
model(input_param)
style_score=0
content_score=0
#反向传播优化
for sl in style_losses:
style_score+=sl.backward()
for cl in content_losses:
content_score+=cl.backward()
run[0]+=1
if run[0]%50==0:
print("run{}:".format(run))
print("Style Loss:{:4f} Content Loss:{:4f}".format
(style_score.data,content_score.data))
print()
return style_score+content_score
optimizer.step(closure)
# a last correction..
input_param.data.clamp_(0,1)
return input_param.data# 将输出作为输入反复迭代
#---
output= run_style_transfer(cnn,content_img,style_img,input_img)
plt.figure()
imshow(output,title='Output Image')
# sphinx_gallery_thumbnail_number=4
plt.ioff()
plt.show()
#---
torch.cuda.empty_cache()