【LeetCode】153.寻找旋转排序数组中的最小值 (二分查找,java实现)
题目
链接
分析
方法一:暴力法
class Solution {
public int findMin(int[] nums) {
int start=0,end=nums.length-1;
while(start<end){
if(nums[start]>nums[end])
start++;
else end--;
}
return nums[start];
}
}
方法二:二分查找
解释一:与数组第一个数比较
一种暴力的解法是搜索整个数组,找到其中的最小元素,这样的时间复杂度是 O(N)O(N) 其中 NN 是给定数组的大小。
一个非常棒的解决该问题的办法是使用二分搜索。在二分搜索中,我们找到区间的中间点并根据某些条件决定去区间左半部分还是右半部分搜索。
由于给定的数组是有序的,我们就可以使用二分搜索。然而,数组被旋转了,所以简单的使用二分搜索并不可行。
在这个问题中,我们使用一种改进的二分搜索,判断条件与标准的二分搜索有些不同。
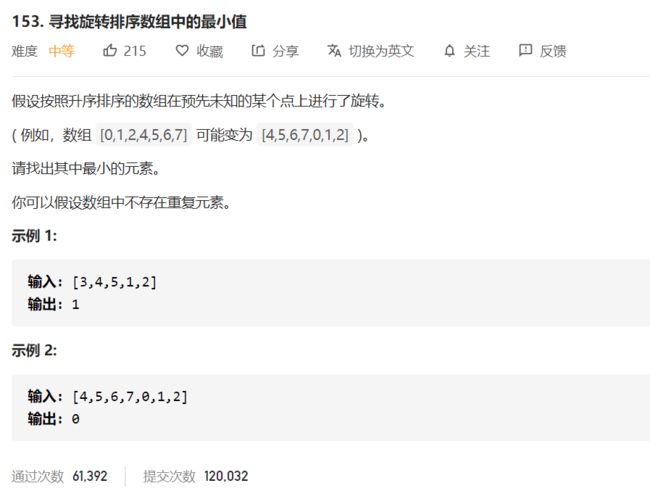
我们希望找到旋转排序数组的最小值,如果数组没有被旋转呢?如何检验这一点呢?
如果数组没有被旋转,是升序排列,就满足 last element > first element。
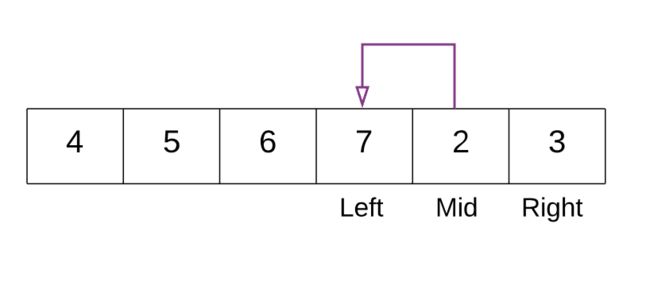
上图例子中 7>2 。说明数组仍然是有序的,没有被旋转。
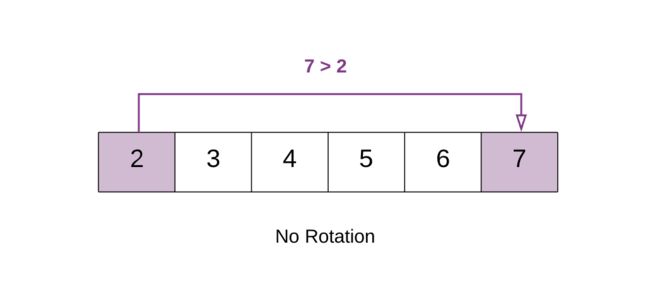
上面的例子中 3 < 4,因此数组旋转过了。这是因为原先的数组为 [2, 3, 4, 5, 6, 7],通过旋转较小的元素 [2, 3] 移到了后面,也就是 [4, 5, 6, 7, 2, 3]。因此旋转数组中第一个元素 [4] 变得比最后一个元素大。
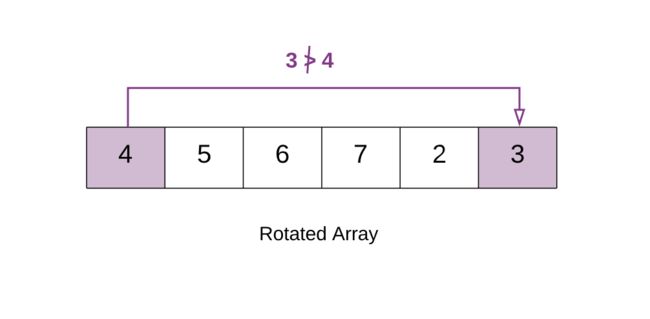
这意味着在数组中你会发现一个变化的点,这个点会帮助我们解决这个问题,我们称其为变化点。
在这个改进版本的二分搜索算法中,我们需要找到这个点。下面是关于变化点的特点:
所有变化点左侧元素 > 数组第一个元素
所有变化点右侧元素 < 数组第一个元素
算法
- 找到数组的中间元素
mid。 - 如果
中间元素 > 数组第一个元素,我们需要在mid右边搜索变化点。 - 如果
中间元素 < 数组第一个元素,我们需要在mid做边搜索变化点。
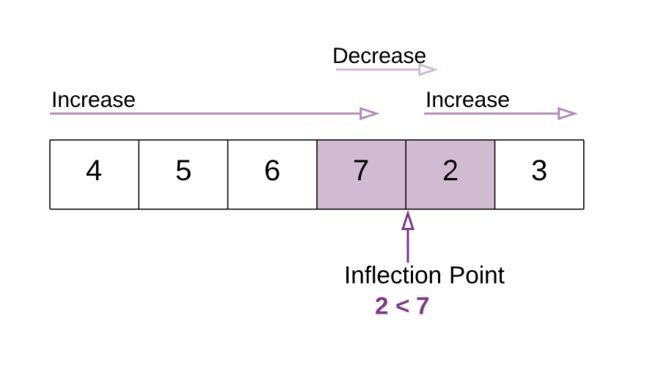
上面的例子中,中间元素 6 比第一个元素 4 大,因此在中间点右侧继续搜索。
- 当我们找到变化点时停止搜索,当以下条件满足任意一个即可:
nums[mid] > nums[mid + 1],因此 mid+1 是最小值。
nums[mid - 1] > nums[mid],因此 mid 是最小值。
在上面的例子中,标记左右区间端点。中间元素为 2,之后的元素是 7 满足 7 > 2 也就是 nums[mid - 1] > nums[mid]。因此找到变化点也就是最小元素为 2。
class Solution {
public int findMin(int[] nums) {
// If the list has just one element then return that element.
if (nums.length == 1) {
return nums[0];
}
// initializing left and right pointers.
int left = 0, right = nums.length - 1;
// if the last element is greater than the first element then there is no rotation.
// e.g. 1 < 2 < 3 < 4 < 5 < 7. Already sorted array.
// Hence the smallest element is first element. A[0]
if (nums[right] > nums[0]) {
return nums[0];
}
// Binary search way
while (right >= left) {
// Find the mid element
int mid = left + (right - left) / 2;
// if the mid element is greater than its next element then mid+1 element is the smallest
// This point would be the point of change. From higher to lower value.
if (nums[mid] > nums[mid + 1]) {
return nums[mid + 1];
}
// if the mid element is lesser than its previous element then mid element is the smallest
if (nums[mid - 1] > nums[mid]) {
return nums[mid];
}
// if the mid elements value is greater than the 0th element this means
// the least value is still somewhere to the right as we are still dealing with elements
// greater than nums[0]
if (nums[mid] > nums[0]) {
left = mid + 1;
} else {
// if nums[0] is greater than the mid value then this means the smallest value is somewhere to
// the left
right = mid - 1;
}
}
return -1;
}
}
解释二:和最右边的值比较
这道寻找最小值的题目可以用二分查找法来解决,时间复杂度为O(logN),空间复杂度为O(1)。
看一下代码:
class Solution {
public int findMin(int[] nums) {
int left = 0;
int right = nums.length - 1;
while (left < right) {
int mid = left + (right - left) / 2;
if (nums[mid] > nums[right]) {
left = mid + 1;
} else {
right = mid;
}
}
return nums[left];
}
};
首先说一下主要思路:
单调递增的序列:
*
*
*
*
*
做了旋转:
*
*
*
*
*
用二分法查找,需要始终将目标值(这里是最小值)套住,并不断收缩左边界或右边界。
左、中、右三个位置的值相比较,有以下几种情况:
-
左值 < 中值, 中值 < 右值 :没有旋转,最小值在最左边,可以收缩右边界
右 中 左 -
左值 > 中值, 中值 < 右值 :有旋转,最小值在左半边,可以收缩右边界
左 右 中 -
左值 < 中值, 中值 > 右值 :有旋转,最小值在右半边,可以收缩左边界
中 左 右 -
左值 > 中值, 中值 > 右值 :单调递减,不可能出现
左 中 右
分析前面三种可能的情况,会发现情况1、2是一类,情况3是另一类。
如果中值 < 右值,则最小值在左半边,可以收缩右边界。
如果中值 > 右值,则最小值在右半边,可以收缩左边界。
通过比较中值与右值,可以确定最小值的位置范围,从而决定边界收缩的方向。
而情况1与情况3都是左值 < 中值,但是最小值位置范围却不同,这说明,如果只比较左值与中值,不能确定最小值的位置范围。
所以我们需要通过比较中值与右值来确定最小值的位置范围,进而确定边界收缩的方向。
接着分析解法里的一些问题:
首先是while循环里的细节问题。
这里的循环不变式是left < right, 并且要保证左闭右开区间里面始终套住最小值。
中间位置的计算:mid = left + (right - left) / 2
这里整数除法是向下取整的地板除,mid更靠近left,
再结合while循环的条件left < right,
可以知道left <= mid,mid < right,
即在while循环内,mid始终小于right。
因此在while循环内,nums[mid]要么大于要么小于nums[right],不会等于。
这样else {right = mid;}这句判断可以改为更精确的
else if (nums[mid] < nums[right]) {right = mid;}。
再分析一下while循环退出的条件。
如果输入数组只有一个数,左右边界位置重合,left == right,不会进入while循环,直接输出。
如果输入数组多于一个数,循环到最后,会只剩两个数,nums[left] == nums[mid],以及nums[right],这里的位置left == mid == right - 1。
如果nums[left] == nums[mid] > nums[right],则左边大、右边小,
需要执行left = mid + 1,使得left == right,左右边界位置重合,循环结束,nums[left]与nums[right]都保存了最小值。
如果nums[left] == nums[mid] < nums[right],则左边小、右边大,
会执行right = mid,使得left == right,左右边界位置重合,循环结束,nums[left]、nums[mid]、nums[right]都保存了最小值。
细化了的代码:
class Solution {
public:
int findMin(vector<int>& nums) {
int left = 0;
int right = nums.size() - 1; /* 左闭右闭区间,如果用右开区间则不方便判断右值 */
while (left < right) {
/* 循环不变式,如果left == right,则循环结束 */
int mid = left + (right - left) / 2; /* 地板除,mid更靠近left */
if (nums[mid] > nums[right]) {
/* 中值 > 右值,最小值在右半边,收缩左边界 */
left = mid + 1; /* 因为中值 > 右值,中值肯定不是最小值,左边界可以跨过mid */
} else if (nums[mid] < nums[right]) {
/* 明确中值 < 右值,最小值在左半边,收缩右边界 */
right = mid; /* 因为中值 < 右值,中值也可能是最小值,右边界只能取到mid处 */
}
}
return nums[left]; /* 循环结束,left == right,最小值输出nums[left]或nums[right]均可 */
}
};
再讨论一个问题:
为什么左右不对称?为什么比较mid与right而不比较mid与left?能不能通过比较mid与left来解决问题?
左右不对称的原因是:
这是循环前升序排列的数,左边的数小,右边的数大,而且我们要找的是最小值,肯定是偏向左找,所以左右不对称了。
为什么比较mid与right而不比较mid与left?
具体原因前面已经分析过了,简单讲就是因为我们找最小值,要偏向左找,目标值右边的情况会比较简单,容易区分,所以比较mid与right而不比较mid与left。
那么能不能通过比较mid与left来解决问题?
能,转换思路,不直接找最小值,而是先找最大值,最大值偏右,可以通过比较mid与left来找到最大值,最大值向右移动一位就是最小值了(需要考虑最大值在最右边的情况,右移一位后对数组长度取余)。
以下是先找最大值的代码,可以与前面找最小值的比较:
class Solution {
public:
int findMin(vector<int>& nums) {
int left = 0;
int right = nums.size() - 1;
while (left < right) {
int mid = left + (right - left + 1) / 2; /* 先加一再除,mid更靠近右边的right */
if (nums[left] < nums[mid]) {
left = mid; /* 向右移动左边界 */
} else if (nums[left] > nums[mid]) {
right = mid - 1; /* 向左移动右边界 */
}
}
return nums[(right + 1) % nums.size()]; /* 最大值向右移动一位就是最小值了(需要考虑最大值在最右边的情况,右移一位后对数组长度取余) */
}
};
使用left < right作while循环条件可以很方便推广到数组中有重复元素的情况,即154题:
https://leetcode-cn.com/problems/find-minimum-in-rotated-sorted-array-ii/
只需要在nums[mid] == nums[right]时挪动右边界就行:
class Solution {
public:
int findMin(vector<int>& nums) {
int left = 0;
int right = nums.size() - 1;
while (left < right) {
int mid = left + (right - left) / 2;
if (nums[mid] > nums[right]) {
left = mid + 1;
} else if (nums[mid] < nums[right]) {
right = mid;
} else {
right--;
}
}
return nums[left];
}
};
初始条件是左闭右闭区间,right = nums.size() - 1,
那么能否将while循环的条件也选为左闭右闭区间left <= right?
可以的,代码如下:
class Solution {
public:
int findMin(vector<int>& nums) {
int left = 0;
int right = nums.size() - 1;
while (left <= right) {
// 循环的条件选为左闭右闭区间left <= right
int mid = left + (right - left) / 2;
if (nums[mid] >= nums[right]) {
// 注意是当中值大于等于右值时,
left = mid + 1; // 将左边界移动到中值的右边
} else {
// 当中值小于右值时
right = mid; // 将右边界移动到中值处
}
}
return nums[right]; // 最小值返回nums[right]
}
};
这道题还有其它解法:
始终将nums[mid]与最右边界的数进行比较,相当于在每次裁剪区间之后始终将最右边的数附在新数组的最右边。
class Solution {
public:
int findMin(vector<int>& nums) {
int right_boundary = nums[nums.size() - 1];
int left = 0;
int right = nums.size() - 1;
while (left < right) {
int mid = left + (right - left) / 2;
if (nums[mid] > right_boundary) {
left = mid + 1;
} else {
right = mid;
}
}
return nums[left];
}
};
或者在处理了第一种情况之后,始终将nums[mid]与最左边界的数nums[0]进行比较,即相当于在每次裁剪区间之后始终将最左边的数附在新数组的最左边,再不断处理情况2及情况3。
class Solution {
public:
int findMin(vector<int>& nums) {
int left = 0;
int right = nums.size() - 1;
if (nums[0] < nums[right])
return nums[left];
while (left < right) {
int mid = left + (right - left) / 2;
if (nums[0] > nums[mid])
right = mid;
else
left = mid + 1;
}
return nums[left];
}
};
vector<int>& nums) {
int left = 0;
int right = nums.size() - 1;
if (nums[0] < nums[right])
return nums[left];
while (left < right) {
int mid = left + (right - left) / 2;
if (nums[0] > nums[mid])
right = mid;
else
left = mid + 1;
}
return nums[left];
}
};