leetcode详细分析------236. 二叉树的最近公共祖先

题目描述：

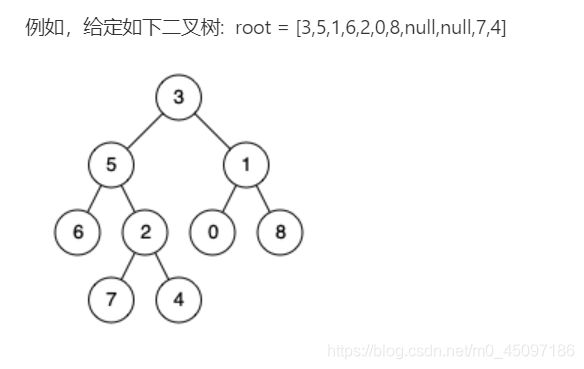
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

什么公共祖先呢？

1、比如节点6和节点2，其公共祖先是节点5
2、再比如7、4-，祖先节点是2、5、3，最近的公共祖先是2

首先我们先看两种情况：

情况①：孩子双亲表示法

• 如果二叉树是通过双亲表示法（节点中保存了双亲的位置和值域）来进行表示的，我们可以转化为两个链表求公共节点的问题。

【方法一：根据情况①】

• 代码实现：

class Solution {
     
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
     
    if(root==null || p==null || q==null){
     
        return null;
    }
    //获取p和q在root中的路径
      Stack<TreeNode> pPath = new Stack<>();//用来存放q路径
      Stack<TreeNode> qPath = new Stack<>();
      
      getPath(root,p,pPath);
      getPath(root,q,qPath);

      int pSzie = pPath.size();//q路径长度
      int qSzie = qPath.size();
      
      //1、让节点个数多的路径先出，使其最后相等
      //2、依次比较栈顶元素： 相等----公共节点
      //                    不相等----继续比较
      while(pSzie!=0 && qSzie!=0){
     
         if(pSzie>qSzie){
     
             pPath.pop();
             pSzie--;
        }else if(pSzie < qSzie){
     
             qPath.pop();
             qSzie--;
        }else if(pPath.peek()==qPath.peek()){
      //栈顶元素相同
             return pPath.peek();
        }
         else{
     
             pPath.pop();
             qPath.pop();
             pSzie--;
             qSzie--;
         }
      }
    return null;
    }
    
    //找路径的方法
    private boolean getPath(TreeNode root,TreeNode node,Stack<TreeNode> sPath){
     
        if(root == null){
     
            return false;
        }
        sPath.push(root);

        if(root == node){
     
            return true;
        }

        //递归到root的左子树 || 递归到root的右子树
        if(getPath(root.left,node,sPath) || getPath(root.right,node,sPath)){
     
            return true;
        } 
        sPath.pop();//如果不是以上三种情况，该元素出栈（该路径没有此元素）
        return false;
    }
}

情况②： 二叉搜索树

• 什么是二叉搜索树？
  
  如图所示：

• 根节点值域大于其左子树中任意节点的值域

• 根节点值域小于其右子树中任意节点的值域

• 根的左右子树都满足上述性质

  特性：

• 1、最左侧节点一定是最小的，最右侧节点一定是最大的；

• 2、进行中序遍历，可以得到一个有序序列；

【方法二-----从二叉搜索树中得到启发】

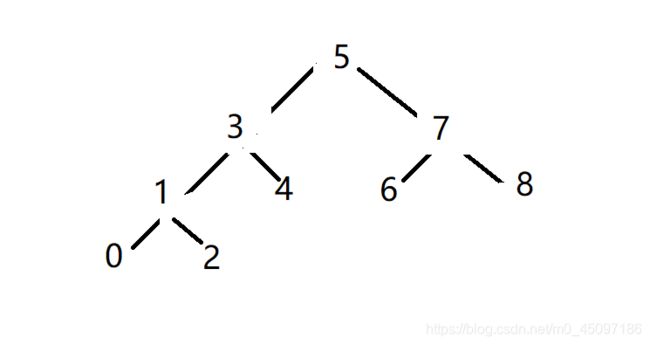
假设能知道p、q 在 root 子树中的情况：

• p、q分别在root的左右子树中，如上图中的6和0；

• p、q在root的左子树中------递归到根节点的左子树中查找

• p、q在root的右子树中------递归到根节点的右子树中查找

• 代码实现：

class Solution {
     
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
     
       
        if(root==null || q==null || p==null){
     
            return null;
        }
        //如果有一个节点在根的位置，最近公共祖先一定是根节点
        if(p==root || q==root){
     
            return root;
        }

        //检测p和q在roor子树中的情况
        boolean isPInLeft = false;
        boolean isPInRight = false;
        boolean isQInLeft = false;
        boolean isQInRight = false;

        if(isNodeInTree(root.left,p)){
      //节点p在左子树中
            isPInLeft=true;
            isPInRight=false;
        }else{
     
            isPInLeft=false;
            isPInRight=true;
        }

        if(isNodeInTree(root.left,q)){
      //节点q在左子树中
            isQInLeft=true;
            isQInRight=false;
        }else{
     
            isQInLeft=false;
            isQInRight=true;
        }

        //进行判断

        // p、q分别在root的左右子树中
        if((isPInLeft && isQInRight) || (isPInRight&&isQInLeft)){
     
            return root;
        }
        //p、q在root的左子树中------递归到根节点的左子树中查找
          else if(isPInLeft && isQInLeft){
     
            return lowestCommonAncestor(root.left,p,q);
        }
         // p、q在root的右子树中------递归到根节点的右子树中查找
         else{
     
            return lowestCommonAncestor(root.right,p,q);
         }
    } 

    //检测一个节点是否在二叉树中
    private boolean isNodeInTree(TreeNode root,TreeNode node){
     
        if(root==null){
     
            return false;
        }
        if(root==node){
     
            return true;
        }
        if(isNodeInTree(root.left,node)||isNodeInTree(root.right,node)){
     
            return true;
        }
        return false;
    }
}