Kmeans聚类介绍及R语言实现
K-means介绍
k-means算法简介:
K-means算法是IEEE 2006年ICDM评选出的数据挖掘的十大算法中排名第二的算法,排名仅次于C4.5算法。K-means算法的思想很简单,简单来讲就是对于给定的样本集,按照样本之间的距离大小,将样本集划分为K个簇。让簇内的点尽量紧密的连在一起,而让簇间的距离尽量的大,两个对象之间的距离越近,相似性越高。聚类的结果就是使类内部的同质性高,而类之间的异质性高。
k-means算法的具体工作流程如下:
step1:导入一组具有n个对象的数据集,给出聚类个数k;
step2:从n个对象中随机取出k个作为初始聚类中心;
step3:根据欧几里得距离来判断相似度量,确定每个对象数据哪个簇;
step4:计算并更新每个簇中对象的平均值,并将其定为每个簇的新的聚类中心;
step5:计算出准则函数E;
step6:循环step3,step4,step5直到准则函数E在允许的误差范围内;
k-means算法的几个主要特点:
- 发现球形互斥的簇:由于K-means算法一般是以欧几里得距离作为相似性度量指标,所以K-means算法对于球形互斥的簇的聚类效果会比较好;
- 对低维数据集效果较好:同样的数据量,维度越高,数据矩阵越稀疏,当数据维度比较高时,数据矩阵是一个稀疏矩阵,K-means算法稀疏矩阵数据聚类效果不佳;
- 容易陷入局部最优:对于K-means算法来说,初始聚类中心的确定十分重要,因为不同的聚类中心会使算法沿着不同的路径搜索最优聚类结果,不过对于陷入局部最优这个问题可以从初始聚类中心的选择来进行改进。
R语言编程实现:
##### 案例数据 #########
setwd("E:/data")
data_model <- read.csv("data.csv",header = T)
data_model_1 <- data_model[,1:4]
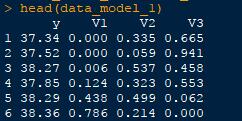
head(data_model_1)
######## 数据查看 ###############
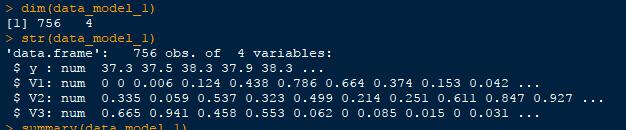
dim(data_model_1)
str(data_model_1)
summary(data_model_1)
# y~V1-Vn数据相关性探索
(data_cor <- cor(data_model_1))
library(car)
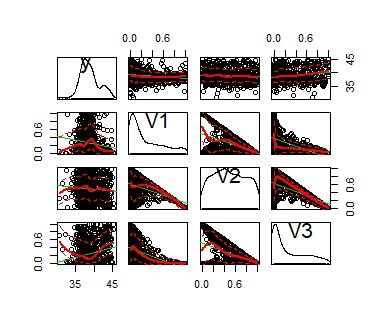
scatterplotMatrix(data_model_1)
相关关系不是特别明显,进行量化表现:
library(corrplot)
corrplot(corr = data_cor, method = 'color', addCoef.col="grey")
可以明显看出y和V1、V2呈负相关关系,系数分别为-0.15及-0.07,y和V3呈正相关关系,且系数较高为0.22。
K-means模型训练
data <- data_model_1[,2:4]
定义kmeans聚类函数My_Kmeans
#默认的最大迭代次数为10
My_kmeans <- function(data,k,max.iter=10){
rows <- nrow(data)
cols <- ncol(data)
within <- matrix(0,nrow=k,ncol=1)
between <- 0
iter = 0
#定义indexMatrix矩阵,第一列为每个数据所在的类,第二列为每个数据到其类中心的距离
indexMatrix <- matrix(0,nrow=rows,ncol=2)
centers <- matrix(0,nrow=k,ncol=cols)
randSeveralInteger <- as.vector(sample(1:rows,size=k))
#通过生成随机数的方式,得到初始的聚类中心
for(i in 1:k){
indexMatrix[randSeveralInteger[i],1] <- i
centers[i,] <- data[randSeveralInteger[i],]
centers <- matrix(centers,k,cols)
}
changed = TRUE
while(changed){
if(iter >= max.iter)
break
changed=FALSE
#对每一个数据,计算其到各个类中心的距离,并将其划分到距离最近的类
for(i in 1:rows){
initialDistance <- 10000
previousCluster <- indexMatrix[i,1]
#遍历所有的类,将该数据划分到距离最近的类
for(j in 1:k){
currentDistance <- (sum((data[i,]-centers[j,])^2))^0.5
if(currentDistance < initialDistance){
initialDistance <- currentDistance
indexMatrix[i,1] <- j
indexMatrix[i,2] <- currentDistance
}
}
#如果该数据所属的类发生了变化,则将changed设为TRUE,算法继续
if(previousCluster!=indexMatrix[i,1])
changed=TRUE
}
#重新计算类中心
for(m in 1:k){
clusterMatrix <- data[indexMatrix[,1]==m,]
clusterMatrix <- as.matrix(clusterMatrix)
if(nrow(clusterMatrix)>0){
centers[m,] <- colMeans(clusterMatrix)
}
else{
centers[m,] <- centers[m,]
}
}
iter = (iter+1)
}
参数注释:
- data:表示待聚类的数据
- k:要聚类的数目
- max.iter:聚类的最大迭代次数,默认值是10
- cluster:聚类的结果,也就是每个对象所属的类
- tot.withinss:聚类的总的类内平方和,用来衡量类内差异
- betweenss:聚类的类间平方和,用来衡量类间差异
原始数据标准化
min.max.norm <- function(x){
((x-min(x))/(max(x)-min(x)))
}
data <- apply(data,2,min.max.norm)
确定最优K
# k取2到8,评估K
library(fpc)
K <- 2:8
round <- 10 # 每次迭代10次,避免局部最优
rst <- sapply(K, function(i){
print(paste("K=",i))
mean(sapply(1:round,function(r){
print(paste("Round",r))
result <- My_kmeans(data, i)
stats <- cluster.stats(dist(data), result$cluster)
stats$avg.silwidth
}))
})
# 可以看到如下的示意图
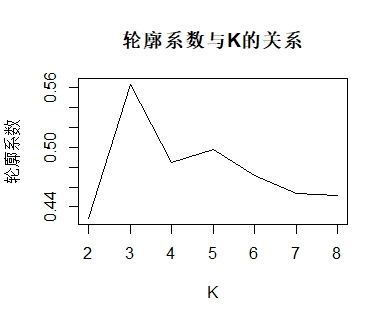
plot(K,rst,type='l',main='轮廓系数与K的关系', ylab='轮廓系数') #轮廓系数越大越好
可以看出,当K=3时,轮廓系数最大,因此我们取K=3。
实际数据检验函数
result <- My_kmeans(data,k=3) #进行聚类
result$cluster
result$tot.withinss
result$betweenss
result$iteration
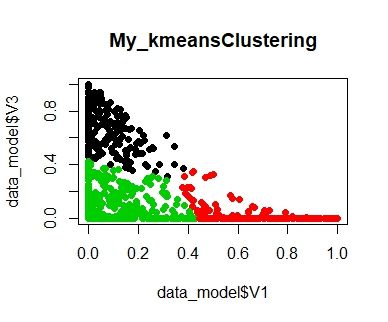
聚类结果可视化
plot(data_model$V1,data_model$V3,col=result$cluster,main="My_kmeansClustering",pch=19)
聚类结果导出
result_output <- data.frame(data_model[,1:4],result$cluster)
write.csv(result_output,file="result_output.csv",row.names=T,quote=F)
三个分群的概率密度函数图
Data1 <- data_model[,2:4][which(result_output$result.cluster==1),]
Data2 <- data_model[,2:4][which(result_output$result.cluster==2),]
Data3 <- data_model[,2:4][which(result_output$result.cluster==3),]
opar <- par(no.readonly = TRUE) #复制一份单签的图形参数
png("kmean.png")
par(mfrow = c(3,3))
plot(density(Data1[,1]),col="red",main="R")
plot(density(Data1[,2]),col="red",main="F")
plot(density(Data1[,3]),col="red",main="M")
plot(density(Data2[,1]),col="red",main="R")
plot(density(Data2[,2]),col="red",main="F")
plot(density(Data2[,3]),col="red",main="M")
plot(density(Data3[,1]),col="red",main="R")
plot(density(Data3[,2]),col="red",main="F")
plot(density(Data3[,3]),col="red",main="M")
par(opar)