实现一个简单的谢林模型(Schelling Model)
by tjuarch
1 简介
谢林模型,也叫谢林隔离模型,是由美国经济学家托马斯·谢林于1971年提出,描述同质性在空间隔离上的影响和作用。
它是基于智能体的模型,包含有三个元素:
1、会产生行为的智能体
2、智能体行为遵循一定的规则
3、智能体产生的行为会导致宏观上的结果
2 python实现
模型揭示的一些事实在实际中得到了验证,人们对于身边各种不同阶层邻居的存在,但是最终经过有限次的迁徙后,却形成了隔离。
采用python语言,在matplotlib中进行画图,用numpy计算矩阵。
主要流程包括几个步骤:
1、初始化网格,50x50的点阵,用三种颜色表示,包括两个分类和一个空白格子。设定满意度阈值、画布大小以及三类格子的生成比例(40%,40%,20%)。
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
# np.random.seed(198108)
N = 50
threshold = 0.7
figsize=(12,12)
x = np.arange(N)
y = np.arange(N)
X, Y = np.meshgrid(x, y)
# Z = np.random.rand(N, N)
status = ["C1", "C4", 'white']
prob = [0.4, 0.4, 0.2]
def init_z():
Z = np.random.choice(a=status, size=(N**2), p=prob)
Z.shape = (N, N)
return Z
Z = init_z()
2、计算每个点的满意程度get_cell_happiness(),也即周边同种类格子的比例,得到一个满意度矩阵get_all_happiness()。
3、计算所有格子的平均满意度(hap_mean)、不满意格子的比例(unhap_ratio),计算阈值下不满意格子的位置get_unhap_cells()。
4、随机选择一个不满意的格子搬家。但是要注意搬走之后形成新的空位以及及时刷新空格的位置列表。
5、重新计算满意程度,进行新一轮的搬家行动,最终计算经过多少步能达到目的,及不满意格子的比例达到一个比较低的水平。
def get_null_cells(Z):
"""获取空白格子的位置
Z:np.array, N*N
return:list of cells position
"""
if not Z.shape == (N, N):
Z.shape = (N, N)
cells = np.where(Z == "white")
return cells
def get_cell_happiness(Z, row, col):
"""获取每个单元格的满意程度阈值
Z: N*N np.array
row: int, col:int
return: happiness:int
"""
if not Z.shape == (N, N):
Z.shape = (N, N)
if Z[row, col] == "white":
return np.NaN
same, count = 0, 0
left = 0 if col==0 else col-1
right = Z.shape[1] if col==Z.shape[1]-1 else col+2
top = 0 if row==0 else row-1
bottom = Z.shape[0] if row==Z.shape[0]-1 else row+2
# print(top, bottom, left, right)
for i in range(top, bottom):
for j in range(left, right):
# print(list(range(left, right)))
if (i, j) == (row, col) or Z[i,j] == "white":
continue
# print(Z[i,j], i, j)
elif Z[i, j] == Z[row, col]:
same += 1
count += 1
else:
count += 1
# print('in',same,count)
if not count == 0:
happiness = same / count
else:
happiness = 0
return happiness
def get_all_happiness(Z):
"""得到所有格子的满意度
return: np.array N*N
"""
hap_scores = []
for row in range(Z.shape[0]):
for col in range(Z.shape[1]):
# print(row, col)
hap_scores.append(get_cell_happiness(Z, row, col))
hap_scores = np.array(hap_scores)
hap_scores.shape = Z.shape
return hap_scores
def hap_mean(Z):
"""所有格子的平均满意度
return: res -> int
"""
hap_scores = get_all_happiness(Z)
res = hap_scores[np.where(hap_scores>=0)].mean()
return res
def get_unhap_cells(Z=Z, threshold=threshold):
"""得到不满意的格子
return: tuple 2 items
"""
hap_scores = get_all_happiness(Z)
res = np.where(hap_scores < threshold)
return res
def unhap_ratio(Z):
hap_scores = get_all_happiness(Z)
res = np.sum(hap_scores<threshold) / np.sum(hap_scores>=0)
# unhap_count = len(get_unhap_cells()[0])
# print(unhap_count)
# res = unhap_count / len(Z[np.where(Z!="white")])
return res
def move(Z):
unhap_cells = get_unhap_cells()
for i in range(len(unhap_cells[0])):
blank_cells = get_null_cells(Z)
unhap_row = unhap_cells[0][i]
unhap_col = unhap_cells[1][i]
j = np.random.choice(range(len(blank_cells[0])))
blank_row = blank_cells[0][j]
blank_col = blank_cells[1][j]
Z[unhap_row, unhap_col], Z[blank_row, blank_row] = Z[blank_row, blank_row], Z[unhap_row, unhap_col]
6、用matplotlib画图,定义了几个画图函数:
draw_raw():画出现有的点矩阵情况
draw_nullcells():画出空格,并随机选一个空格
draw_happiness():全局的满意度得分
draw_unhapcells():全局的不满意格子分布
find_times_equal():计算达到均衡需要的搬家次数并绘图
3 简单分析
1、生成50 * 50 点阵,参数如图
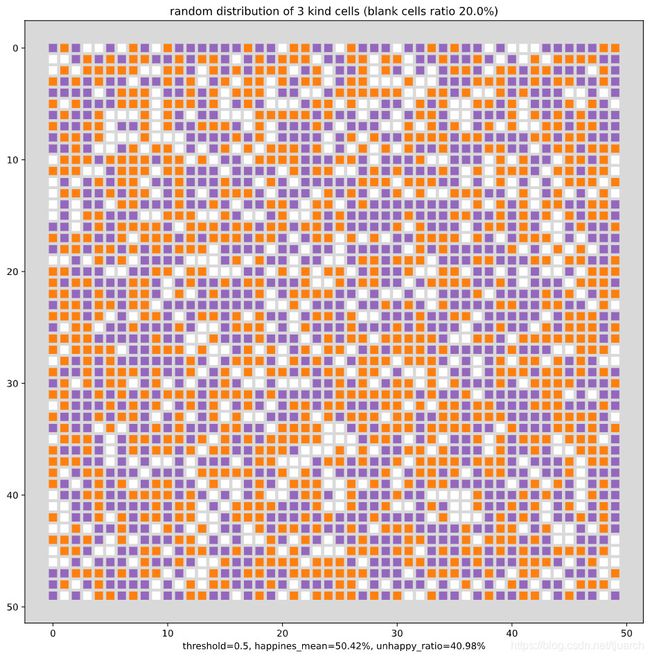
这是一个平均满意度50.42%, 不满意率40.98%的模拟2500人的矩阵。
2、各种参数
空白格子以及随机的一个空格

全局满意度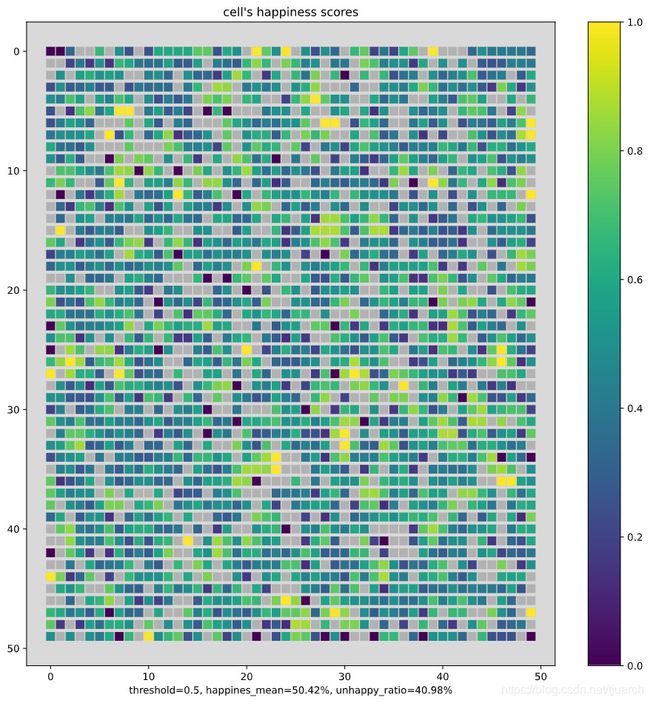
不满意格子的分布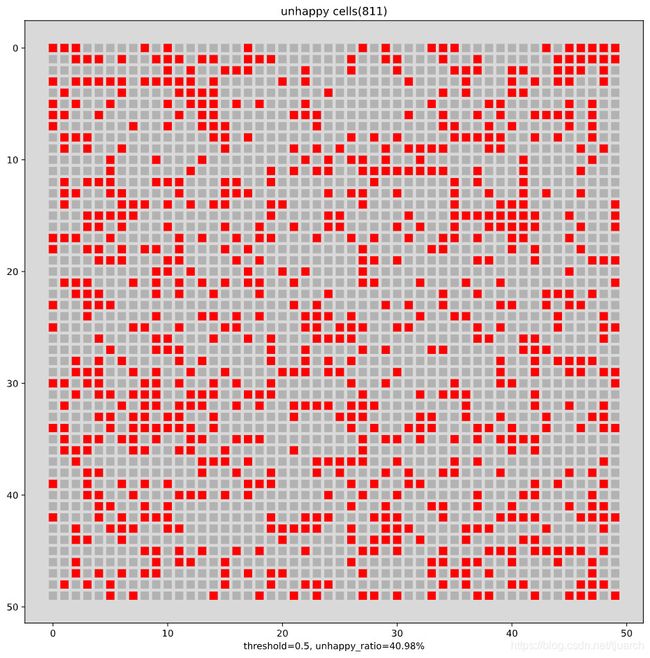
迁移5次以后的分布情况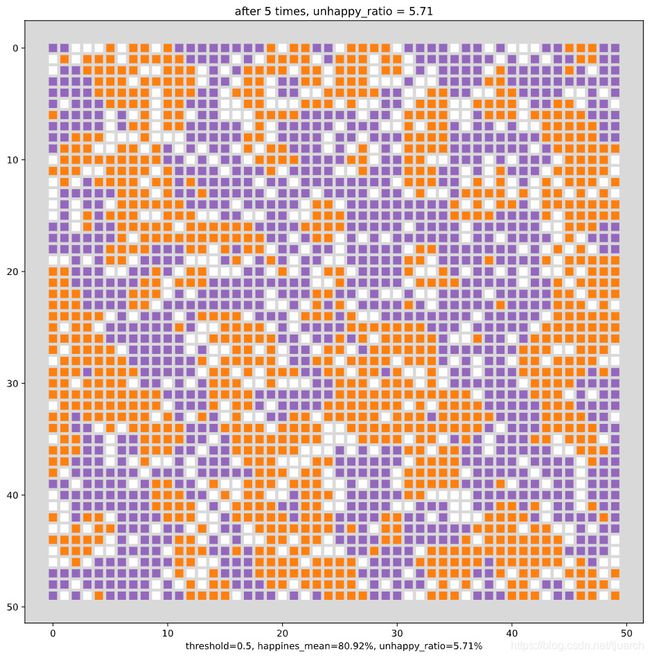
最终经过21轮迁移,不满意度降低到1%

整体满意得分88.25
4源码
源码在此,欢迎下载,祝大家玩得愉快!
https://github.com/tjuarch/schelling_model/blob/main/my_schelling_model3.ipynb