Pytorch学习笔记 2.2：线性回归下的梯度下降

线性回归下的梯度下降

The Gradient Descent Of Linear Regression

自学视频PyTorch学这个就够了！：
课件以及代码：Pytorch.zip
这节课(lesson 3)用到的数据集和代码：lesson03代码及数据.zip
我用的Pycharm运行的，大家关注我就能下载了，不用收费 呜呜呜。

学他学他学他！就学他！讲的太透彻了，我刚上初中就能听明白，小白一枚之前看Pytorch的教程死活看不懂，没想到这个一看就明白了！兄弟姐妹们学起来！

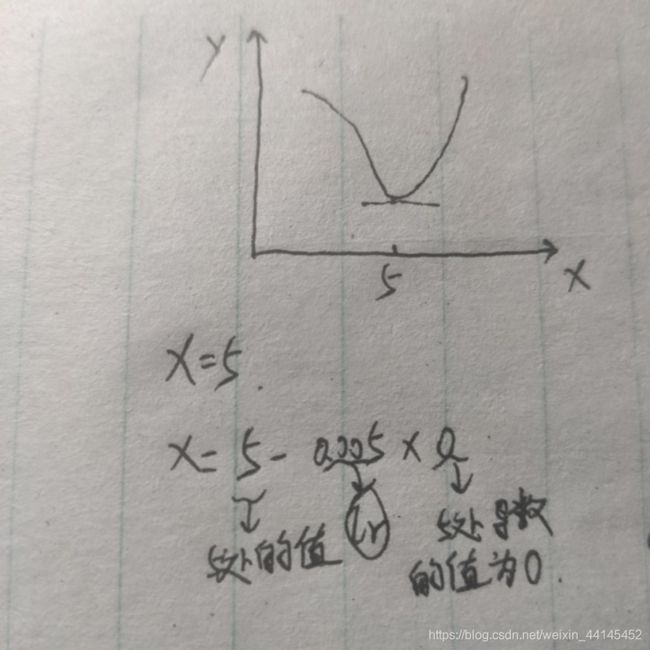
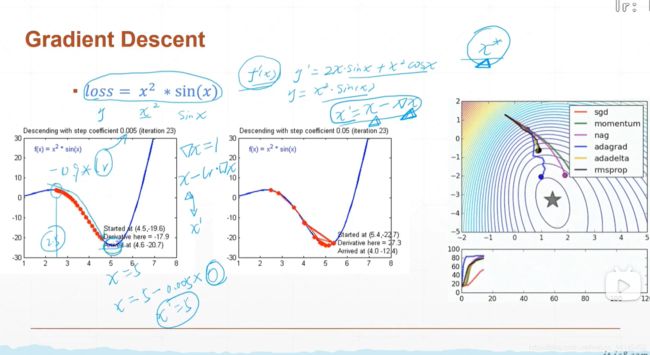这里有一个loss函数：
当loss值最低的时候，就是求得的结果与预期结果最接近的时候。

文字描述不完 就直接上图了

代码：

import matplotlib.pyplot as plt
from matplotlib import pyplot as plt
import numpy as np
import torch
import pandas as pd

# %matplotlib inline
# %config InlineBackend.figure_format = 'svg'
# 绘制 loss 曲线
train_loss_results = []  # 将每轮的loss记录在此列表中，为后续画loss曲线提供数据


points = np.genfromtxt('l3_data.csv',delimiter = ',')
plt.scatter(points[:,0],points[:,1],c = '',edgecolors = 'b',s = 15)
plt.show()

# y = wx + b
def compute_error_for_line_given_points(b, w, points):
    """
        计算给定超参数[w,b]的误差值
    """
    totalError = 0
    for i in range(0, len(points)):
        x = points[i, 0]
        y = points[i, 1]
        totalError += (y - (w * x + b)) ** 2
    return totalError / float(len(points))


def step_gradient(b, w, points, lr):
    b_gradient = 0
    w_gradient = 0
    N = float(len(points))
    for i in range(len(points)):
        x = points[i, 0]
        y = points[i, 1]
        b_gradient += -(2/N) * (y - ((w * x) + b))
        w_gradient += -(2/N) * x * (y - ((w * x) + b))
    b_new = b - (lr * b_gradient)
    w_new = w - (lr * w_gradient)

    return [b_new, w_new]


def gradient_descent_runner(points, b, w, lr, iterations):
    """
        梯度下降
    """
    for i in range(iterations):
        b, w = step_gradient(b, w, np.array(points), lr)
        print("iterations {}, loss: {}".format(i, compute_error_for_line_given_points(b,w,points)))
        train_loss_results.append(compute_error_for_line_given_points(b,w,points))  # 将4个step的loss求平均记录在此变量中
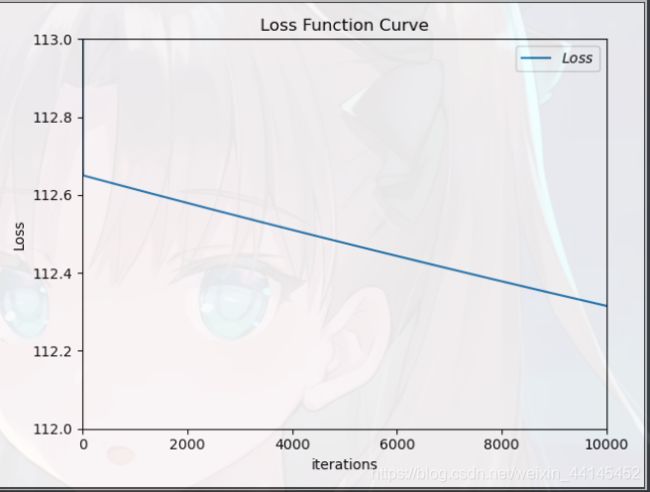
    plt.title('Loss Function Curve')  # 图片标题
    plt.xlabel('iterations')  # x轴变量名称
    plt.ylabel('Loss')  # y轴变量名称
    plt.axis([0, 10000, 112, 113])
    plt.plot(train_loss_results, label="$Loss$")  # 逐点画出trian_loss_results值并连线，连线图标是Loss
    plt.legend()  # 画出曲线图标
    plt.show()  # 画出图像
    return [b, w]

def run():
    points = np.genfromtxt('l3_data.csv', delimiter = ',')
    lr = 0.0001
    initial_b = 0
    initial_w = 0
    iterations = 10000
    print(f"Starting project descent at b = {initial_b}, w = {initial_w}, error = {compute_error_for_line_given_points(initial_b,initial_w,points)}")
    print('\nRunning...')
    [b, w] = gradient_descent_runner(points, initial_b, initial_w, lr, iterations)
    print(f"\nAfter project descent at b = {b}, w = {w},error = {compute_error_for_line_given_points(b,w,points)}")
    print('\nb:{}，w:{}'.format(b, w))


if __name__ == '__main__':
    run()
   

里面用了三个函数：
第一个函数：compute_error_for_line_given_points(b, w, points):是用来就是来计算loss均值的
第二个函数：step_gradient(b, w, points, lr): 计算 b 和 w的梯度值
第三个函数：gradient_descent_runner(points, b, w, lr, iterations):运行10000次，不断迭代b和w，批量梯度下降，优化参数
运行结果：


x-y散点图

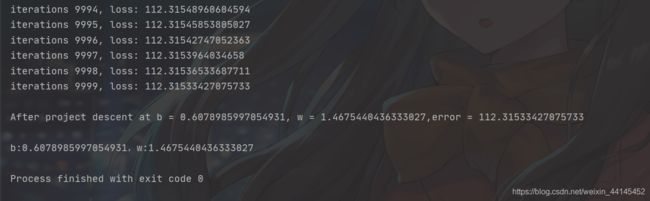
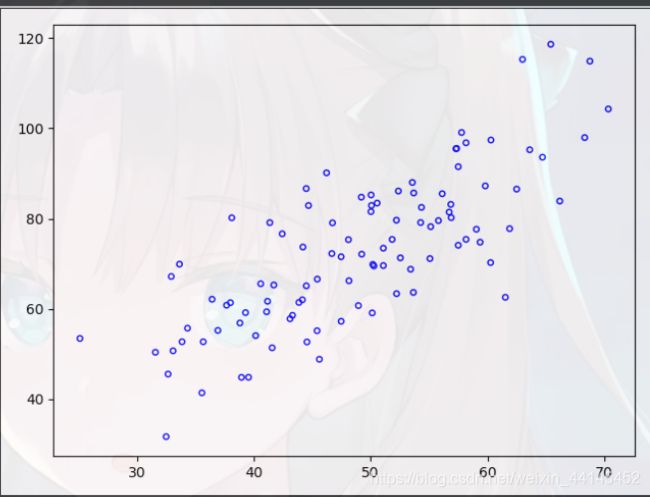
loss随迭代次数下降图