Pytorch 入门学习笔记+深度学习代码示例

---

1.0 Pytorch是什么

Pytorch是一种基于Python的科学计算软件包，面向两组受众：

1.替代NumPy以使用GPU的功能
2.提供最大灵活性和速度的深度学习研究平台

---

2.0 Pytorch 的安装

2.1 Pytorch 的安装方式

首先电脑需要装有Anoconda或者MINIconda

1.推荐使用Pytorch清华镜像相对下载速度很快，一定要根据链接教程通过修改用户目录下的 .condarc 文件。Windows 用户无法直接创建名为 .condarc 的文件，可先执行 conda config --set show_channel_urls yes 生成该文件之后再修改。

2.Pytorch官网下载根据自己的机型选择下载方式（下载速度非常慢）

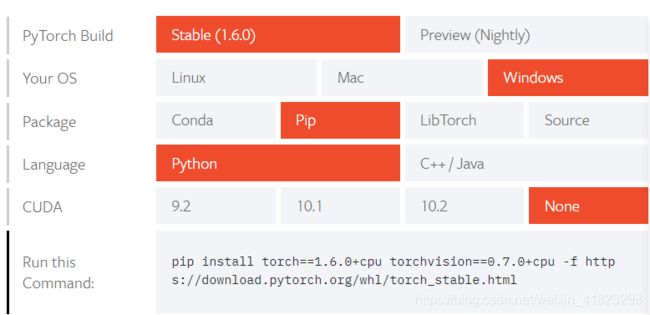
2.2 Pytorch 的安装结果

安装完成之后可以在conda中使用：

(base)<users>python
>>import torch
>>torch .__versin__

来检查是否安装成功

---

3.0 Pytorch 入门编程

3.1 Pytorch 中Tensors的使用

Tensors与NumPy的ndarray相似，此外，Tensor也可以在GPU上使用以加速计算。

>>from __future__ import print_function
>>import torch

---

3.1.1 首先是tensor的创建：

x = torch.zeros(5, 3, dtype=torch.long)
print(x)

运行可以得到

tensor([[0, 0, 0],
        [0, 0, 0],
        [0, 0, 0],
        [0, 0, 0],
        [0, 0, 0]])

3.1.2如果想知道一个tensor的size:

print(x.size())

输出结果：

torch.Size([5, 3])

我们可以看到这是一个5*3的矩阵.

3.1.3简单的tensor的运算:
创建一个空的tensor并用以保留两个tensor相加的结果输出

result = torch.empty(5, 3)
torch.add(x, y, out=result)

3.2 Pytorch 中tensor与numpy的转换以及将tensor转入CUDA

3.2.1将numpy数组转换为torch 中的tensor:

可以通过 torch.from_numpy() 来实现数据的转换：

import numpy as np
a = np.ones(5)
b = torch.from_numpy(a)
np.add(a, 1, out=a)
print(a)
print(b)

输出结果：

[2. 2. 2. 2. 2.]
tensor([2., 2., 2., 2., 2.], dtype=torch.float64)

3.2.2将numpy数组转换为torch 中的tensor:
可以通过 .to 来实现数据的转换,从而将tensor转入任何设备中（一般进行网络训练都会转入cuda进行加速）：

# let us run this cell only if CUDA is available
# We will use ``torch.device`` objects to move tensors in and out of GPU
if torch.cuda.is_available():
    device = torch.device("cuda")          #  CUDA 
    y = torch.ones_like(x, device=device)  # directly create a tensor on GPU
    x = x.to(device)                       # or just use strings ``.to("cuda")``
    z = x + y
    print(z)
    print(z.to("cpu", torch.double))       # ``.to`` can also change dtype together!

输出结果：

tensor([0.0043], device='cuda:0')
tensor([0.0043], dtype=torch.float64)

3.3 Pytorch 的自动分类

---

---

PyTorch中所有神经网络的核心是autograd软件包。 让我们先简要地介绍一下，然后再训练第一个神经网络。

autograd软件包为Tensor上的所有操作提供自动区分。 这是一个按运行定义的框架，这意味着backprop是由代码的运行方式定义的，并且每次迭代都可以不同。

让我们用一些示例更简单地说明这一点。

---

---

3.3.1 Tensors:

Torch.Tensor是程序包的中心类。如果将其属性.requires_grad设置为True，它将开始跟踪对其的所有操作。完成计算后，可以调用.backward（）并自动计算所有渐变。该张量的梯度将累积到.grad属性中。要停止Tensor跟踪历史记录，可以调用.detach（）将其与计算历史记录分离，并防止跟踪将来的计算。

为了防止跟踪历史记录（和使用内存），还可以使用torch.no_grad（）：包装代码块。这在评估模型时特别有用，因为模型可能具有可训练的参数，且require_grad = True，但我们不需要梯度。

还有另外一类对自动实施非常重要的类- Function。

Tensor和函数相互连接并建立一个非循环图，该图对完整的计算历史进行编码。每个张量都有一个.grad_fn属性，该属性引用创建了张量的函数（用户创建的张量除外-它们的grad_fn为None）。

如果要计算导数，可以在Tensor上调用.backward（）。如果tensor是标量（即，它包含一个元素数据），则无需为后面的（）内指定任何参数，但是，如果Tensor具有更多元素，则需要指定一个渐变形状的 tensor作为梯度参数。

3.3.2 pytorch自动分类的具体应用（Tensors）:
创建一个tensor并设置require_grad = True来跟踪它的计算:

x = torch.ones(2, 2, requires_grad=True)
print(x)

输出结果：

tensor([[1., 1.],
        [1., 1.]], requires_grad=True)

---

此时对tensor进行一次运算:

y = x + 2
print(y)

输出结果：

tensor([[3., 3.],
        [3., 3.]], grad_fn=)

---

y是作为一个结果而被创建的，因此具有grad_fn：

print(y.grad_fn)

输出结果：

---

现在对y进行更多的操作：

z = y * y * 3
out = z.mean()

print(z, out)

输出结果：

tensor([[27., 27.],
        [27., 27.]], grad_fn=) tensor(27., grad_fn=)

---

.requires_grad_（）会更改现有Tensor的require_grad。 如果未给出输入，则默认为False：

a = torch.randn(2, 2)
a = ((a * 3) / (a - 1))
print(a.requires_grad)
a.requires_grad_(True)
print(a.requires_grad)
b = (a * a).sum()
print(b.grad_fn)

输出结果：

False
True

---

3.3.3 pytorch自动分类的具体应用（Gradients）:

现在开始反向传播。 因为out只包含单个标量，所以out.backward()等同于out.backward(torch.tensor(1.))

打印渐变d(out)/dx

out.backward()
print(x.grad)

输出结果：

tensor([[4.5000, 4.5000],
        [4.5000, 4.5000]])

---

现在，让我们看一个雅可比向量的示例：

x = torch.randn(3, requires_grad=True)

y = x * 2
while y.data.norm() < 1000:
    y = y * 2

print(y)

输出结果：

tensor([ 921.4462, -305.1625, -704.4802], grad_fn=)

---

现在，在这种情况下，y不再是标量. torch.autograd无法直接计算完整的雅可比行列式，但是如果我们只想要雅可比乘积，只需将向量作为参数传递给backward即可：

v = torch.tensor([0.1, 1.0, 0.0001], dtype=torch.float)
y.backward(v)

print(x.grad)

输出结果：

tensor([5.1200e+01, 5.1200e+02, 5.1200e-02])

---

也可以通过使用torch.no_grad()将代码块包装在.requires_grad = True中，从而停止自动张量跟踪在Tensor上的历史记录：

print(x.requires_grad)
print((x ** 2).requires_grad)

with torch.no_grad():
    print((x ** 2).requires_grad)

输出结果：

True
True
False

---

或者使用.detach()获得具有相同内容但不需要渐变的新Tensor：

print(x.requires_grad)
y = x.detach()
print(y.requires_grad)
print(x.eq(y).all())

输出结果：

True
False
tensor(True)

4.0 Pytorch 示例卷积神经网络代码

4.1 卷积神经网络的构建

可以使用torch.nn包构建神经网络。

现在我们已经了解了autograd，nn依靠autograd定义模型并对其进行区分。 nn.Module包含图层以及返回输出的方法forward（input）。

现在我们对下面这个数字图像进行分类的卷积神经网络进行分析：

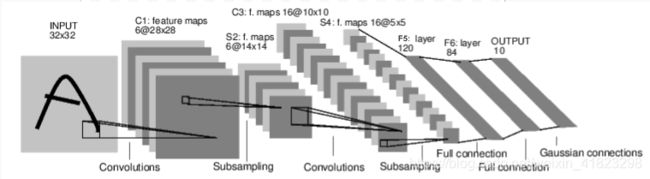
这是一个简单的前馈网络。 它获取输入，将其一层又一层地馈入，然后最终给出输出。

神经网络的典型训练过程如下：

1. 定义具有一些可学习参数（或权重）的神经网络
2. 遍历输入数据集
3. 通过网络处理输入
4. 计算损失（输出正确的距离有多远）
5. 将渐变传播回网络参数
6. 通常使用简单的更新规则来更新网络的权重：weight = weight - learning_rate * gradient

现在我们来定义这个卷积神经网络：

import torch
import torch.nn as nn
import torch.nn.functional as F


class Net(nn.Module):

    def __init__(self):
        super(Net, self).__init__()
        # 1 input image channel, 6 output channels, 3x3 square convolution
        # kernel
        self.conv1 = nn.Conv2d(1, 6, 3)
        self.conv2 = nn.Conv2d(6, 16, 3)
        # an affine operation: y = Wx + b
        self.fc1 = nn.Linear(16 * 6 * 6, 120)  # 6*6 from image dimension
        self.fc2 = nn.Linear(120, 84)
        self.fc3 = nn.Linear(84, 10)

    def forward(self, x):
        # Max pooling over a (2, 2) window
        x = F.max_pool2d(F.relu(self.conv1(x)), (2, 2))
        # If the size is a square you can only specify a single number
        x = F.max_pool2d(F.relu(self.conv2(x)), 2)
        x = x.view(-1, self.num_flat_features(x))
        x = F.relu(self.fc1(x))
        x = F.relu(self.fc2(x))
        x = self.fc3(x)
        return x

    def num_flat_features(self, x):
        size = x.size()[1:]  
        num_features = 1
        for s in size:
            num_features *= s
        return num_features


net = Net()

可以看到，在pytorch中，我们只需要定义forward函数，就可以使用autograd自动定义backward函数（计算梯度）。同样，我们也可以在forward函数中使用任何Tensor操作。

定义完网络之后可以使用net.parameters()返回模型的可学习参数

---

4.1 LOSS 函数的构建

损失函数采用一对(output, target)输入，并计算一个值，该值估计输出与目标的距离。

nn函数包下有几种不同的损失函数。 一个简单的损失是：nn.MSELoss，它计算输入和目标之间的均方误差。

例如：

output = net(input)
target = torch.randn(10)  # a dummy target, for example
target = target.view(1, -1)  # make it the same shape as output
criterion = nn.MSELoss()

loss = criterion(output, target)

5.0 Pytorch 的网络训练实操

总之，pytorch相对而言非常适用于网络模型的构建训练，后续我会放出对于自己手码的RNN 对于MINST数据集的代码 以及Resnet 对于CIFAR10数据集的代码详情看我后续更的文章。

更新：
Pytorch实现Resnet训练CIFAR10数据集（完整代码，可进一步优化）