吴恩达机器学习(无监督学习)
(1)无监督学习
这一章中将介绍无监督学习中的聚类算法,那么什么是无监督学习呢?
首先,拿监督学习来进行比较,这是一个典型的监督学习的例子,有一个带标签的训练集,目标是找到一条能够区分正样本和负样本的决策边界,如下图:

这里的监督学习问题是指有一系列标签,用假设函数去拟合它。
而相比于无监督学习中,数据并不带有任何标签,得到的数据如下图:

因此在无监督学习中,要将这系列无标签的数据输入到算法中,然后让算法找到一些隐含在数据中的结构,上图中能找到的结构就是两组分开的点集,而这些能找出这些点集的算法被称为聚类算法。记住,聚类算法clutering只是无监督学习的一种,不是所有的无监督学习都是聚类算法
(2)K-Means算法
在聚类问题中,会给定一组未加标签的数据集,希望有一个算法能够自动地将这些数据分成有紧密关系的子集或簇。K-Means算法现在是最火热也是最为广泛应用的聚类算法,本节中将介绍K-Means算法的定义及原理。
假设有一个无标签数据集如下图所示:

现在想将其分为两个簇,使用K-Means算法来进行操作,操作步骤:
(1)首先随机生成两个点,这两点叫做聚类中心。K-Means算法是一个迭代算法,它会做两件事,第一个是簇分配,第二个是移动聚类中心。

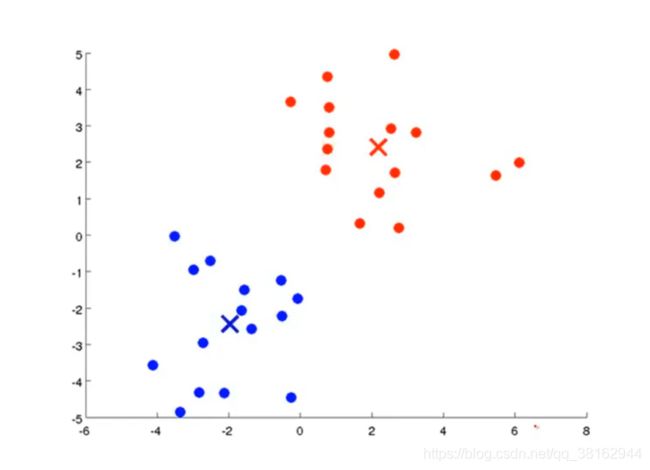
(2) 簇分配:K-Means算法中每次内循环的第一步要进行簇分配,也就是说,遍历每个样本点,根据每个样本与红色聚类中心更近还是蓝色中心更近来将每个样本点分配个两个聚类中心之一。具体的说,就是讲靠近蓝色聚类中心的点染成蓝色,靠近红色聚类中心的点染成红色。

(3) 移动聚类中心:K-Means算法中每次内循环的第二步要移动聚类中心,要做是找到所有蓝点并计算出它们的均值,然后把蓝色聚类中心移到那里,红色聚类中心也是一样的操作。

(4)然后接着继续做簇分配和移动聚类中心,迭代多次之后,就会完成最终的两个点集的聚类,这就可以说K-Means算法已经聚合了。
下面用更规范的格式写出K-Means算法:


这里还要介绍K-Means算法另一个常见的应用:它可以用来解决分离不佳的簇的问题,具体地说,目前为止,K-Means算法都基于像下图中这样的数据集,它们很明显是可以分成3个簇的数据。

但在实际中,K-Means算法也会用于下图中这样的数据集,看起并不能很好地分成几个簇。

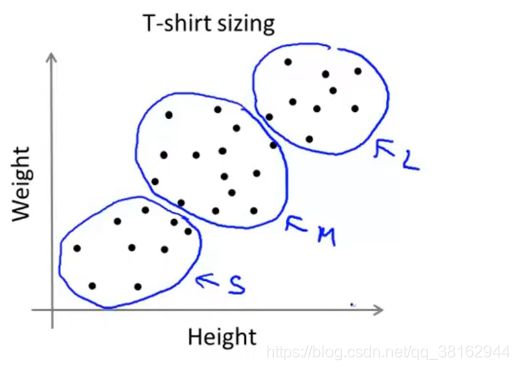
实际例子中,要根据顾客的身高体重来设计T-恤的尺寸,小号、中号、大号,那么尺码又该设计多大?有一个方法就是对上图中的数据集执行K-Means算法,算法可能会将数据分成下图中的3个簇。所以尽管数据集不是很明显的能分成3个簇,K-Means算法还是能将这些数据分为3个簇,这类似于市场细分的案例。
(3)优化目标
类似于之前提到的线性回归等算法,K-Means算法也有一个优化目标函数或者用于最小化的代价函数,这一节中将探讨这个优化目标函数是什么。
执行K-Means算法时,将会对3组变量进行跟踪。

有了上述所说变量,下面给出K-Means算法的优化目标:
这个代价函数有时也叫失真代价函数或者K-Means算法的失真。
在K-Means算法中的第一步簇分配的步骤中,其实就是在最小化代价函数J,
第二步移动聚类中心的步骤中,其实就是选择μ值来最小化代价函数J。
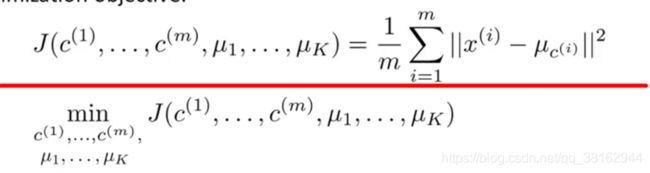
(4)随机初始化
这一节中将讨论如何初始化K-Means算法,更重要的是探讨如何使算法避开局部最优。
这是之前介绍过的K-Means算法:

那么如何初始化聚类中心,这里有几种不同的方法可以用来随机初始化聚类中心。通常用下面的这种方法:
当运行K-Means算法时:
(1)应该把聚类中心的数值K设置为比训练样本数量m小的值;
(2)随机挑选K个训练样本;作为初始聚类中心
(3)设定μ1,…,μk,让它们等于这K个样本。
K-Means算法中的局部最优问题:
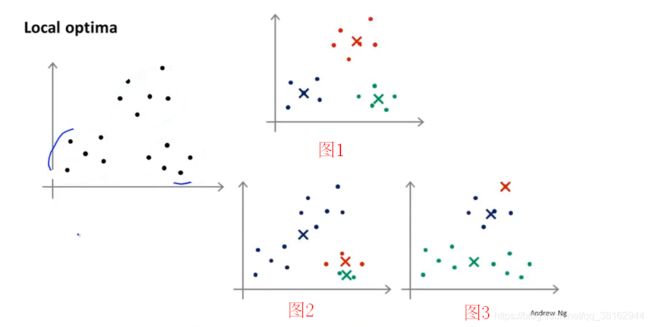
K-Means算法最终可能会落在局部最优,给定以下的数据集,执行算法,最终可能得到一个比较好的局部最优,实际是全局最优。如图1所示
但是如果随机初始化,得到的结果不好的话,就可能会得到不同的局部最优值,如下图2、3所示。
实际上,上述图3中的红色聚类只捕捉到了一个无标签的样本,而局部最优这个术语指的是代价函数J的局部最优。
因此,如果想让找到最优可能的聚类,可以尝试多次随机初始化,以此来保证能够得到一个足够好的结果,下面是多次随机初始化的具体做法:
在所有的100种分类数据的方法中选取代价最小的一个也就是代价函数J最小的。事实证明,在聚类数K较小的情况下(2~10个),使用多次随机初始化会有较大的影响,而如果K很大的情况,多次随机初始化可能并不会有太大效果。

(5)选取聚类数量
这一节中将探讨K-Means算法如何去选择聚类数量或者说是如何选择参数K的值。
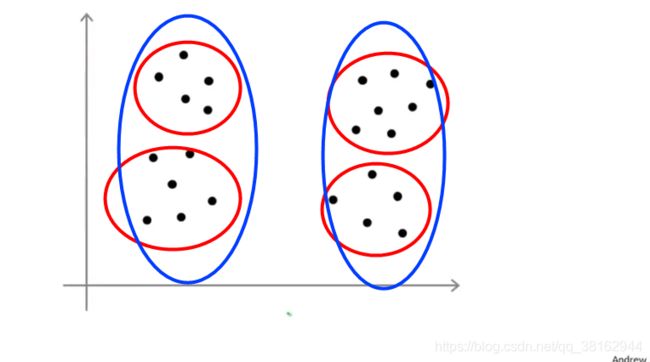
选择聚类数量并不容易,因为通常在数据集中有几个聚类是不清楚的,看下面这样的数据集,有时候会觉得有4个聚类,有时会觉得只有2个聚类。
正是因为这样的原因,用一个自动化的算法来选择聚类数量是很困难的。
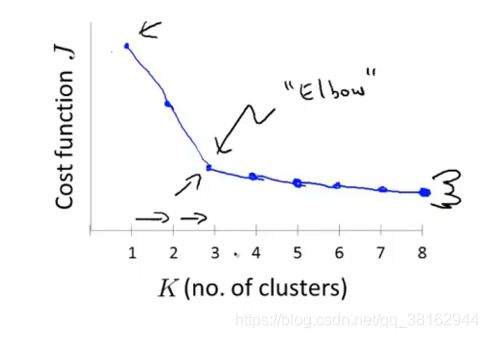
肘部法则:
当讨论选择聚类方法时,可能会谈到肘部法则这个方法,在肘部法则中,要做的是改变K也就是聚类总数,先用一个类来聚类,这就意味着所有的数据都会分到一个类里,然后计算代价函数J,用更多的类执行K-Means算法可能就会得到更小的J值,从下图中可以看到在K=3处有个突出来的部分,把这就叫作“肘部法则”。
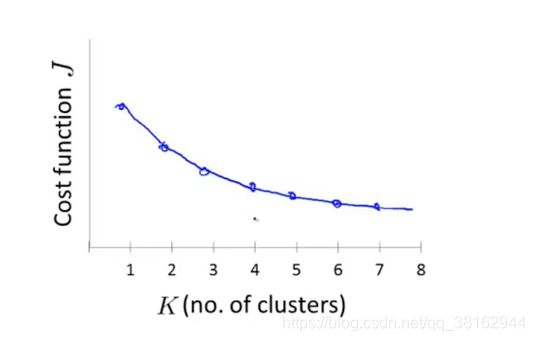
当应用“肘部法则”时,遇到类似上图,这将是一种用来选择聚类个数的合理方法,但是“肘部法则”并不常用的原因是在实际运用到聚类问题上时,往往最后会得到一条看上去相当模糊的曲线,如下图:
观察下图,看不到某个突出的点,看上去J值是连续下降的,所以这样并不能确定拐点合适的位置,这种情况下用“肘部法则”来选择聚类数目是很困难的。
另外一种选择K值的思路:决定聚类数量更好的方式是看哪个聚类数量能更好地适应后续的目的,下面用具体的例子解释。
思考,如果有5个分类,T恤能否更好地满足顾客的需求?可以卖出多少T恤?客户是否会感到满意?所以考虑到后续的发展,就可以帮助你来选择是3种尺码好一些还是用5种尺码更适合。
大部分时候聚类数量K仍然是通过手动、人工输入或者经验来决定的,一种可以尝试方式是“肘部法则”,但不能期望它每次都有效果,选择聚类数量更好的思路是问自己运行K-Means算法的目的是什么,然后再决定聚类数量K取多少更好地服务于后续的目的。