34. 在排序数组中查找元素的第一个和最后一个位置 ( 二分查找 时间复杂度 logn)
LeetCode: 34. 在排序数组中查找元素的第一个和最后一个位置
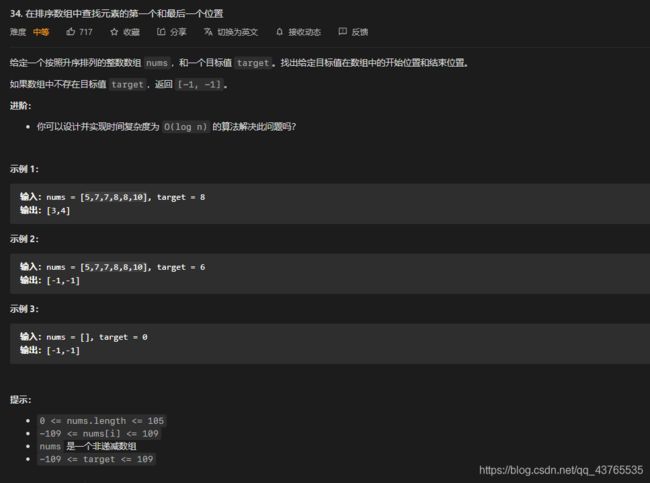
题目要求: 在已经排好序的数组中找出 target 的开始与结束下表。 找不到则输出 [ − 1 , − 1 ] [-1,-1] [−1,−1]
通过二分查找, 找到大于等于 target 的右边界下标, 找到第一个小于 target 的左边界下标
两次二分,知道左右边界后, 即可得到 target 的开始结束位置。
二分查找
最优解法 2 ∗ l o g n 2 * logn 2∗logn
class Solution {
public int[] searchRange(int[] nums, int target) {
int len = nums.length;
int left = bs(nums, 0, len - 1, target, false) + 1;
int right = bs(nums, 0, len - 1, target, true);
//
if(left > right || left < 0 || right >= len && nums[left] != target
|| nums[right] != target) return new int[]{
-1, -1};
return new int[]{
left, right};
}
public int bs(int[] arr, int start, int end, int target, boolean f){
int left = start, right = end;
int ans = -1;
while(left <= right){
int mid = (left + right) / 2;
if(arr[mid] < target || (f && arr[mid] <= target)){
left = mid + 1;
ans = mid;
} else {
right = mid - 1;
}
}
return ans;
}
}
通过查找出的下标,然后向前向后进行遍历相等的 target 直到左右边界的位置.
二分查找 AC Code
class Solution {
public int[] searchRange(int[] nums, int target) {
int len = nums.length;
int index = bs(nums, 0, len - 1, target);
int a = index, b = index;
// 最坏的情况是 nlogn
if(index == -1) return new int[]{
index, index};
while((a >= 0 && nums[a] == target) || (b < len && nums[b] == target)){
if(a >= 0 && nums[a] == target) a--;
if(b < len && nums[b] == target) b++;
}
return new int[]{
a + 1, b - 1};
}
public int bs(int[] arr, int start, int end, int target){
int left = start, right = end;
while(left <= right){
int mid = left + (right - left) / 2;
if(arr[mid] < target){
left = mid + 1;
} else if(arr[mid] > target){
right = mid - 1;
} else {
// 相等
return mid;
}
}
return -1;
}
}
时间复杂度: m l o g n mlogn mlogn >> m 取决于有几个与target相同的