我的西瓜书笔记之“人多力量大”——决策树与随机森林(上)
文章目录
- 《机器学习》笔记——决策树与随机森林
-
- 1. 简介
- 2. ID3算法
-
- 2.1 信息熵(Information Entropy)
- 2.2 条件熵(Conditional Entropy)
- 2.3 KL散度与信息增益(Kullback-Leibler Divergence & Information Gain)
- 2.4 ID3决策树
- 2.5 C4.5算法
-
- 2.5.1 简介
- 2.5.2 信息增益率
- 2.5 CART算法
-
- 2.5.1 简介
- 2.5.2 Gini指数
- 2.5.3 CART树的回归问题
- 后记
- 参考文献
决策树是传统机器学习中很重要的基本算法之一。决策树所需要的训练样本少,构建思路简单,训练所得的模型也可以通过graphviz和matplotlib等工具进行可视化操作,因此我们可以非常直观的对其进行解释。
《机器学习》笔记——决策树与随机森林
1. 简介
说到底,决策树还不是树,是树就是if-else语句。(bushi)

决策树是很典型的判别模型,常用的决策树有三种,分别是ID3树,C4.5树,CART树。三种类型的树的目标函数分别为互信息(Mutual Information),互信息率(Mutual Information Ratio)和Gini系数(Gini Coefficient)。其中互信息在决策树中也常被成为信息增益,其实后者是前者的无偏估计,二者在决策树算法中是等效的。
2. ID3算法
2.1 信息熵(Information Entropy)
话不多说直接上定义式
H ( x ) = − ∑ i = 1 n p i log p i H(\boldsymbol{x}) = -\sum\limits_{i=1}^{n}p_i\log p_i H(x)=−i=1∑npilogpi
信息熵越大,说明该事件包含的信息量越多,也就越难发生。举个不太恰当的例子,比如美国突然亡了,这件事情包含的信息量很大,所以短时间内不太容易发生;又比如你看完这篇文章会点个赞,这件事情包含的信息量比较小,所以很容易发生(doge)。
2.2 条件熵(Conditional Entropy)
条件熵可以类比条件概率来理解,其定义式为:
H ( Y ∣ X ) = H ( X , Y ) − H ( X ) = − ∑ x , y p ( x , y ) log ( y ∣ x ) H(Y|X) = H(X,Y)-H(X) = -\sum\limits_{x,y}p(x,y)\log(y|x) H(Y∣X)=H(X,Y)−H(X)=−x,y∑p(x,y)log(y∣x)
条件熵是推导出互信息的重要手段之一。关于熵的详细来源和推导可以参见香农著名的论文《A Mathematical Theory of Communication》
2.3 KL散度与信息增益(Kullback-Leibler Divergence & Information Gain)
KL散度又叫相对熵,是度量两个概率分布之间距离的指标。设有两个概率分布P(X), Q(X), 则KL散度的定义式为
D ( P ∣ ∣ Q ) = ∑ x p ( x ) log p ( x ) q ( x ) D(P||Q) = \sum\limits_xp(x)\log\frac{p(x)}{q(x)} D(P∣∣Q)=x∑p(x)logq(x)p(x)
显然当P(X) = Q(X)时D(P||Q) = 0,因为此时P(X)和Q(X)为同一分布,距离为0。
信息增益的定义为两个随机变量X,Y的联合分布和边缘分布的KL散度。定义式如下
I ( X , Y ) = ∑ x , y p ( x , y ) log p ( x , y ) p ( x ) p ( y ) I(X,Y) = \sum\limits_{x,y}p(x,y)\log\frac{p(x,y)}{p(x)p(y)} I(X,Y)=x,y∑p(x,y)logp(x)p(y)p(x,y)
当且仅当P(X),Q(X)相互独立时I(X,Y) = 0。另外,信息增益还可以根据信息熵和条件熵得出,其定义式为
I ( X , Y ) = H ( X ) + H ( Y ) − H ( X , Y ) = H ( X ) − H ( X ∣ Y ) I(X,Y) = H(X)+H(Y)-H(X,Y) = H(X)-H(X|Y) I(X,Y)=H(X)+H(Y)−H(X,Y)=H(X)−H(X∣Y)
跟条件概率一样,用一张图能更好理解信息增益
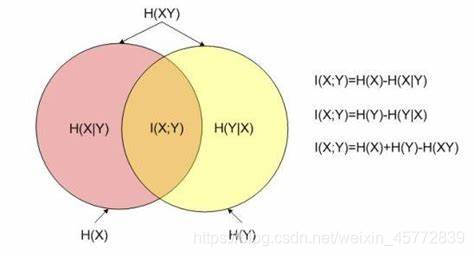
2.4 ID3决策树
ID3决策树的叶节点就是根据信息增益来确定的,每一层对所有未被选择所有属性计算信息增益,选出最大的一个作为该层的叶节点。以西瓜数据集2.0为例

显然,开始时分为正例和反例,其中正例 p 1 = 8 17 p_1 = \frac{8}{17} p1=178,反例 p 2 = 9 17 p_2 = \frac{9}{17} p2=179,则信息熵
H ( X ) = − ( 8 17 log 8 17 + 9 17 log 9 17 ) = 0.998 H(X) = -(\frac{8}{17}\log\frac{8}{17}+\frac{9}{17}\log\frac{9}{17}) = 0.998 H(X)=−(178log178+179log179)=0.998
要计算信息增益则还需要计算每个属性的信息熵,以色泽为例,色泽为青绿的瓜有6个,其中好瓜3个,则令色泽青绿为 D 1 D_1 D1
H ( D 1 ) = − ( 3 6 log 3 6 + 3 6 log 3 6 ) = 1 H(D_1) = -(\frac{3}{6}\log\frac{3}{6}+\frac{3}{6}\log\frac{3}{6}) = 1 H(D1)=−(63log63+63log63)=1
同理可得色泽乌黑( D 2 D_2 D2),色泽浅白( D 3 D_3 D3)的信息熵为
H ( D 2 ) = 0.918 H ( D 3 ) = 0.722 \begin{aligned} H(D_2) = 0.918\\ H(D_3) = 0.722 \end{aligned} H(D2)=0.918H(D3)=0.722
根据信息增益定义式有
I ( X , D ) = H ( X ) − H ( X ∣ Y ) = 0.998 − ( 6 17 × 1 + 6 17 × 0.918 + 5 17 × 0.722 ) = 0.109 \begin{aligned} I(X,D) = H(X)-H(X|Y) = 0.998-(\frac{6}{17}\times1+\frac{6}{17}\times0.918+\\\frac{5}{17}\times0.722) = 0.109 \end{aligned} I(X,D)=H(X)−H(X∣Y)=0.998−(176×1+176×0.918+175×0.722)=0.109
同理可以计算根蒂的信息增益为0.143,敲声为0.141,纹理为0.381,脐部为0.289,触感为0.006。其中属性“纹理”的信息增益最大,故将“纹理”作为节点。下一层的计算,将在“纹理=清晰,模糊和稍糊”的三种情况下分别计算剩余属性的条件熵,再利用信息增益的定义式计算每个属性的信息增益,如此往复,直至到达迭代次数或者所有特征全部被选择完毕。
从上面的例子中我们可以总结出一条规律:互信息=上一层的信息熵-下一层的信息熵。不过需要注意的是,除了根节点,每一层的信息熵都要当成条件熵进行计算,而决策树的任务就是需要找到最大信息熵来选取中间节点或者叶节点。因此,决策树或者由决策树构成的随机森林可以用来筛选特征并输出特征重要性。
思考:若是多分类问题且类别较多,ID3决策树模型的效果将会大幅削弱,因为此时信息增益将趋近于0
2.5 C4.5算法
2.5.1 简介
由于ID3算法对于连续值的处理无能为力,我们需要另一种改进的算法来实现对连续值的分类。C4.5作为ID3的改进算法,引入信息增益率作为其标准,结合信息增益本身来选择分裂子节点。
2.5.2 信息增益率
凡是加了个“率”字的名词,就是在其原来的基础上从变化量变为变化量除以原来的值,那么信息增益率的式子也很容易得出
I ( X , Y ) R a t i o = I ( X , Y ) H ( Y ) I(X,Y)_{Ratio} = \frac{I(X,Y)}{H(Y)} I(X,Y)Ratio=H(Y)I(X,Y)
根据信息熵的定义不难看出,信息增益率对取值数目少的特征由“偏好性”,即该特征取值数量越少,H(Y)往往会越小,反之越大。因此C4.5并不是暴力地取信息增益率最大的一项特征作为子节点,而是首先要选出高于所有特征的平均信息增益的几项,再从这几项中选出信息增益率最大的特征。
总而言之,C4.5算法执行过程大概可以总结为:
1. 计算所有未被选取的特征的信息增益;
2. 计算这些信息增益的平均值;
3. 选取信息增益大于平均值的特征;
4. 比较第3步中选出来的特征的信息增益率并选取最大的那一个,反回第一步,直至达到要求迭代次数或选择完毕。
2.5 CART算法
2.5.1 简介
CART算法全称是Classification and Regression Tree。顾名思义,这种算法既可以做分类也可以做回归。无论是在sklearn.tree的
DecisionTreeClassifier/DecisionTreeRegressor,还是在sklearn.ensemble中的RandomForestClassifier/RandomForestRegressor都是用CART树作为默认参数输入(当然也可以手动修改为ID3或C4.5)。
2.5.2 Gini指数
Gini指数本来是国际上通用的、用以衡量一个国家或地区居民收入差距的常用指标,但也可以作为机器学习决策树的目标函数,其定义式如下:
G i n i = ∑ k = 1 K p k ( 1 − p k ) = 1 − ∑ k = 1 K p k 2 Gini = \sum\limits_{k=1}^{K}p_k(1-p_k) = 1-\sum\limits_{k=1}^{K}p_k^2 Gini=k=1∑Kpk(1−pk)=1−k=1∑Kpk2
其中 p k p_k pk为某一特征的某一取值在该特征中所有取值中出现的概率。
类比Gini指数本身的作用,我们常常希望一个国家或地区的收入差距越小越好,因此我们就选用Gini指数最小的特征作为最优划分项。
2.5.3 CART树的回归问题
CART树在解决分类问题时选用Gini指数作为节点分裂标准,而在解决回归问题的时候则会选择传统的均方误差作为分类函数,不过回归树模型与一般的回归模型有所不同。
我们知道树的最后会生成若干个叶节点作为结果,那么类比线性回归就可以得到CART目标函数
a = arg min a 1 n ∑ i = 1 n ( f ( x i ) − y ) 2 a = \argmin\limits_a \frac{1}{n}\sum\limits_{i = 1}^n(f(\boldsymbol{x}_i)-y)^2 a=aargminn1i=1∑n(f(xi)−y)2
当然这只是第一步,回归树面临的还有一个重大问题:如何选取划分点?
有一个最简单的方法——二分法,即选定一个阈值t,将样本分为大于t的部分和小于t的部分。这两个部分分别拥有自己的均方误差值,而CART回归树要做的就是使得这两个回归树的均方误差之和最小。t值的选取也很容易,显然我们可以知道t值是位于分界点处两个样本取值之间的一个值,常常是这两个样本取值正中间的值,即
t = a i + a i + 1 2 t = \frac{a_i+a_{i+1}}{2} t=2ai+ai+1
我们可以遍历所有的样本来选取t值,譬如最开始t是 a i a_i ai和 a i + 1 a_{i+1} ai+1之间的值,即小于t的样本有 a 1 , a 2 a_1,a_2 a1,a2… a i a_i ai,大于t的样本有 a i + 1 , a i + 2 . . . a n a_{i+1},a_{i+2}...a_n ai+1,ai+2...an,可以用一张图来表示
对于左边,回归树可以给出预测值 c 1 c_1 c1,对于右边,同样有预测值 c 2 c_2 c2。现在只要遍历i的所有取值,求出均方误差值之和最小的那一个。即
i = arg min i [ min c 1 ∑ k = 1 i ( c 1 − y ) 2 + min c 2 ∑ k = i + 1 n ( c 2 − y ) 2 ] i = \argmin_i[\min\limits_{c_1}\sum\limits_{k=1}^i(c_1-y)^2+\min\limits_{c_2}\sum\limits_{k=i+1}^n(c_2-y)^2] i=iargmin[c1mink=1∑i(c1−y)2+c2mink=i+1∑n(c2−y)2]
这就是第一次选取分裂节点的过程,此后只需对左右两边的样本分别再次执行同样的操作,直到达到迭代次数。
后记
这篇笔记真的憋了很久,写的时候才发现之前学的很多细节性的东西都忘光了,如果文中有错误欢迎提出指正,另外复习真的很重要呀!!
参考文献
[1]周志华.机器学习[M].清华大学出版社:北京,2016.
[2]Jeremy Liang.机器学习算法笔记--------建立西瓜数据集[EB/OL].https://blog.csdn.net/qq_35654046/article/details/84783638
2018-12-04.
[3]wuliytTaotao.[EB/OL]. https://www.cnblogs.com/wuliytTaotao/p/10724118.html.2019-4-1在这里插入图片描述
