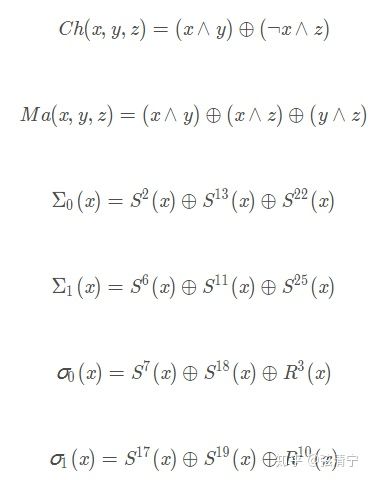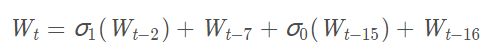区块链 试题_区块链期末复习四
之前已经把主要部分看完了(我觉得应该差不多了叭)。接下来要开始扣一些细节,毕竟得考试,逐个击破之。
九、一些细节和试题
9.1 SHA256算法
这里直接搬运CSDN的文章,写的很好,点这个链接。
https://blog.csdn.net/u011583927/article/details/80905740blog.csdn.net我写一些我自己能看懂的话。
对于任意长度的消息,SHA256都会产生一个256bit长的哈希值,称作消息摘要。分几步走战略(滑稽)
9.1.1常量初始化
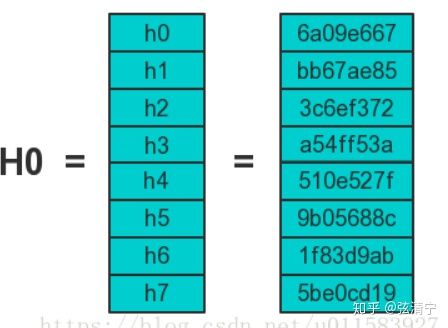
SHA256算法中会用到8个哈希初值以及64个哈希常量。这八个初始值如下。
这些初值是对自然数中前8个质数(2,3,5,7,11,13,17,19)开平方根,对其小数部分取前32bit而来。例如根号2约为0.414213562373095048,而
比较这个和上述图片的第一行。
在SHA256算法中,用到的64个常量如下:
和8个哈希初值类似,这些常量是对自然数中前64个质数的立方根的小数部分取前32bit而来。
9.1.2信息预处理
SHA256算法中的预处理就是在想要Hash的消息后面补充一些特定信息,使整个消息满足指定的结构。信息的预处理分为两个步骤:附加填充比特和附加长度。
1)附加填充比特
在报文末尾进行填充,使报文长度在对512取模以后的余数是448。填充是这样进行的:先补第一个比特为1,然后都补0,直到长度满足对512取模后余数是448。需要注意的是,信息必须进行填充,也就是说,即使长度已经满足对512取模后余数是448,补位也必须要进行,这时要填充512个比特。因此,填充是至少补一位,最多补512位。
举个栗子:以信息“abc”为例显示补位的过程。
a,b,c对应的ASCII码分别是97,98,99
于是原始信息的二进制编码为:01100001 01100010 01100011
补位第一步,首先补一个“1” : 0110000101100010 01100011 1
补位第二步,补423个“0”:01100001 01100010 01100011 10000000 00000000 … 00000000
补位完成后的数据如下(为了简介用16进制表示):
这时候会有个小问题,为什么是余448。这是因为在第一步的预处理后,第二步会再附加上一个64bit的数据,用来表示原始报文的长度信息。而448+64=512,正好拼成了一个完整的结构。
2)附加长度值
附加长度值就是将原始数据(第一步填充前的消息)的长度信息补到已经进行了填充操作的消息后面。SHA256用一个64位的数据来表示原始消息的长度。长度信息的编码方式为64-bit big-endian integer,就是所谓的大端存储,百度一下就好了。这里举个小栗子。比如存0x123456,正常存储就是0x123456,而大端存储就会存成0x563412这样子,两个数字占一个字节,所以56占一个字节,34一个,12一个,简单点说,就是按字节逆序存储。
9.1.3逻辑运算
SHA256散列函数中涉及的操作全部是逻辑的位运算,包括如下的逻辑函数:
上述符号的含义:
9.1.4计算消息摘要
现在来介绍SHA256算法的主体部分,即消息摘要是如何计算的。
首先:将消息分解成512-bit大小的块。
假设消息M可以被分解为n个块,于是整个算法需要做的就是完成n次迭代,n次迭代的结果就是最终的哈希值,即256bit的数字摘要。
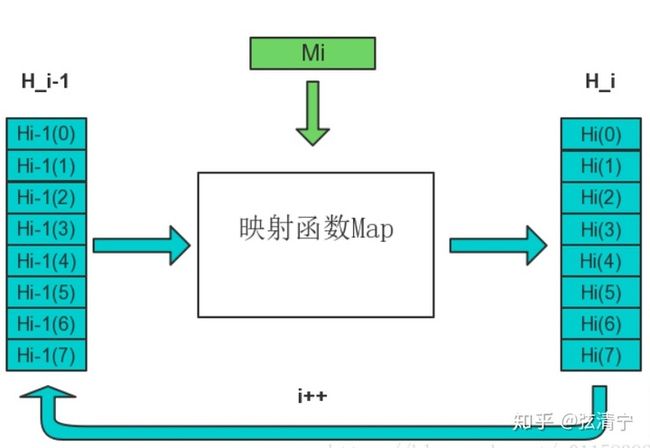
H0初值设置为前面介绍的8个哈希初值,经过第一个数据块进行运算,得到H1,即完成了第一次迭代H1经过第二个数据块得到H2,……,依次处理,最后得到Hn,Hn即为最终的256-bit消息摘要。
图中256-bit的Hi被描述8个小块,这是因为SHA256算法中的最小运算单元称为“字”(Word),一个字是32位。下面开始介绍每一次迭代的内容。
1)STEP1:构造64个字(word)
对于每一块Mi,将其分解为16个32-bit的big-endian的字,记为w[0], …, w[15],也就是说,前16个字直接由消息的第i个块分解得到,而我们总共需要构造64个字,故其余的48个字由如下迭代公式得到:
于是经过这些我们就得到了W1,W2,...,W64。
2)STEP2:进行64次循环
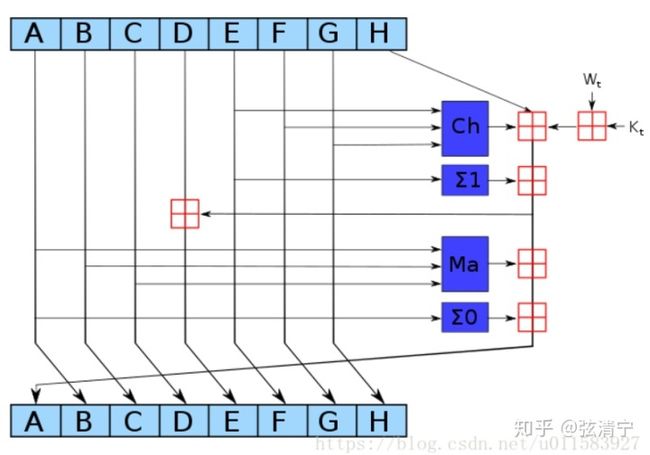
映射 Map包含了64次加密循环,每次加密循环可以由下图描述:
图中,ABCDEFGH这8个字(word)在按照一定的规则进行更新,其中深蓝色方块是事先定义好的非线性逻辑函数,详细定义看9.1.3里的图;红色方块是取模运算(mod2^32);ABCDEFGH一开始的初始值分别为H{i-1}(0),H{i-1}(1),…,H{i-1}(7) ;Kt是第t个密钥,对应我们上文提到的64个常量;Wt就是刚刚得到的那些Wt。这个过程进行64次以后,就完成了这一块的迭代。
开始第二块迭代的时候,把第一块迭代结束的值当做第二块初始值灌入第二次迭代的开始,持续像第一次迭代那样。通过迭代n次对ABCDEFGH这八个字进行加密(其实整个算法过程进行了64n次),最后输出的8个字就是SHA256哈希后的值。
9.2几种攻击方式
9.2.1女巫攻击
这种攻击主要是恶意节点创造出很多节点,对于P2P网络而言,拥有很多节点主要是用于冗余和备份,如果攻击者创造出很多节点,相当于控制了网络的一大部分,可以破坏冗余策略和备份策略。
9.2.2拒绝服务
如果Alice非常讨厌Bob,她不愿意为Bob提供服务,譬如在自己创建的区块中,Alice就会故意忽略掉Bob相关的交易。但即使Alice在一个区块中忽略了Bob的交易,其他诚实的矿工会在交易中包括Bob的交易。
9.2.3双重支付
这个在之前就写过,不写了。
9.2.4 51%攻击
掌握了51%的算力就相当于掌控了区块链。(莫名想起掌控雷电233333)
9.3DH算法
老师上课用很大篇幅去讲了,应该学会。先上图。
原理:DH协商过程,Alice和Bob首先挑选一个颜色(黄色),这个颜色是可以公开的(每次通信不同);然后再各自挑选一个秘密的颜色(Alice橙色,Bob青色)。然后Alice和Bob各自将自己的秘密颜色和黄色进行混合,得到了另外的两个颜色(Alice橙褐色,Bob淡蓝色)。Alice和Bob分别将自己的颜色发给对方。Alice和Bob在收到对方发来的颜色后,再分别和自己的颜色相混合,此时,两人得到了一个相同的颜色(黄褐色)。
在这个过程中,攻击者Eve可以一直监听网络,并且获得Alice和Bob在网络上交换的所有信息。也即,可以获得黄色、橙褐色、淡蓝色这些信息。阻止Eve获得最终的黄褐色的是Alice和Bob分别挑选的秘密颜色(说白了就是因为有这个秘密颜色所以Eve得不到最终的秘密—黄褐色),橙色和青色。也即,需要能够证明,即使Eve得到了黄色和橙褐色,Eve也不能推导出Alice的秘密颜色。
郭老师写的很清楚了,就不慢慢码字了23333。
先定义一下原根。
定义:取整数a和素数p,如果有
然后再讲DH算法。
其实最本质的就是最后的那个等式。证明就按定义来就好了,下面复习一下欧拉定理。
9.4欧拉定理
在叙述欧拉定理之前,先叙述欧拉函数的一些性质。
性质1:若a为质数,则
性质2:若p为质数,则
性质3:
这里立刻可以得到一个推论。
推论:若
欧拉定理:若n和a为正整数且n和a互质,则有
由欧拉定理,可以立刻推出费马小定理。
费马小定理:若a是不能被质数p整除的正整数,则有
9.5RSA算法及其原理
上课貌似让写过一次,所以还是把这个写一写叭,花了一个小时梳理了一遍,证明很简单,但有些繁琐。字丑,随便看看吧。
这里用的是这篇文章,写的特别特别特别仔细。
密码学基础1:RSA算法原理全面解析www.jianshu.com这里模逆那里需要扩展欧几里得算法求,后来的k就是第一页那个y。最后那个证明里用到了欧拉定理和费马小定理。这个RSA算法其实就是用了模运算的性质和几个定理。上边那篇文章里还提及中国剩余定理,这可是为数不多以中国开头的定理。
9.6MPT树
在以太坊中的MPT树中,树节点可以分为以下四类:
- 空节点:(represented as the empty string)
- 分支节点:A 17-item node
[ v0 ... v15, vt ] - 叶子节点:A 2-item node
[ encodedPath, value ] - 扩展节点:A 2-item node
[ encodedPath, key ]
空节点,简单的表示空,在代码中是一个空串。
叶子节点(leaf),表示为[key,value]的一个键值对,其中key是key的一种特殊十六进制编码,value是value的RLP编码。
扩展节点(extension),也是[key,value]的一个键值对,但是这里的value是其他节点的hash值,这个hash可以被用来查询数据库中的节点。也就是说通过hash链接到其他节点。
分支节点(branch),因为MPT树中的key被编码成一种特殊的16进制的表示,再加上最后的value,所以分支节点是一个长度为17的list,前16个元素对应着key中的16个可能的十六进制字符,如果有一个[key,value]对在这个分支节点终止,最后一个元素代表一个值,即分支节点既可以搜索路径的终止也可以是路径的中间节点。
9.6.1三种编码方式
Raw编码就是原生的key值,不做任何改变。这种编码方式的key,是MPT对外提供接口的默认编码方式。例如一条key为“cat”,value为“dog”的数据项,其Raw编码就是['c', 'a', 't'],换成ASCII表示方式就是[63, 61, 74],这里数字是16进制。
Hex编码:从Raw编码向Hex编码的转换规则是:
- 将Raw编码的每个字符,根据高4位低4位(nibble)拆成两个字节;
- 若该Key对应的节点存储的是真实的数据项内容(即该节点是叶子节点),则在末位添加一个ASCII值为16的字符作为终止标志符;
- 若该key对应的节点存储的是另外一个节点的哈希索引(即该节点是扩展节点),则不加任何字符;
key为“cat”, value为“dog”的数据项,其Hex编码为[6, 3, 6, 1, 7, 4, 10]
Hex编码用于对内存中MPT树节点key进行编码
HP编码:HP编码是在Hex编码基础上发展的,注意到节点有三类(排除空节点),一类是叶子节点,一类是扩展节点,还有一类分支节点。而叶子节点和扩展节点具有相同的数据结构,从而我们只需要在编码时候区分两种节点即可。再考虑奇偶问题,所以需要四种前缀(假设当前有两个路径分别是‘136’和‘0136’,在存储的时候可能是没有办法区分的)。HP编码将Hex中在叶子节点之后加的10删掉了,所以其实是在Raw编码基础上搞的事情。
HP编码的规则如下:
- 若原key的末尾字节的值为16(即该节点是叶子节点),去掉该字节;
- 在key之前增加一个半字节,其中最低位用来编码原本key长度的奇偶信息,key长度为奇数,则该位为1;低2位中编码一个特殊的终止标记符,若该节点为叶子节点,则该位为1;
- 若原本key的长度为偶数,则在key之前再增加一个值为0x0的半字节;
- 将原本key的内容作压缩,即将两个字符以高4位低4位进行划分,存储在一个字节中(Hex扩展的逆过程);
9.6.2两个习题
若Hex编码为[6, 3, 6, 1, 7, 4, 10],则HP编码的值为[20, 63, 61, 74]
下面是两个栗子。
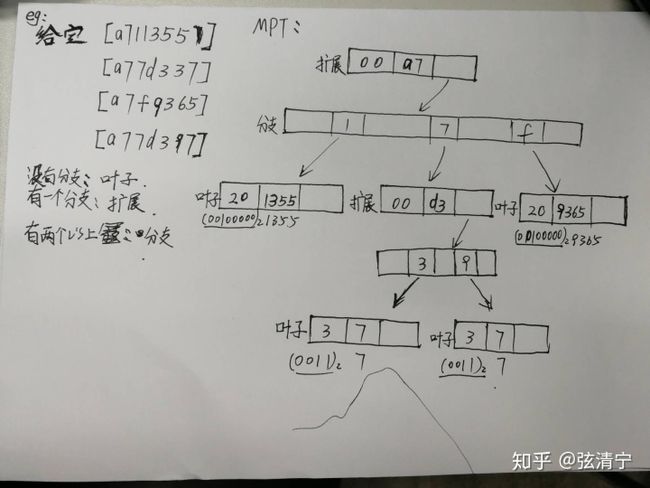
栗子1:
栗子2:
9.7什么时候该用区块链
9.8两种攻击
9.8.1THE DAO
老师写的代码太长了,简洁一点写个栗子。
withdraw();//将存款移除
Addr.call.value(1)();
fallback();//跳转执行withdraw()
Balance[Addr] -= 1;上述就是fallback函数的攻击精髓,其实就是每当要在执行余额减去1的时候,就又跳到一开始去执行移出存款操作。
这种代码执行方式可以称为push,而我们解决这种问题需要做pull。
举个例子理解push和pull这两种概念,假如参加你参加一场拍卖会,拍卖场这么规定,竞价者将其所付的钱在竞价时就交给拍卖场,如果出现更高价,则退还上一个竞价者的钱,这个退还的过程,可以是有两种,第一种称为push,也就是拍卖场将钱主动给你退还回来,第二种称为pull,就是你自己去拍卖场的后台拿你的钱,这是两种截然不同的处理方式。
这里是第四个函数Balance执行的减钱操作(这就是push,系统主动去做)。
郭老师的一堆代码解释THE DAO,这里只说结论。
从代码看,本次攻击得以成功的因素有二:一是dao余额扣减和Ether转账这两步操作的顺序有误,二是不受限制地执行未知代码。
9.8.2Fomo3d游戏
“5哥”是怎么拿到这笔奖金的,原理很简单。设置很高的gas limit和gas price,导致短时间内矿工只会对这个gas price很高的交易进行处理,而设置很高的gas limit又会使得即使处理过程很长,也能一直处理下去。因此,在短时间内不会有新的买“彩票”成功的人,“5哥”得以赢得最后的奖金。
——————————————————————————————————————
以太坊那篇文章写了一点点,觉得郭老师那篇已经写得很好了,我也不必花大力气去再写一篇。以太坊白皮书读不大懂,后面涉及的名词太多,如果以后做这方面的工作,倒是可以慢慢研究一番。(修改于2019.11.18.21:56)