python xgb模型 预测_XGBoost使用PMML部署的预测偏差

在使用xgboost时偶然发现python预测的结果和pmml预测的结果在小数位上存在差异，部分样本在6-7位小数位开始出现，即小数位上的数字不同，当样本足够多时，甚至可能在4-5位出现差异。如下面例子所示：

这个偏差不是偶然的的，刘建平Pinard在《用PMML实现机器学习模型的跨平台上线》中说PMML加载得到的模型和算法库自己独有的模型相比，预测会有一点点的偏差，知乎问题《如何看待pmml标准在机器学习和深度学习领域的地位？》下SofaSofa.io也说了目前java和python的convergence时不时会有万分之一的小误差。

为说明该精度差异具有普遍性，下面使用泰坦尼克号的数据集进行测试。

首先先说明两点:

1. XGBoost使用的是32位浮点，而其他模型是64位浮点，这个本质区别会使两者的精度差异不同。
2. XGboost预测结果是由这两步得到的：经过所有子树路径的叶结点值统计和 ==》 使用sigmoid函数将和转换为概率值。

下面测试过程可以在 https://github.com/lizhigu1996/xgboost_precision_explore/tree/master/test 中复现。

1. XGboost python与pmml文件的预测

1.1 直接预测结果对比

首先对数据集进行一个预处理，类别变量进行LabelEncoder（由于TICKET列比较特殊，java读取csv时不好读取该列，LabelEncoder后便于读取），其中训练集用于训练，测试集用于验证误差。

生成pmml文件需先用PMMLPipeline进行封装，再用sklearn2pmml导出pmml文件。DataFrameMapper过程为数值型变量不处理，类别性变量进行独热编码，并忽略未出现过的值。代码如下：

# 数据映射
mapper = DataFrameMapper(
    [(num_cols, None)] + [([char_col], [CategoricalDomain(invalid_value_treatment='as_is'),
                                        OneHotEncoder(handle_unknown='ignore')]) for char_col in char_cols])
# 训练模型
xgb = XGBClassifier(random_state=1234)
xgb_pmml = PMMLPipeline([('mapper', mapper), ('model', xgb)])
xgb_pmml.fit(X_train, Y_train)

# 导出pmml模型文件
sklearn2pmml(xgb_pmml, r"model_file/xgb_pmml.pmml", with_repr=True)

# 直接使用PMMLPipeline封装的管道预测，该预测在python上等同于Pipeline封装，所以不另外用Pipeline封装去预测
xgb_predict_python = pd.DataFrame(xgb_pmml.predict_proba(X_test)).rename(columns={
      0:'proba_0', 1:'proba_1'})
xgb_predict_python['PASSENGERID'] = X_test['PASSENGERID'].values
xgb_predict_python.to_csv(r'python_predict/xgb_predict_python.csv')

# 调用jar包运行pmml模型
run_pmml_jar('java -jar pmml_predict/runpmml.jar data/X_test.csv model_file/xgb_pmml.pmml pmml_predict/xgb_predict_pmml.csv PASSENGERID')

将python预测结果和python预测结果按照字符型读取csv，避免读取后python自动使部分变量有精度损失（直接读取容易在精度上有细微差异， 比如0.12141读取成0.12141001，关于python的精度损失可以查看为什么浮点数不正确？），并且字符型也便于小数位的比较。

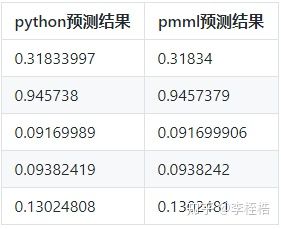
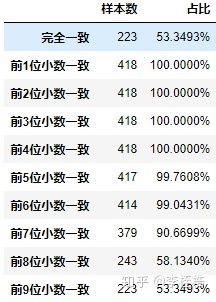
python预测结果和pmml预测结果对比如下，发现从第5位小数位开始出现差异：

下面为第5位小数位和第6位小数位有差异的样本，可以看到python预测结果和pmml预测结果的差异非常之小，但还是存在差异：

再看一下第7位小数位有差异的部分样本：

这个精度差异不是由pmml的结构引起，JPMML-XGBoost是从XGBoost的二进制存储文件里加载各节点的score，它是可以非常精准的将XGBoost树结构准换成pmml的，正如作者所说这是绝对正确的（issues 32）。

1.2 叶子节点和对比

为了探索是什么原因导致python和pmml文件的预测存在精度差异，我们看一下是在XGBoost模型预测结果的计算过程中的哪一步除了问题。

1. 经过所有子树路径的叶结点值统计和
2. 使用sigmoid函数将和转换为概率值

pmml对XGBoost的转换应该保证这两步的结果是相同的，下面查看各子树的叶节点的值是否有精度损失，但查看每个子树的叶结点值较为麻烦，直接查看所有子树叶节点的和是否有差异，如果无差异，每个子树的叶结点值也无差异。

为了计算所有子树叶结点值的和，python使用下面代码：

xgb_predict_python_margin = X_test[['PASSENGERID']]
xgb_predict_python_margin['margin'] = xgb_pmml._final_estimator.predict(mapper.transform(X_test), output_margin=True)
xgb_predict_python_margin.to_csv(r'python_predict/xgb_predict_python_margin.csv')

而pmml则需更改pmml文件才能得到所有子树叶结点值的和，只需在pmml文件的Output处增加下面代码即可：

这时即可让pmml输出所有子树叶结点值的和，在python中运行下面代码可修改pmml并预测：

modify_xgb_pmml('model_file/xgb_pmml.pmml', 'model_file/xgb_pmml_margin.pmml')
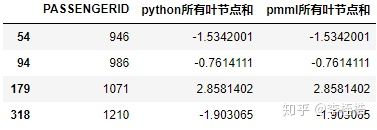
run_pmml_jar('java -jar pmml_predict/runpmml.jar data/X_test.csv model_file/xgb_pmml_margin.pmml pmml_predict/xgb_predict_pmml_margin.csv PASSENGERID')

通过比较的两个环境生成的csv文件，所有样本叶子节点和是完全相同的，一点精度差异都没有，说明python树结构和pmml树结构的叶子节点表示的数值是完全一致的。

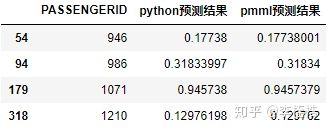
查看刚才在预测结果上第5位小数位和第6位小数位有差异的样本，在叶子节点和的计算上无差异：

也就是说python和pmml的预测精度差异并不在pmml对xgboost树结构的转换上，两者计算的所有子树叶结点值的统计和是完全相同的，是在下一步的sigmoid运算出现了精度差异。

1.3 sigmoid运算对比

由于XGBoost使用的是32位浮点，python和pmml的实现分别是：

• python：python默认的浮点运算为64位，在python中将所有子树叶结点值的和使用numpy.float32数组存储，并使用32位的np.exp实现sigmoid运算可得到与predictproba完全一致的结果。这里不管是存储还是运算，只要不是32位浮点（比如用numpy.float64位存储或者用np.exp(-x, np.float64)）都会导致结果出现差异，_这验证了XGBoost在c++的底层实现中的确是使用32位浮点，所以想要得到与XGBoost底层运算相同的结果，存储和运算过程都要在32位浮点的基础上进行，否则无法复现。代码如下：

sigmoid = lambda x: 1 / (1 + np.exp(-x))
np.float32(sigmoid(np.float32(python_predict['python所有叶节点和']))).astype(str)

• pmml：pmml同样默认64位浮点运算，为了得到32位浮点运算需要将所有子树叶结点值的和使用dataType=”float”存储，并通过x-mathContext=”float”告诉PMML引擎需要切换到32位浮点模式（issues 15），sigmoid运算使用的是normalizationMethod=”logit”。

而为了知道pmml的sigmoid运算具体是哪一步出了问题，分别对pmml文件进行下面三种修改：

1. OutputField删除dataType=”float”，修改为如下：

2. RegressionModel删除x-mathContext=”float”，修改为如下：

 
..... 

3. RegressionModel删除x-mathContext="float"，且OutputField删除dataType="float"，修改为如下：

.....
 
 
.....

依旧是刚才在预测结果上第5位小数位和第6位小数位有差异的样本，加上三种修改的情况后如下：

上面的关系是：

• pmml修改后预测结果1 限制了 dataType=”float” 得到 pmml预测结果
• pmml修改后预测结果3 限制了 dataType=”float” 得到 pmml修改后预测结果2
• pmml修改后预测结果3 限制了 x-mathContext=”float” 得到 pmml修改后预测结果1

所以可以看出使用 normalizationMethod=”logit” 去做sigmoid运算得到的结果应该是 pmml修改后预测结果1 和 pmml修改后预测结果3，也就是说目前XGBoos的pmml文件预测的结果其实是在做了sigmoid运算得到一个64位浮点数后，再通过 dataType=”float” 转换成了32位浮点数。

再具体看一下pmml对于两个步骤的具体过程，首先pmml文件的 模块（对应XGBoost预测的步骤1）得到所有子树叶结点值的统计和，这个值使用32位浮点保存，在pmml中的代码如下：

...
    

           
    
...

然后在 模块（对应XGBoost预测的步骤2）对 xgbValue 进行sigmoid运算，并且将结果转换成32位浮点数，在pmml中的代码如下：

...
    
    
        
        
    
        

        
        
    
...

所以xgboost的pmml计算过程应该是：

1. 计算所有子树叶结点值的32位浮点统计和
2. 对和进行sigmoid运算得到64位浮点概率值
3. 将64位浮点概率值转换为32位浮点概率值

至于第三步这个转换过程与python的64位浮点至32位浮点的转换是一致的，可通过下面代码验证：

np.float64(xgb_predict_pmml_test['pmml修改后预测结果1']).astype(np.float32).astype(str)

而对于 normalizationMethod=”logit” 具体做了什么可以查看PMML 4.3 - Regression，他的计算公式是和python相同的，probability(1)和probability(0)的计算如下：

• p1 = 1 / ( 1 + exp( -y1 ) )
• p2 = 1 - p1

当没有切换到32位浮点模式x-mathContext=”float”时，pmml和python的差别是：pmml和python对于叶节点和都是使用32位浮点存储，但是pmml做的是64位sigmoid运算，而python是做了32位sigmoid运算。通过下面的测试可以看到的确是这样。

首先运行下面代码，看一下numpy计算的差别，：

sigmoid1 = lambda x: 1 / (1 + np.exp(-x))
sigmoid2 = lambda x: 1 / (1 + np.exp(-x, dtype=np.float32))
sigmoid3 = lambda x: 1 / (1 + np.exp(-x, dtype=np.float64))

print('np.float32数组的默认sigmoid运算:', sigmoid1(np.float32([-1.5342001]))[0],
      '结果类型:', sigmoid1(np.float32([-1.5342001]))[0].dtype)
print('np.float32数组的32位sigmoid运算:', sigmoid2(np.float32([-1.5342001]))[0],
      '结果类型:', sigmoid2(np.float32([-1.5342001]))[0].dtype)
print('np.float32数组的64位sigmoid运算:', sigmoid3(np.float32([-1.5342001]))[0],
      '结果类型:', sigmoid3(np.float32([-1.5342001]))[0].dtype, 'n')
print('np.float64数组的默认sigmoid运算:', sigmoid1(np.float64([-1.5342001]))[0],
      '结果类型:', sigmoid1(np.float64([-1.5342001]))[0].dtype)
print('np.float64数组的32位sigmoid运算:', sigmoid2(np.float32([-1.5342001]))[0],
      '结果类型:', sigmoid2(np.float32([-1.5342001]))[0].dtype)
print('np.float64数组的64位sigmoid运算:', sigmoid3(np.float64([-1.5342001]))[0],
      '结果类型:', sigmoid3(np.float64([-1.5342001]))[0].dtype)

# 输出如下
np.float32数组的默认sigmoid运算: 0.17738 结果类型: float32
np.float32数组的32位sigmoid运算: 0.17738 结果类型: float32
np.float32数组的64位sigmoid运算: 0.17737999597524234 结果类型: float64

np.float64数组的默认sigmoid运算: 0.1773799919316838 结果类型: float64
np.float64数组的32位sigmoid运算: 0.17738 结果类型: float32
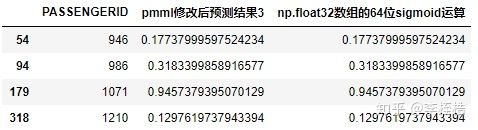
np.float64数组的64位sigmoid运算: 0.1773799919316838 结果类型: float64

所以如果我们要复现pmml用32位浮点保存叶节点和后使用64位sigmoid运算的这个过程，用下面代码就可以得到：

xgb_predict_python_test = xgb_predict_pmml_test[['PASSENGERID', 'pmml修改后预测结果3']]
xgb_predict_python_test['np.float32数组的64位sigmoid运算'] = sigmoid3(np.float32(python_predict['python所有叶节点和'])).astype(str)

一样查看在一开始预测结果上第5位小数位和第6位小数位有差异的样本：

可以看到完全一致，经过测试，是所有样本的计算都是一致的。也就是说，python使用32位浮点存储叶子节点和并用64位sigmoid运算的结果是和pmml没有加入 x-mathContext=”float” 的预测结果相同的。而当xgboost默认做32位sigmoid运算时，pmml的 x-mathContext=”float” 并不能在底层上同样实现正确的32位sigmoid运算。

我们再看一下不加 x-mathContext=”float” 的pmml预测结果进行32位浮点的转换与python预测的精度差异程度：

精度损失程度小于XGBoost默认的pmml预测结果，所以JPMML-XGBoost为了让pmml切换到32位浮点模式加入了 x-mathContext=”float” ，但是得到的结果精度损失反而超过了未加 x-mathContext=”float” 的情况。

那么pmml加入 x-mathContext=”float” 后到底是做了什么？

先重述一下JPMML-XGBoost的issues 15的内容，PMML 4.3的规范实际是没有属性 x-mathContext=”float” 的，但是PMML规范允许第三方扩展元素和属性，它们与标准元素的区别是名称带有 X- 和 x- 前缀（详见Extension Mechanism），而 x-mathContext=”float” 的详情在 http://mantis.dmg.org/view.php?id=179 中讨论，但很遗憾，我无法注册账号，注册的验证码一直不显示，使用其他电脑也不行，所以无法探究 x-mathContext=”float” 到底是做了什么操作。作者在这里说加入 x-mathContext=”float” 通知PMML引擎切换到32位浮点模式后就能够在pmml中精确地重现XGBoost预测，但经过测试并不能，这里我曾以为是不是我的JAR包有错误，但是使用了官方的例子跟踪和报告预测，在python中用jpmml_evaluator库去预测时，和我得到的结果一样，所以并不是我的JAR包错误。（由于JAVA版本问题，本机未安装jpmml_evaluator成功，直接在linux服务器运行的，所以该段代码不在xgboost_precision_explore.py中）复现代码如下：

from jpmml_evaluator import make_evaluator
from jpmml_evaluator.py4j import launch_gateway, Py4JBackend

# Launch Py4J server
gateway = launch_gateway()
backend = Py4JBackend(gateway)
evaluator = make_evaluator(backend, "xgb_pmml.pmml", reporting = True).verify()

arguments = {
      
    "PCLASS" : 1,
    "NAME" : 124,
    "SEX" : 1,
    "AGE" : 25.0,
    "SIBSP" : 0,
    "PARCH" : 0,
    "TICKET" : 99,
    "FARE" : 26.0,
    "CABIN" : 186,
    "EMBARKED" : 0
}

print(arguments)

results = evaluator.evaluate(arguments)
print(results)

# Shut down Py4J server
gateway.shutdown()

2 LightGBM python与pmml文件的预测

为了与XGBoost进行对比，同时测试LightGBM的情况，但是相同的代码LightGBM却没有精度差异，对比情况如下（由于LightGBM是64位浮点，直接对比17位小数）：

看结果有5个样本完全不同，但这其实是JAVA运行pmml将结果输出成科学计数法造成的，实际无差异。

其实不是所有的LightGBM模型都是没有精度差异的，只是这个模型的python和pmml预测结果恰好一致而已，一般LightGBM模型也会有精度差异，但是差异非常之小，一般在15位小数后，而且样本非常之少，在1%左右，这个是可以接受的误差。

对于LightGBM模型的pmml转换，有兴趣可以查看LightGBM作者与jpmml-lightgbm作者的讨论issues 31，这里有关于LightGBM精度差异的一些解释，因为底层实现与XGBoost不同，精度差异的原因也是完全不同的，这里我就没有对LightGBM模型的精度差异的具体原因进行探索了，有兴趣的可自行研究。

3 总结

综上，由于XGBoost使用的是32位浮点，而pmml使用的是64位浮点，pmml树结构的各节点score因为只涉及到和运算，可以通过XGBoost的二进制文件精准转换得到，但是sigmoid运算却无法得到准确的32位浮点运算的结果，就算使用了第三方扩展属性 x-mathContext=”float” 通知PMML引擎切换到32位浮点模式也无法精确地重现XGBoost预测，目前XGBoost精度差异无法避免，有两点使用建议：

1. 在python中使用 model._final_estimator.predict(mapper.transform(data), output_margin=True) 得到所有子树叶节点值的统计和后，手动计算64位浮点sigmoid运算 sigmoid = lambda x: 1 / (1 + np.exp(-x, dtype=np.float64)) ，同时在pmml文件中删除RegressionModel中的x-mathContext=”float”，且删除OutputField中的dataType=”float”，可以保证python和pmml的预测结果相同。
2. 不进行任何改动，但是使用到预测结果的阈值需要进行分组时，阈值不能过于精准，建议四舍五入至4位小数，否者阈值是0.09169989时，python预测了0.09169989，但是pmml却预测出0.091699906，会使线上线下分组结果不统一。