[ python ] 动态规划笔记 [一] 四大步骤
动态规划组成部分一: 确定状态
【状态】
在动态规划中属于定海神针
一般来说,解动态规划的时候需要开一个数组f,数组的每个元素f[i]、f[i][j]意味着什么,类似于数学题中X、Y、Z代表着什么
【确定状态】需要两个意识
- 最后一步
- 子问题
![[ python ] 动态规划笔记 [一] 四大步骤_第1张图片](http://img.e-com-net.com/image/info8/3da247e6ccc248fcae84c730f3bd573e.jpg)
比如在这道题中:
![[ python ] 动态规划笔记 [一] 四大步骤_第2张图片](http://img.e-com-net.com/image/info8/7a021e5ba9554064b000b2dea65d9520.jpg)
【关键点】
1、我们现在并不关心前面ak-1、k-1是什么,但是我们可以确定,前面的硬币组合肯定拼出来27-ak
2、拼出27-ak的个数一定要最少
所以 -------------------->
1、我们要求用最少的硬币数拼出27-ak
2、值得一提的是,原问题是拼出27
3、我们把原问题转化成了一个子问题,而且规模更小:27-ak
4、为了简化定义,我们设状态 f(X)=最少用多少枚硬币拼出X,所以原问题是找出f(27),现在是找出f(27-ak)
以上为【确定状态的部分】
现在,我们不知道最后那一步的硬币面值是多少,是2 是5 是7?
![[ python ] 动态规划笔记 [一] 四大步骤_第3张图片](http://img.e-com-net.com/image/info8/682d1a09cda14f3ea8500328e28bcf03.jpg)
下面是递归解法:
class Solution:
'''
面值2 5 7
'''
def pay(self, sum):
res = float('inf')
if sum == 0:
return 0
if sum >= 2:
res = min(res,self.pay(sum-2)+1)
if sum >= 5:
res = min(res,self.pay(sum-5)+1)
if sum >= 7:
res = min(res,self.pay(sum-7)+1)
return res
a = Solution()
print(a.pay(27))
但是,会出现重复递归:
![[ python ] 动态规划笔记 [一] 四大步骤_第4张图片](http://img.e-com-net.com/image/info8/d7cad03376eb478f893d9659ce016bab.jpg)
如何避免?
要将计算结果保存下来->请看动态规划组成部分二
动态规划组成部分二: 转移方程
动态规划组成部分三:初试条件和边界情况
动态规划组成部分四:计算顺序
class Solution:
'''
面值1 2 5 7
'''
def pay(self, sum):
values = [1, 2, 5, 7]
memory = [float('inf')] * (sum+1)
memory[1], memory[2], memory[5], memory[7]= 1, 1, 1, 1
for i in range(3,sum+1):
if i not in values:
memory[i] = min(memory[i], memory[i-1]+1, memory[i-2]+1, memory[i-5]+1, memory[i-7]+1)
return memory[sum]
a = Solution()
print(a.pay(271))
class Solution:
def calculate(self,m,n):
map = [[0] * n for i in range(m)]
map[0][0] = 1
'''
目的地是:
map[m-1][n-1]
'''
for i in range(1, n):
map[0][i] = map[0][i-1]
for i in range(1, m):
map[i][0] = map[i-1][0]
for i in range(1,m):
for j in range(1,n):
map[i][j] = map[i-1][j] + map[i][j-1]
return map[i][j]
sol = Solution()
print(sol.calculate(10,10))
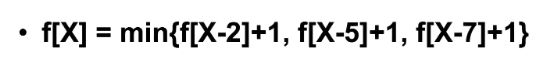
![[ python ] 动态规划笔记 [一] 四大步骤_第5张图片](http://img.e-com-net.com/image/info8/e70576a739d8496bab6a0528e4a52061.jpg)
![[ python ] 动态规划笔记 [一] 四大步骤_第6张图片](http://img.e-com-net.com/image/info8/3a26af3b2d0843359f4bb6252f5067f0.jpg)
![[ python ] 动态规划笔记 [一] 四大步骤_第7张图片](http://img.e-com-net.com/image/info8/c638cf69e78a47d8aa88649eb31bd4e0.jpg)
![[ python ] 动态规划笔记 [一] 四大步骤_第8张图片](http://img.e-com-net.com/image/info8/20dbbbb9ab7c45b7913aab2ec0d902a4.jpg)
![[ python ] 动态规划笔记 [一] 四大步骤_第9张图片](http://img.e-com-net.com/image/info8/cb816711158a40f0aca67093e6d473eb.jpg)
![[ python ] 动态规划笔记 [一] 四大步骤_第10张图片](http://img.e-com-net.com/image/info8/c2e14e9f9ffa4897b16bd7e887e0c505.jpg)
![[ python ] 动态规划笔记 [一] 四大步骤_第11张图片](http://img.e-com-net.com/image/info8/11212ff12d604e038763a774e605e4fe.jpg)
![[ python ] 动态规划笔记 [一] 四大步骤_第12张图片](http://img.e-com-net.com/image/info8/8b7bc63d29964c73bf370cbbfe96a3fd.jpg)
![[ python ] 动态规划笔记 [一] 四大步骤_第13张图片](http://img.e-com-net.com/image/info8/5b3a42c5198141c6844635d8c900087c.jpg)
![[ python ] 动态规划笔记 [一] 四大步骤_第14张图片](http://img.e-com-net.com/image/info8/9410fb994a6447d5af0fcb09033c8196.jpg)