基于遗传算法的TSP算法

一、理论基础

TSP(traveling salesman problem,旅行商问题)是典型的NP完全问题，即其最坏情况下的时间复杂度随着问题规模的增大按指数方式增长，到目前为止还未找到一个多项式时间的有效算法。
TSP问题可描述为：已知$n$个城市相互之间的距离，某一旅行商从某个城市出发访问每个城市有且仅有一次，最后回到出发城市，如何安排才使其所走路线距离最短。简言之，就是寻找一条最短的遍历$n$个城市的路径，或者说搜索自然子集$X=\{1,2,\cdots ,n\}$($X$的元素表示对$n$个城市的编号)的一个排列$\pi (X)=\{V_1,V_2,\cdots ,V_n\}$，使得$$T_d=\sum _{i=1}^{n+1}d(V_i,V_{i+1})+d(V_n,V_1)$$取得最小值，其中$d(V_i,V_{i+1})$表示城市$V_i$到城市$V_{i+1}$的距离。

二、案例背景

1，问题描述

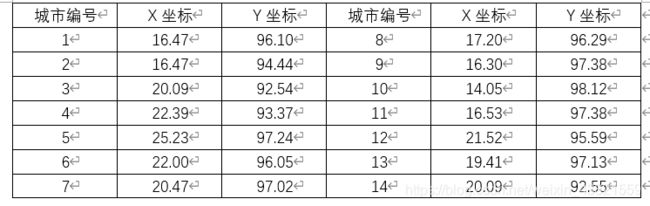
本案例以14个城市为例，假定14个城市的位置坐标如表1所列。寻找出一条最短的遍历14个城市的路径。

表1 14个城市的位置坐标

2，解决思路和步骤

(1).算法流程

遗传算法TSP问题的流程图如图1所示。

图1 遗传算法TSP问题求解的流程图

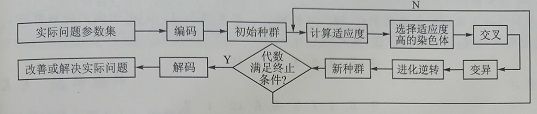
(2).遗传算法实现

<1>编码
采用整数排列编码方法。对于$n$个城市的TSP问题，染色体分为$n$段，其中每一段为对应城市的编号，对10个城市的TSP问题$1,2,3,4,5,6,7,8,9,10$，则$|1|10|2|4|5|6|8|7|9|3$就是一个合法的染色体。
<2>种群初始化
在完成染色体编码以后，必须产生一个初始种群作为起始解，所以首先需要决定初始化种群的数目。初始化种群的数目一般根据经验得到，一般情况下种群的数量视城市规模的大小而定，其取值在50~200之间浮动。
<3>适应度函数
设$k_1|k_2|\cdots |k_i|\cdots |k_n|$为一个采用整数编码的染色体，$D_{k_i{k}_j}$为城市$k_i$到城市$k_j$的距离，则该个体的适应度为$$fitness=\frac{1}{\sum _{i=1}^{n-1}{D}_{k_i{k}_j}+D_{k_n{k}_1}}$$即适应度函数为恰好走遍$n$个城市再回到出发城市的距离的倒数。优化的目标就是选择适应度函数值尽可能大的染色体，适应度函数值越大的染色体越优质，反之越劣质。
<4>选择操作
选择操作即从旧群体中以一定概率选择个体到新群体中，个体被选中的概率跟适应度值有关，个体适应度值越大，被选中的概率越大。
<5>交叉操作
采用部分映射杂交，确定交叉操作的父代，将父代样本两两分组，每组重复以下过程(假定城市数为10)：
①产生两个$[1,10]$区间内的随机整数$r_1$和$r_2$，确定两个位置，对两位置的中间数据进行交叉，如$r_1=4,r_2=7$
$$951|3742|1086$$$$1054|6387|219$$交叉为$$951|6387|10\ast \ast$$$$105\ast |3742|\ast 19$$②交叉后，同一个个体中有重复的城市编号，不重复的数字保留，有冲突的数字(带$\ast$位置)采用部分映射的方法消除冲突，即利用中间段的对应关系进行映射。结果为$$951|6387|1042$$$$1058|3742|619$$<6>变异操作
变异策略采取随机选取两个点，将其对换位置。产生两个$[1,10]$范围内的随机整数$r_1$和$r_2$，确定两个位置，将其对换位置，如$r_1=4,r_2=7$$$951|6|38|7|1042$$变异后为$$951|7|38|6|1042$$<7>进化逆转操作
为改善遗传算法的局部搜索能力，在选择、交叉、变异之后引进连续多次的进化逆转操作。这里的“进化”是指逆转算子的单方向性，即只有经过逆转后，适应度值有提高的才接受下来，否则逆转无效。
产生两个$[1,10]$区间内的随机整数$r_1$和$r_2$，确定两个位置，将其对换位置，如$r_1=4,r_2=7$$$951|738|61042$$进化逆转后为$$951|837|61042$$对每个个体进行交叉变异，然后代入适应度函数进行评估，$x$选择出适应度值大的个体进行下一代的交叉和变异以及进化逆转操作。循环操作：判断是否满足设定的最大遗传代数MAXGEN ，不满足则跳入适应度值的计算；否则，结束遗传操作。

三、MATLAB程序实现

(1).种群初始化

种群初始化函数InitPop的代码：

function Chrom = InitPop(NIND,N)
%% 初始化种群
% 输入：
% NIND：种群大小
% N：   个体染色体长度（这里为城市的个数）  
% 输出：
% 初始种群
Chrom = zeros(NIND, N);         % 用于存储种群
for i = 1:NIND
    Chrom(i, :) = randperm(N);    % 随机生成初始种群
end

(2).适应度函数

求种群个体的适应度函数Fitness的代码：

function FitnV = Fitness(len)
%% 适应度函数     
% 输入：
% 个体的长度（TSP的距离）
% 输出：
% 个体的适应度值
FitnV = 1./len;

(3).选择操作

选择操作函数Select的代码：

function SelCh = Select(Chrom,FitnV,GGAP)
%% 选择操作
% 输入
% Chrom 种群
% FitnV 适应度值
% GGAP：选择概率
% 输出
% SelCh  被选择的个体
NIND = size(Chrom,1);                         % 种群个数
NSel = max(floor(NIND*GGAP+.5), 2);   % 被选中个体的数目
ChrIx = Sus(FitnV,NSel);                 % 被选中的个体索引号
SelCh = Chrom(ChrIx, :);                  % 被选中的个体

其中，函数Sus的代码为：

function NewChrIx = Sus(FitnV,Nsel)
% 输入:
% FitnV  个体的适应度值
% Nsel   被选择个体的数目
% 输出:
% NewChrIx  被选择个体的索引号
% Identify the population size (Nind)
   [Nind,ans] = size(FitnV);
% Perform stochastic universal sampling
   cumfit = cumsum(FitnV);
   trials = cumfit(Nind) / Nsel * (rand + (0:Nsel-1)');
   Mf = cumfit(:, ones(1, Nsel));
   Mt = trials(:, ones(1, Nind))';
   [NewChrIx, ans] = find(Mt < Mf & [ zeros(1, Nsel); Mf(1:Nind-1, :) ] <= Mt);
% Shuffle new population
   [ans, shuf] = sort(rand(Nsel, 1));
   NewChrIx = NewChrIx(shuf);   
% End of function

(4).交叉操作

交叉操作函数Recombin的代码：

function SelCh = Recombin(SelCh,Pc)
%% 交叉操作
% 输入
% SelCh  被选择的个体
% Pc     交叉概率
% 输出：
% SelCh 交叉后的个体
NSel = size(SelCh, 1);
for i = 1:2:NSel-mod(NSel, 2)
    if Pc >= rand         %  交叉概率Pc
        [SelCh(i, :), SelCh(i+1, :)] = intercross(SelCh(i, :), SelCh(i+1, :));
    end
end
function [a, b] = intercross(a, b)
%% 交叉
% 输入：
% a和b为两个待交叉的个体
% 输出：
% a和b为交叉后得到的两个个体
L = length(a);
r1 = randsrc(1, 1, [1:L]);
r2 = randsrc(1, 1, [1:L]);
if r1 ~= r2
    a0 = a; b0 = b;
    s = min([r1, r2]);
    e = max([r1, r2]);
    for i = s:e
        a1 = a; b1 = b;
        a(i) = b0(i);
        b(i) = a0(i);
        x = find(a == a(i));
        y = find(b == b(i));
        i1 = x(x ~= i);
        i2 = y(y ~= i);
        if ~isempty(i1)
            a(i1) = a1(i);
        end
        if ~isempty(i2)
            b(i2) = b1(i);
        end
    end
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% %% 交叉算法采用部分匹配交叉
% 这部分代码有问题
% function [a, b] = intercross(a, b)
% L = length(a);
% r1 = ceil(rand * L);
% r2 = ceil(rand * L);
% if r1 ~= r2
%     s = min([r1,r2]);
%     e = max([r1,r2]);
%     a1 = a; b1 = b;
%     a(s:e) = b1(s:e);
%     b(s:e) = a1(s:e);
%     for i = [setdiff(1:L, s:e)]
%         [tf, loc] = ismember(a(i), a(s:e));
%         if tf
%             a(i) = a1(loc+s-1);
%         end
%         [tf, loc] = ismember(b(i), b(s:e));
%         if tf
%             b(i) = b1(loc+s-1);
%         end
%     end
% end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% function [a, b] = intercross(a, b)
% L = length(a);
% r1 = ceil(rand * L);
% r2 = ceil(rand * L);
% if r1 ~= r2
%     s = min([r1, r2]);
%     e = max([r1, r2]);
%     a1 = a; b1 = b;
%     a(s:e) = b1(s:e);
%     b(s:e) = a1(s:e);
%     for i = [setdiff(1:L, s:e)]
%         a2 = a1(~ismember(a1, a));
%         b2 = b1(~ismember(b1, b));
%         if ~isempty(a2) 
%             if ~isempty(find(a(s:e) == a(i), 1))
%                a(i) = a2(1);
%             end
%         end
%         if ~isempty(b2)
%             if ~isempty( find(b(s:e) == b(i), 1))
%                 b(i) = b2(1);
%             end
%         end
%     end
% end

(5).变异操作

变异操作函数Mutate的代码：

function SelCh = Mutate(SelCh, Pm)
%% 变异操作
% 输入：
% SelCh  被选择的个体
% Pm     变异概率
% 输出：
% SelCh 变异后的个体
[NSel, L] = size(SelCh);
for i = 1:NSel
    if Pm >= rand
        R = randperm(L);
        SelCh(i, R(1:2)) = SelCh(i, R(2:-1:1));
    end
end

(6).进化逆转操作

进化逆转操作Reverse的代码：

function SelCh=Reverse(SelCh,D)
%% 进化逆转函数
% 输入
% SelCh 被选择的个体
% D     个城市的距离矩阵
% 输出
% SelCh  进化逆转后的个体
[row, col] = size(SelCh);
ObjV = PathLength(D, SelCh);        % 计算路径长度
SelCh1 = SelCh;
for i = 1:row
    r1 = randsrc(1, 1, [1:col]);
    r2 = randsrc(1, 1, [1:col]);
    mininverse = min([r1 r2]);
    maxinverse = max([r1 r2]);
    SelCh1(i, mininverse:maxinverse) = SelCh1(i, maxinverse:-1:mininverse);
end
ObjV1 = PathLength(D, SelCh1);      % 计算路径长度
index = ObjV1 < ObjV;
SelCh(index, :)= SelCh1(index, :);      % 取距离较短者

(7).画路线轨迹图

画出所给路线的轨迹图函数DrawPath的代码：

function DrawPath(Chrom,X)
%% 画路径函数
%输入
% Chrom  待画路径   
% X          各城市坐标位置
R = Chrom(1, :);       %一个随机解(个体)
figure;
hold on
plot([X(R, 1); X(R(1), 1)], [X(R, 2); X(R(1), 2)], 'o', 'color', [0.5,0.5,0.5])
plot(X(R(1), 1), X(R(1), 2), 'rv', 'MarkerSize', 20)
plot(X(R(end), 1), X(R(end), 2), 'rs', 'MarkerSize', 20)
text(X(R(1),1)+0.05, X(R(1),2)+0.05, ['   起点' num2str(R(1))], 'color', [1,0,0]);
text(X(R(end),1)+0.05, X(R(end),2)+0.05, ['   终点' num2str(R(end))], 'color', [1,0,0]);
for i = 1:size(X,1)
    if R(1) ~= i && R(end) ~= i
        text(X(i,1)+0.05, X(i,2)+0.05, num2str(i), 'color', [1,0,0]);
    end
end
A = [X(R, :); X(R(1), :)];
row=size(A,1);
for i=2:row
    [arrowx, arrowy] = dsxy2figxy(gca, A(i-1:i,1), A(i-1:i,2));     % 坐标转换
    annotation('textarrow', arrowx, arrowy, 'HeadWidth', 8, 'color', [0,0,1]);
end
hold off
xlabel('横坐标')
ylabel('纵坐标')
title('轨迹图')
box on

(8).遗传算法主函数

主函数名为GA_TSP，代码如下：

clear
clc
close all
load CityPosition1.mat
%% 初始化参数
NIND = 100;                  % 种群大小
MAXGEN = 200;            % 最大遗传代数
Pc = 0.9;                          % 交叉概率
Pm = 0.05;                       % 变异概率
GGAP = 0.9;                     % 代沟(Generation gap)
D = Distance(X);                 % 生成距离矩阵
N = size(D, 1);                     % (14*14)
%% 初始化种群
Chrom = InitPop(NIND, N);
%% 在二维图上画出所有坐标点
% figure
% plot(X(:,1),X(:,2),'o');
%% 画出随机解的路线图
DrawPath(Chrom(1,:), X)
%% 输出随机解的路线和总距离
disp('初始种群中的一个随机值:')
OutputPath(Chrom(1,:));
Rlength = PathLength(D,Chrom(1,:));
disp(['总距离：', num2str(Rlength)]);
disp('~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~')
%% 优化
gen = 0;
figure;
hold on; box on
xlim([0,MAXGEN])
title('优化过程')
xlabel('代数')
ylabel('最优值')
ObjV = PathLength(D,Chrom);  %计算路线长度
preObjV = min(ObjV);
while gen < MAXGEN
    %% 计算适应度
    ObjV = PathLength(D,Chrom);  % 计算路线长度
    % fprintf('%d   %1.10f\n',gen,min(ObjV))
    line([gen-1, gen], [preObjV, min(ObjV)]);
    preObjV = min(ObjV);
    FitnV = Fitness(ObjV);
    %% 选择
    SelCh = Select(Chrom,FitnV,GGAP);
    %% 交叉操作
    SelCh = Recombin(SelCh,Pc);
    %% 变异
    SelCh = Mutate(SelCh,Pm);
    %% 进化逆转操作
    SelCh = Reverse(SelCh,D);
    %% 重插入子代的新种群
    Chrom = Reins(Chrom,SelCh,ObjV);
    %% 更新迭代次数
    gen = gen+1 ;
end
%% 画出最优解的路线图
ObjV = PathLength(D,Chrom);  %计算路线长度
[minObjV, minInd] = min(ObjV);
DrawPath(Chrom(minInd(1), :), X)
%% 输出最优解的路线和总距离
disp('最优解:')
p = OutputPath(Chrom(minInd(1), :));
disp(['总距离：', num2str(ObjV(minInd(1)))]);
disp('-------------------------------------------------------------')

重插入子代得到新种群的函数Reins代码如下：

function Chrom = Reins(Chrom, SelCh, ObjV)
%% 重插入子代的新种群
% 输入：
% Chrom  父代的种群
% SelCh    子代种群
% ObjV     父代适应度
% 输出：
% Chrom  组合父代与子代后得到的新种群
NIND = size(Chrom, 1);
NSel = size(SelCh, 1);
[TobjV, index] = sort(ObjV);
Chrom = [Chrom(index(1:NIND-NSel), :); SelCh];

(9).结果分析

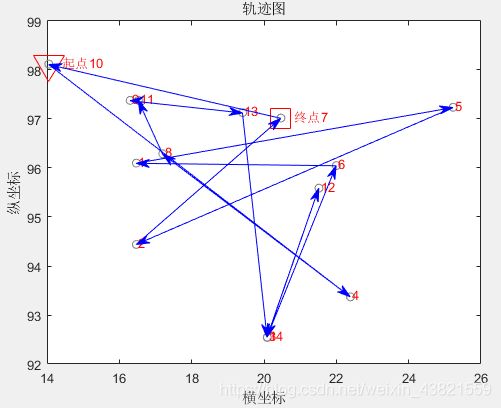
优化前的一个随机路线轨迹图如图2所示。

图2 随机路线图

初始种群中的一个随机值:
10—>4—>8—>11—>9—>13—>3—>12—>14—>6—>1—>5—>2—>7—>10
总距离：70.3719
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

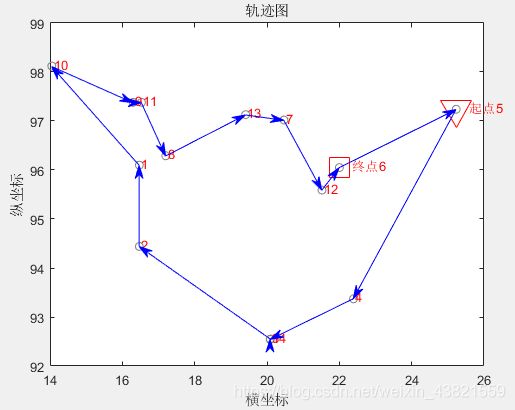
优化后的路线图如图3所示。

图3 最优解路线图

最优解:
5—>4—>3—>14—>2—>1—>10—>9—>11—>8—>13—>7—>12—>6—>5
总距离：29.3405
-------------------------------------------------------------

优化迭代图如图4所示。

图4 遗传算法进化过程图

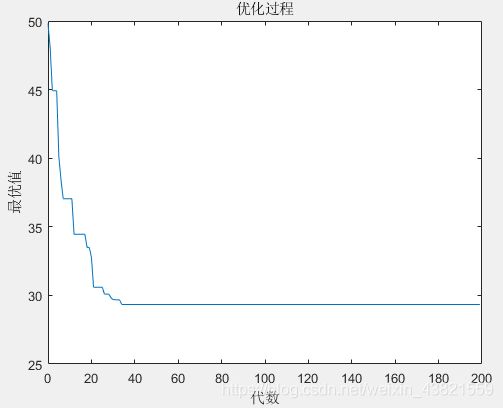
由优化图可以看出，优化前后路径长度得到很大改进，接近40代以后路径长度已经保持不变了，可以认为是最优解了，总距离由优化前的70.3719变为29.3405，减为原来的41.7%。

具体细节可参考：
链接：https://pan.baidu.com/s/16vnho_Uf6O1JdoVx9L2enQ
提取码：shgr

四、遗传算法的改进

上述程序中，对遗传算法做了以下两处改进。

1. 使用精英策略

子代种群中的最优个体永远不会比父代最优的个体差，这样使得父代的好的个体不至于由于交叉或者变异操作而丢失。

2. 使用进化逆转操作

同交叉算子相比较，逆转算子能使子代继承亲代的较多信息。

五、算法的局限性

当问题规模$n$比较小时，得到的一般都是最优解；当规模比较大时，一般只能得到近似解。这时可以通过增大种群大小和增加最大遗传代数使得优化值更接近最优解。

六、参考文献

[1] 储理才. 基于MATLAB的遗传算法程序设计及TSP问题求解[J]. 集美大学学报:自然科学版, 2001.
[2] 郁磊等. MATLAB智能算法30个案例分析(第2版)[M].北京航空航天大学出版社.2015年.