树及二叉树:java实现
争其必然,顺其自然
树
树是一种数据结构,它是由n(n>=1)个有限结点组成一个具有层次关系的集合。除了树的定义,其中还有树的一些概念,
空集合也是树,称为空树。空树中没有结点。
孩子结点或子结点:一个结点含有的子树的根结点称为该结点的子结点;
结点的度:一个结点含有的子结点的个数称为该结点的度;
叶结点或终端结点:度为0的结点称为叶结点;
非终端结点或分支结点:度不为0的结点;
双亲结点或父结点:若一个结点含有子结点,则这个结点称为其子结点的父结点;
兄弟结点:具有相同父结点的结点互称为兄弟结点;
树的度:一棵树中,最大的结点的度称为树的度;
结点的层次:从根开始定义起,根为第1层,根的子结点为第2层,以此类推;
树的高度或深度:树中结点的最大层次;
堂兄弟结点:双亲在同一层的结点互为堂兄弟;
结点的祖先:从根到该结点所经分支上的所有结点;
子孙:以某结点为根的子树中任一结点都称为该结点的子孙。
森林:由 棵互不相交的树的集合称为森林;
以上概念来自百度百科。这里就不深入展开,本人了解也有限,我们主要侧重于二叉树。
二叉树
二叉树(binary tree)是指树中节点的度不大于2的有序树(有序的体现在左右子树是有区别的)
二叉树的分类:
- 完全二叉树:在一棵二叉树中,除了最后一层,都是满的,并且最后一层或者是满的,或者是右边缺少连续若干节点,成为完全二叉树。
- 满二叉树。(深度为k,并且有 2^k -1 个节点的二叉树)
- 二叉查找树(Binary Search Tree)
- 平衡二叉树(Balanced Binary Tree)
- AVL树
- 红黑树(Red-black tree)
常用完全二叉树来学习树,因为它相对比较简单,其中也有一些性质
1、具有n个结点的完全二叉树的深度 [log2k +1](注:[ ]表示向下取整)
2、如果对一棵有n个结点的完全二叉树的结点按层序编号, 则对任一结点i (1≤i≤n) 有:
1.如果i=1, 则结点i是二叉树的根, 无双亲;如果i>1, 则其双亲parent (i) 是结点[i/2];
2.如果2i>n, 则结点i无左孩子, 否则其左孩子lchild (i) 是结点2i;
如果2i+1>n, 则结点i无右孩子, 否则其右孩子rchild (i) 是结点2i+1.
很多性质可以推导出来,不必死记硬背。
二叉树的创建
二叉树的存储方式可以通过链式存储与顺序存储方式。
顺序存储:

链式存储,每个节点存储自己的数据还会保存子节点的数据。
java对象属性如下
/**
* 左子节点
*/
private BiTreeNode leftNode;
/**
* 右子节点
*/
private BiTreeNode rightNode;
/**
* 节点数据
*/
private String data;
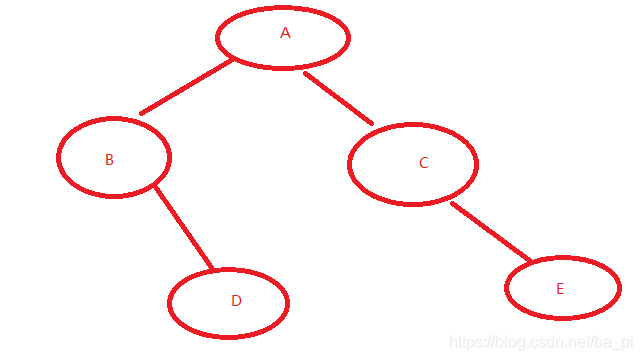
输入的时候节点的子节点为空定义为null,输入顺序为(“A”, “B”,null, “D”,null,null,“C”,null, “E”,null,null)
/**
* 前序遍历创建树
* @param strings
* @return
*/
public static BiTreeNode createTreeByFront(List<String> strings){
if (strings.isEmpty()){
return null;
}else {
BiTreeNode biTreeNode = new BiTreeNode();
String s = strings.get(0);
/**
* 字符串为null,该节点不存在
*/
if (s == null){
strings.remove(0);
return null;
}else {
/**
* 设置节点值
*/
biTreeNode.setData(s);
/**
* 移除第一个节点,如果包含大量节点,可以考虑linkedList,这里只为实现功能以及原理
*/
strings.remove(0);
/**
* 设置左右字节点
*/
biTreeNode.setLeftNode(createTreeByFront(strings));
biTreeNode.setRightNode(createTreeByFront(strings));
return biTreeNode;
}
}
}
创建树代码如下
List<String> strings = Arrays.asList("A", "B",null, "D",null,null,"C",null, "E",null,null);
/**
* 这里多做了一步操作,不是我吃饱了撑得哈,asList在使用remove方法的时候,会抛出 UnsupportedOperationException异常。
*/
List<String> data = new ArrayList<>(strings);
BiTreeNode treeByFront = createTreeByFront(data);
这里有朋友问了,为什么要多new ArrayList<>呀,我要解释一下多做的那一步操作,如果使用Arrays.asList创建出来的list,在remove的时候会抛出 UnsupportedOperationException异常。
/**
* Arrays类
**/
public static <T> List<T> asList(T... a) {
return new ArrayList<>(a);
}
/**
* ArrayList类 继承了AbstractList类
**/
private static class ArrayList<E> extends AbstractList<E>
implements RandomAccess, java.io.Serializable
{
private static final long serialVersionUID = -2764017481108945198L;
private final E[] a;
ArrayList(E[] array) {
a = Objects.requireNonNull(array);
}
/**
*AbstractList类调用remove方法会抛出异常
**/
public E remove(int index) {
throw new UnsupportedOperationException();
}
此时此刻我深刻的感受到"纸上得来终觉浅,绝知此事要躬行"。
二叉树的遍历
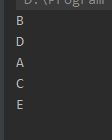
二叉树遍历方式有前序遍历,中序遍历,后序遍历。这里遍历的前中后代表的是根节点所在的位置,根节点在前,就是前序遍历,在中间,就是中序遍历。这里展示中序遍历,
实现代码如下:
/**
* 中序遍历
*/
public static void getOrderByMid(BiTreeNode node){
if (node == null){
return;
}else {
/**
* 遍历左子树
*/
getOrderByMid(node.getLeftNode());
System.out.println(node.getData());
/**
* 遍历右子树
*/
getOrderByMid(node.getRightNode());
}
}
最后附上git代码地址:https://gitee.com/zhoujie1/data-structure-and-algorithm.git
树有很多很多的应用,比如排序树,搜索树,红黑树等很多知识对于我来说也是知识盲区。在后面的时间里我再来扩充我的知识库。另外再说点题外话,写了很多废话,但是发现真有点用,至少在写总结的时候没那么难受了,哈哈,加油,打工人。