LeetCode每日一题01.25-01.31

2021.01.25-由斜杠划分区域959

由斜杠划分区域959

题目描述：

在由 1 x 1 方格组成的 N x N 网格 grid 中，每个 1 x 1 方块由 /、\ 或空格构成。这些字符会将方块划分为一些共边的区域。返回区域的数目。

题目解析：

连通性问题可使用BFS DFS 并查集，因为此题需要的是数目，并非连通的路径，所以推荐使用并查集

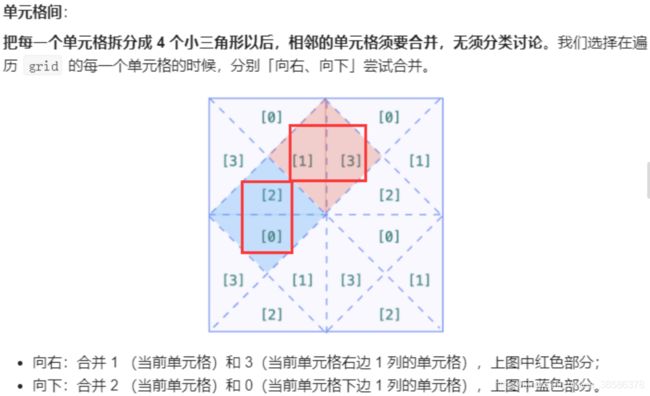
难点在于将1 x 1的方格根据grid分割为nn份的小方格，一个小方格由四个三角形构成，求区域即求4 * n *n个区域中连通的个数，一个三角形为一个节点，可分别从[向左，向上]、[向左，向下]、[向右，向上]和[向右、向下]进行分析，选择[向右，向下]遍历所有的节点，判断连通并计算连通图的个数
时间复杂度：O(N^2 log N) 双循环遍历+find父节点，空间复杂度O(N^2)

public class RegionsBySlashes {
     
    public int regionsBySlashes(String[] grid) {
     
        int length = grid.length;
        // 定义小三角形的个数
        int size = 4 * length * length;
        // 构造并查集
        UnionFind unionFind = new UnionFind(size);
        // i是行j是列，向右扩展j，向下扩展i
        for (int i = 0; i < length; i++) {
     
            // 二维转一维
            char[] row = grid[i].toCharArray();
            for (int j = 0; j < length; j++) {
     
                // 一个单元格的编号
                int index = 4 * (i * length + j);
                char c = row[j];
                // 单元格内合并
                if (c == '/') {
     
                    // 合并0 3;1 2
                    unionFind.union(index, index + 3);
                    unionFind.union(index + 1, index + 2);
                } else if (c == '\\') {
     
                    // 合并0 1；2 3
                    unionFind.union(index, index + 1);
                    unionFind.union(index + 2, index + 3);
                } else {
     
                    // 空格，合并0 1 2 3
                    unionFind.union(index, index + 1);
                    unionFind.union(index + 1, index + 2);
                    unionFind.union(index + 2, index + 3);
                }
                // 单元格间合并
                // 向右合并，当前单元格的1和右边单元格的3
                if (j + 1 < length) {
     
                    unionFind.union(index + 1, 4 * (i * length + j + 1) + 3);
                }
                // 向下合并，当前单元格的2和下边单元格的0
                if (i + 1 < length) {
     
                    unionFind.union(index + 2, 4 * ((i + 1) * length + j));
                }
            }
        }
        return unionFind.count;
    }
    public class UnionFind {
     
        // 记录每个节点的父节点
        int[] parent;
        // 记录独立节点的个数
        int count;
        /**
         * 初始化定义并查集的节点，其中每个节点的父节点初始值为下标值，即节点本身
         * @param n
         */
        public UnionFind(int n) {
     
            parent = new int[n];
            for (int i = 0; i < n; i++) {
     
                parent[i] = i;
            }
            // 初始定义所有的节点都是独立的
            count = n;
        }
        /**
         * 查找x的根节点；如果节点本身为根节点，直接返回x即可
         * @param x
         * @return
         */
        private int findRoot(int x) {
     
            int xRoot = x;
            while (xRoot != parent[xRoot]) {
     
                xRoot = parent[xRoot];
            }
            return xRoot;
        }
        /**
         * 合并两个节点，先找到x和y的根节点，如果相同则说明本身就是一个集合中的，不做任何处理；
         * 否则说明是独立的两个集合，做并集后count--
         * @param x
         * @param y
         */
        private void union(int x, int y) {
     
            int xRoot = findRoot(x);
            int yRoot = findRoot(y);
            // 发现不连通的节点，现在需要构造，则独立节点数--
            if (xRoot != yRoot) {
     
                parent[xRoot] = yRoot;
                count--;
            }
        }
    }
    public static void main(String[] args) {
     
        RegionsBySlashes regionsBySlashes = new RegionsBySlashes();
        String[] grid = {
     " /","/ "};
        System.out.println(regionsBySlashes.regionsBySlashes(grid));
    }
}

2021.01.26-等价多米诺骨牌对的数量1128

等价多米诺骨牌对的数量

题目描述：

给你一个由一些多米诺骨牌组成的列表 dominoes。

如果其中某一张多米诺骨牌可以通过旋转 0 度或 180 度得到另一张多米诺骨牌，我们就认为这两张牌是等价的。

形式上，dominoes[i] = [a, b] 和 dominoes[j] = [c, d] 等价的前提是 a=c 且 b=d，或是 a=d 且 b=c。

在 0 <= i < j < dominoes.length 的前提下，找出满足 dominoes[i] 和 dominoes[j] 等价的骨牌对 (i, j) 的数量。

题目解析：根据题目描述，是一个n*2的二维数组，现在需要以行遍历数组，判断是否有元素相同的行存在（元素相同指的是对于[a,b]，要么有[a,b]，要么有[b,a]

这里需要注意，对于一个行，和它等价的行之间也是相互等价的，例如a与b等价，a与c等价，那么b与c也等价，所以计算出a的等价数目，总等价数+=a的等价数目n(n+1)/2

一开始想的是用集合，因为没注意到只有两列，想着使用数组转集合，以及集合间reverse的方法。后续发现如果有多列的话，转集合的Lists接口不支持（需要导入外来包），需要手动遍历一行将元素加入集合中，操作麻烦；另外没有集合判等的方法，只有一个a.containsAll(b)方法，检查a是否是b的父集合

public class NumEquivDominoPairs {
     
    /**
     * 将二维数组转为一维的List集合，遍历一维数组，进行集合间的比较，
     * 判断集合是否相同/与其reverse结果是否相同，如果相同count++。遍历过的集合visited=true
     * 并且对于每一个的count，最后等价数量为count(count-1)/2，因为a与b等价，a与c等价，那么b和c也等价
     *
     * 不要忘记只有两列dominoes[i] = [a,b];
     * @param dominoes
     * @return
     */
    public int numEquivDominoPairs(int[][] dominoes) {
     
        // 根据题设条件二维数组长度最小为1，所以不判断dominoes.length是否为0
        if (dominoes == null || dominoes[0].length == 0) {
     
            return 0;
        }
        int length = dominoes.length;
        // 将二维数组转为一个一维集合数组
        List<Integer>[] rowList = new List[dominoes.length];
        // 初始化集合
        for (int i = 0; i < length; i++) {
     
            rowList[i] = new ArrayList<>();
        }
        for (int i = 0; i < length; i++) {
     
            rowList[i].add(dominoes[i][0]);
            rowList[i].add(dominoes[i][1]);
        }
        boolean[] visited = new boolean[length];
        for (int i = 0; i < length; i++) {
     
            visited[i] = false;
        }
        int result = 0;
        for (int i = 0; i < length; i++) {
     
            // 对于一个比较目标的等价个数
            int count = 0;
            if (!visited[i]) {
     
                visited[i] = true;
                for (int j = i + 1; j < length; j++) {
     
                    // containsAll方法判断两个集合是否元素相同（顺序无所谓）a.containsAll(b)判断a中是否包含b的全部元素（a为b的父集合）
                    if (!visited[j] && rowList[i].containsAll(rowList[j]) && rowList[j].containsAll(rowList[i])){
     
                        count++;
                        visited[j] = true;
                    }
                }
                count = count * (count + 1) / 2;
            }
            result += count;
        }
        return result;
    }

    public static void main(String[] args) {
     
        NumEquivDominoPairs numEquivDominoPairs = new NumEquivDominoPairs();
        int[][] dominoes = {
     {
     1,2},{
     2,1},{
     1,1},{
     1,2},{
     2,2}};
        System.out.println(numEquivDominoPairs.numEquivDominoPairs(dominoes));
    }
}

还有一个方法，利用HashSet元素唯一的性质，将每一行元素加入到hashSet中，set类型是int[]，当往集合中添加元素的时候会判断是否相等，如果相等则遇到等价行（需要重写set的hash和equals方法，因为反转也是相等的），则count++，否则直接加入。因为每一行可能对应多个对等行，所以使用Map集合类型，key为set存储一行数据，value为count存储对等个数，初始值为1
时间复杂度：O(N)O(N)，其中 NN 是输入数组的长度；空间复杂度：O(A)O(A)，这里 AA 是哈希表中键的总数

/**
     * 使用HashMap
     * @param dominoes
     * @return
     */
    public int numEquivDominoPairs(int[][] dominoes) {
     
        // 创建HashMap
        Map<Pair, Integer> dominoMap = new HashMap<>();
        // 遍历二维数组，将元素加入Map集合，二维转成一维遍历，使用foreach更为合适（不用确定每个行的具体位置）
        for (int[] domino : dominoes) {
     
            // 定义Pair
            Pair pair = new Pair(domino[0], domino[1]);
            // 将pair加入Map集合中
            // Map集合的getOrDefault(key,defaultValue)方法，如果key存在则返回get(key)，否则返回defaultValue
            // 如果key存在返回value+1并覆盖到pair的value中；如果不存在加入集合，value=1
            // set集合相同元素不能插入，add返回false；Map集合相同key可以插入，覆盖掉原有key-value
            dominoMap.put(pair,dominoMap.getOrDefault(pair,0) + 1);
        }
        // 定义结果对等数量
        int result = 0;
        // 遍历Map集合的value值，叠加计算总的对等数量
        for (int count : dominoMap.values()) {
     
            result += count * (count - 1) / 2;
        }
        return result;
    }

    /**
     * 定义hashSet集合
     */
    public class Pair {
     
        // 第一个元素
        int one;
        // 第二个元素
        int two;

        public Pair(int one, int two) {
     
            this.one = one;
            this.two = two;
        }

        // 判断是否相等，是先求hash然后求是否equals
        @Override
        public boolean equals(Object o) {
     
            if (this == o) return true;
            if (o == null || getClass() != o.getClass()) return false;
            Pair pair = (Pair) o;
            // 重新写相等的条件
            return (one == pair.one &&
                    two == pair.two) || (one == pair.two && two == pair.one);
        }

        @Override
        public int hashCode() {
     
            // 重新构造hash方法（两位数，让相同的数映射到同一位置）
            return one > two ? one * 10 + two : two * 10 + one;
        }
    }

参考：https://leetcode-cn.com/problems/number-of-equivalent-domino-pairs/solution/deng-jie-duo-mi-nuo-gu-pai-dui-de-shu-li-08z8/
第三种方法，因为是两位数，例如12和21，可以同一转为12，然后以行遍历。计算num=12，并且将其放置到数组count[num]中，这样每遇到一个相同的num都会count++，每次result+=count（1个对等，result=0+1；2个对象，result=0+1+2；三个对等，result=0+1+2+3.对于下一个行对等，又从0开始叠加到result）

时间复杂度：O(N)；空间复杂度O(A^2) A为二位数的最大值

    /**
     * 因为数据元素的范围为0-9，所以二位数最大值为99，给一个100长度的一维数组（00-99），存储对等个数
     * 将一行数据转为有序的二位数，遍历计算num，并存储数组中，num相同即下标对应数组值++
     * @param dominoes
     * @return
     */
    public int numEquivDominoPairs(int[][] dominoes) {
     
        // 定义二位数数组
        int[] nums = new int[100];
        // 定义结果对等值
        int result = 0;
        // 遍历二维数组
        for (int[] domino : dominoes) {
     
            // 统一定义为小值在十位，大值在个位
//            if (domino[0] > domino[1]) {
     
//                int temp = domino[0];
//                domino[0] = domino[1];
//                domino[1] = temp;
//            }
//            int num = domino[0] * 10 + domino[1];
            // 优化为三元表达式
            int num = domino[0] > domino[1] ? domino[1] * 10 + domino[0] : domino[0] * 10 + domino[1];
            // 起始值为0；如果之前已经有一个num（num对应值为1），那么这次遇到相同的即发现一个对等
            result += nums[num];
            // 在原有基础上++，记录每一个num的对等值个数
            nums[num]++;
        }
        return result;
    }