李宏毅2020机器学习作业一

Step1：读懂题目

题目的意思

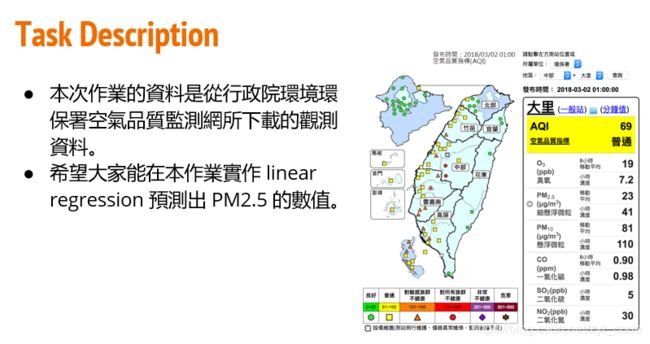
• 训练集是：12个月–>每月的前20天–>每天的24小时–>每小时的18种不同属性的数值
• 测试集：240天–>连续的9小时–>18种不同的属性
• 要求的输出：根据某天连续的9小时–>18种不同的属性，预测第10小时的PM2.5的值。也就是通过一个18*9的矩阵预测出来一个值

Step2：数据预处理

# 读取数据csv文件,将csv数据保存为矩阵
data = pd.read_csv('./train.csv', encoding='big5')  # read_csv顾名思义-读取csv文件    big5的编码是台湾和香港用的繁体
# print(data)
data = data.iloc[:, 3:]  # 要全部行、不要前三列
data[data == 'NR'] = 0  # FAINFULL的值原来是NR，现实意义中表示是否降雨那么可以用0 1 来表示
# print(data)
arr_data = data.to_numpy()  # 将data转换为numpy矩阵

数据处理到这里首先得到了一个二维的矩阵，一共有12*20*18行，每一行有24列
矩阵现在的结构是：

接下来要进一步处理数据，大致思想是把一个月的数据放到宏观的一行上去，这样一个月的小时就会一字排开，我们的实验是要求输入连续的9个小时的时间来预测第10小时的PM2.5值，放在一大行的好处就是可以有更多的连续9小时作为输入来训练。（我们将一个月的第一天到第二十天横向排序，那么我们可以使用滑动窗口的思想，取大小为9的窗口，从第一天的第0时一直可以划到第20天的第14时[为什么是14时，因为14+9=23，最后一个小时的PM2.5数据需要得到，所以这样处理可以最大化的利用已知训练集从而得到更多的数据]），画个图可能更好理解：
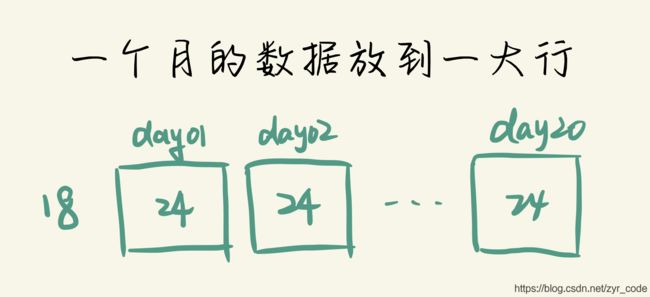首先把一个月放到一大行里，然后在慢慢滑动起始的时间，每9小时为为一组输入数据
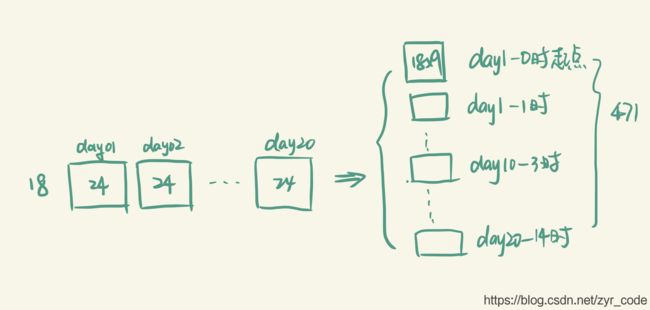最后，再把12个月放在一起。
下面我们用代码实现以上思想，因为第一次接触这样处理数据还比较抽象，所以这里是直接copy了老师的代码再去理解。

month_data = {
     }
for month in range(12):
    sample = np.empty([18, 480])  # 一行sample代表一个月的20天数据-->18行（18种不同属性，每一天24小时一共20天，所以共有480列）
    for day in range(20):
        sample[:, (day * 24):((day + 1) * 24)] = arr_data[18 * (20 * month + day):18 * (20 * month + day + 1), :]
        # 把一个月的所有天拼凑到一行上去
    month_data[month] = sample

# 生成新的训练集矩阵
x = np.empty([12 * 471, 18 * 9],
             dtype=float)  # 每个月一共480小时 但是为了最后的连续九个小时能有对应的结果 要留出9个小时的窗口 即只要471个小时的
# 列方面：我们需要通过一个18个属性*9小时的数据 来预测一个PM2.5的值-->这是一个矩阵呐！
y = np.empty([12 * 471, 1], dtype=float)
for month in range(12):
    for day in range(20):
        for hours in range(24):
            if day == 19 and hours > 14:
                continue
            x[month * 471 + day * 24 + hours, :] = month_data[month][:, day * 24 + hours:day * 24 + hours + 9].reshape(
                1, -1)
            y[month * 471 + day * 24 + hours, 0] = month_data[month][9, day * 24 + hours + 9]
            # x：month_data中的某月的某天某时开始的连续九个小时*18属性放到x里面 是一个矩阵最为x的第二列
            # y:它只需要属性的第十行（PM2.5）的第十个小时的值

reshape(1,-1):转换成一行
上述所有工作做完之后，X就是包含所有数据的数组，Y就是所有数据的结果，但此时还不可以进行训练，还需要两个步骤才可以。

Step3：Normalize与训练集分类

这里我们采用RMSE来进行分析
关于数据标准化可参考：https://www.cnblogs.com/chenyusheng0803/p/9867579.html

# 数据标准化--这里采用z标准化
mean_x = np.mean(x, axis=0)  # 18*9 , 求平均值
std_x = np.std(x, axis=0)  # 18*9， 求标准差
for i in range(len(x)):  # 471*12
    for j in range(len(x[0])):  # 18*9
        if std_x[j] != 0:
            x[i][j] = (x[i][j] - mean_x[j]) / std_x[j]

接下来是将训练数据按8:2拆成训练数据和验证数据。这样的好处是因为最终只给我们test data的输入而没有给我们输出，所以我们无法定量我们模型的好坏，而使用验证数据可以简单验证我们模型的好坏，让我们自己心里有数

# 将数据集分为8:2, 交叉验证
x_train_set = x[:math.floor(len(x) * 0.8), :]  # math.floor 是向下取整函数
y_train_set = y[:math.floor(len(y) * 0.8), :]
x_validation = x[math.floor(len(x) * 0.8):, :]
y_validation = y[math.floor(len(y) * 0.8):, :]

Step4: 训练模型

我们训练使用Loss function和梯度下降算法，直接上代码

# 训练模型--使用loss function 和gradient decent
dim = 18 * 9 + 1  # 用来做参数的维数，加1是为了对bias好处理（还有个误差项）。即最后的h(x)=w1x1+w2x2+'''+WnXn+b
w = np.ones([dim, 1])
x = np.concatenate((np.ones([12 * 471, 1]), x), axis=1).astype(float)
learning_rate = 100  # 学习率
iter_time = 1000  # 迭代次数
adagrad = np.zeros([dim, 1])
eps = 0.0000000001

# 均方根误差函数RMSE
for t in range(iter_time):
    loss = np.sqrt(np.sum(np.power(np.dot(x, w) - y, 2)) / (471 * 12))  # 计算误差，按照公式即可
    '''if t % 100 == 0:
        print(str(t) + ":" + str(loss))'''
    gradient = 2 * np.dot(x.transpose(), np.dot(x, w) - y)  
    adagrad += gradient ** 2
    w = w - learning_rate * gradient / np.sqrt(adagrad + eps)
np.save('weight.npy', w)  # save保存成二进制文件

其中，loss function 我们选择均方根误差
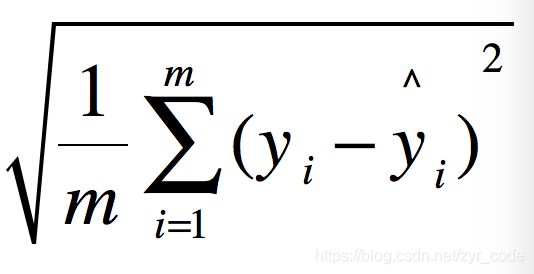至于学习率，最简单的办法就是固定学习率，每次迭代的学习率都相同，但这样效果也会很差，良好的学习率应随迭代次数依次减少，所以我们使用自适应学习率的adagrad算法，即每次学习率都等于其除以之前所有的梯度平方和再开根号，即下图所示的公式:
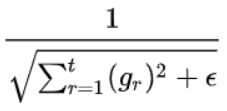gradient就是一个对Loss函数进行每个参数的偏微分而得到的矩阵。

Step5：载入验证集进行验证

# 用训练集交叉验证？
w = np.load('weight.npy')
x_validation = np.concatenate((np.ones([1131, 1]), x_validation), axis=1).astype(float)
loss = np.sqrt(np.sum(np.power(np.dot(x_validation, w) - y_validation, 2)) / 1131)
# print(loss)
testdata = pd.read_csv('./test.csv', header=None, encoding='big5')
testdata[testdata == 'NR'] = 0
test_data = testdata.iloc[:, 2:]
test_data = test_data.to_numpy()  # 这里有个bug
test_x = np.empty([240, 18 * 9], dtype=float)
for i in range(240):
    test_x[i, :] = test_data[i * 18:(i + 1) * 18, :].reshape(1, -1)

# normalize
for i in range(len(test_x)):
    for j in range(len(test_x[0])):
        if std_x[j] != 0:
            test_x[i][j] = (test_x[i][j] - mean_x[j]) / std_x[j]
test_x = np.concatenate((np.ones([240, 1]), test_x), axis=1).astype(float)

这里在处理testdata[testdata == ‘NR’] = 0时报了一个warnning，根据错误提示将testdata先筛选在iloc之后就可以了，但是很奇怪在上面处理数据的时候并没有出错。

Step 6：预测testdata

数据处理的步骤和之前一样

w = np.load('./weight.npy')
ans_y = np.dot(test_x, w)

# 将预测结果写入文件当中
with open('submit.csv', mode='w', newline='') as submit_file:
    csv_writer = csv.writer(submit_file)
    header = ['id', 'value']
    # print(header)
    csv_writer.writerow(header)
    for i in range(240):
        write_row = ['id_' + str(i), ans_y[i][0]]
        csv_writer.writerow(write_row)
    # print(write_row)

代码写到这里基本就结束了。

Step7：总结

大约花了一天的时间，终于将第一次作业代码运行出来并且能看懂，这是第一次敲机器学习相关的代码，在过程中很多基本方法都不知道用法导致每一个方法都要去查文档，这样的速度慢了很多。相信在以后的学习中效率会越来越高。
整个思路参考：https://mrsuncodes.github.io/2020/03/15/%E6%9D%8E%E5%AE%8F%E6%AF%85%E6%9C%BA%E5%99%A8%E5%AD%A6%E4%B9%A0-%E7%AC%AC%E4%B8%80%E8%AF%BE%E4%BD%9C%E4%B8%9A/#more.
感谢大佬的热心分享。