概率论Probability①
重视 intuition!
当前两大学派:
- 贝叶斯学派
- 频率学派
两者区别在于对参数的看法(待补充)
De Morgan’s laws:

样本空间(sample space):
- 基本概念
试验产生的所有结果形成样本空间Ω
样本空间的试验结果可能是有限,也可能是无限
讨论的概念模型只涉及一个试验,所系连续抛三次硬币只能作为一次试验 - 选择方法
试验结果互斥、完整
根据研究兴趣选择
细节足够,避免繁琐
离散(序贯模型):树形图中试验结果在叶子节点
连续: unit 1 × 1(注意样本空间的归一化)
事件(Event)
样本空间的子集,即某些试验结果的集合。
概率公理(Axioms)
非负性(Nonnegativity) P ( A ) ≥ 1 P(A) ≥ 1 P(A)≥1
归一化(Normalization) P ( Ω ) = 1 P(\Omega) = 1 P(Ω)=1
(Finite)可加性(Additivity) A ∩ B = ∅ , P ( A ∪ B ) = P ( A ) + P ( B ) A∩B=∅, P(A∪B) = P(A) + P(B) A∩B=∅,P(A∪B)=P(A)+P(B)
将可加性推广到可数可加性:
若 A 1 , A 2 , . . . A1, A2,... A1,A2,...是两两互不相容的事件,则有
P ( A 1 ∪ A 2 ∪ . . . ) = P ( A 1 ) + P ( A 2 ) + . . . P(A1∪A2∪...) = P(A1)+P(A2)+... P(A1∪A2∪...)=P(A1)+P(A2)+...
由概率公理可推导出概率律的性质:
P ( ∅ ) = 0 P(∅) = 0 P(∅)=0
1 = P ( Ω ) = P ( Ω ∩ ∅ ) = P ( Ω ) + P ( ∅ ) = 1 + P ( ∅ ) 1= P(\Omega)=P(\Omega ∩ ∅ ) = P(\Omega) + P(∅) = 1 + P(∅) 1=P(Ω)=P(Ω∩∅)=P(Ω)+P(∅)=1+P(∅)
P ( A ) ≤ 1 P(A)≤1 P(A)≤1
P ( A ) = 1 − P ( A c ) P(A) = 1 - P(A^c) P(A)=1−P(Ac)
P ( A ) + P ( A c ) = 1 P(A)+P(A^c)=1 P(A)+P(Ac)=1
1 = P ( Ω ) = P ( A ∪ A c ) = P ( A ) + P ( A c ) 1= P(\Omega) = P(A∪A^c) = P(A) +P(A^c) 1=P(Ω)=P(A∪Ac)=P(A)+P(Ac)
I f If If A ⊂ B , t h e n A \subset B, then A⊂B,then P ( A ) ≤ P ( B ) P(A)≤P(B) P(A)≤P(B)
P ( A ∪ B ) = P ( A ) + P ( B ) − P ( A ∩ B ) P(A∪B) = P(A)+P(B)-P(A∩B) P(A∪B)=P(A)+P(B)−P(A∩B) Note: Not necessarily disjoint
P ( A ∪ B ) ≤ P ( A ) + P ( B ) P(A∪B) ≤P(A)+P(B) P(A∪B)≤P(A)+P(B) union bound
推广可得
P ( ⋃ i A i ) ≤ ∑ i P ( A i ) {\displaystyle P(\bigcup _{i}A_{i})\leq \sum _{i}P(A_{i})} P(i⋃Ai)≤i∑P(Ai)
https://zh.wikipedia.org/wiki/布尔不等式
全部事件的概率不大于单个事件的概率总和
P ( A ∪ B ∪ C ) = P ( A ) + P ( A c ∩ B ) + P ( A c ∩ B c ∩ C ) P(A∪B∪C) = P(A)+P(A^c∩B)+P(A^c∩B^c∩C) P(A∪B∪C)=P(A)+P(Ac∩B)+P(Ac∩Bc∩C)

离散模型(discrete/finite example)
由n个(有限个 等可能)的结果组成。事件的概率可由组成这个事件的试验结果的概率决定。
P ( s 1 , s 2 , … … , s n ) = P ( s 1 ) + P ( s 2 ) + … … + P ( s n ) P({s_{1}, s_{2},……, s_{n}}) = P(s_{1}) + P(s_{2}) +……+P(s_{n}) P(s1,s2,……,sn)=P(s1)+P(s2)+……+P(sn)
古典概型(离散均匀模型):
P ( A ) = 含 于 事 件 A 的 试 验 结 果 数 n P(A) = \frac{含于事件A的试验结果数}{n} P(A)=n含于事件A的试验结果数
小技巧:
- 不要失去常识,也不过分依赖
- 情景证明(story proof):最简单的情形验证simplicial non-attributed case
连续模型
由无限个 等可能的结果组成。
P r o b a b i l i t y = A r e a Probability = Area Probability=Area
利用可加性公理,单点组成的事件的概率必定为0。用长度刻画概率律的合法性取决于单位区间是一个不可数无限集,否则单点的概率为零,会导致[0, 1]的概率为0的结论,与归一化矛盾。
几何概率模型(连续均匀模型):
设样本空间 Ω ⊂ R r \Omega\subset R^r Ω⊂Rr的体积 m ( Ω ) m(\Omega) m(Ω)是正数,且 Ω \Omega Ω中的每个试验结果发生的可能性相同,对于事件 A ⊂ Ω A\subset \Omega A⊂Ω,其发生的概率为
P ( A ) = m ( A ) m ( Ω ) P(A)=\frac{m(A)}{m(\Omega)} P(A)=m(Ω)m(A)
贝特朗悖论 (Bertrand paradox)
考虑一个内接于圆的等边三角形。若随机选圆上的弦,则此弦的长度比三角形的边( 3 \sqrt3 3)较长的机率?
用来举例说明,若产生随机变数的“机制”或“方法”没有清楚定义好的话,机率也将无法得到良好的定义。
-
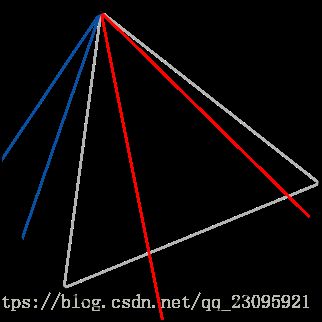
随机端点
通过三角形任意一个顶点做圆的切线,因为等边三角形内角为60°,所以左边右边的角都是60°。由该顶点做一条弦,弦的另一端在圆上任意一点。由图可知弦与切线成60°角和120°角之间的时候弦长度大于三角形边长。所以概率为 1 3 \frac{1}{3} 31.
-
随机中点
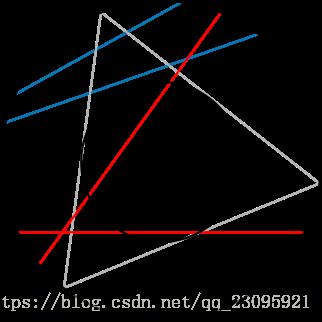
选择圆内的任意一点,并画出以此点为中点的弦。可观察到,若选择的点落在半径只有大圆的半径的二分之一的同心圆之内,则弦的长度会比三角形的边较长。小圆的面积是大圆的四分之一,因此随机的弦会比三角形的边较长的机率为 1 4 \frac{1}{4} 41。 -
随机半径
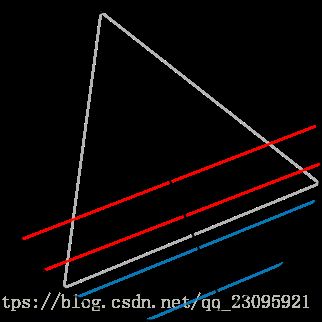
选择一个圆的半径和半径上的一点,再画出通过此点并垂直半径的弦。可观察到,若选择的点比三角形和半径相交的点要接近圆的中心,则弦的长度会比三角形的边较长。三角形的边会平分半径,因此随机的弦会比三角形的边较长的机率为 1 2 \frac{1}{2} 21。
Q1. 为什么概率要分配到事件上,每个试验结果也会有概率吗?
https://en.wikipedia.org/wiki/Outcome_(probability)
Since individual outcomes may be of little practical interest, or because there may be prohibitively (even infinitely) many of them, outcomes are grouped into sets of outcomes that satisfy some condition, which are called “events.” The collection of all such events is a sigma-algebra.
Typically, when the sample space is finite, any subset of the sample space is an event (i.e. all elements of the power set of the sample space are defined as events). However, this approach does not work well in cases where the sample space is uncountably infinite (most notably when the outcome must be some real number). So, when defining a probability space it is possible, and often necessary, to exclude certain subsets of the sample space from being events.
Outcomes may occur with probabilities that are between zero and one (inclusively). In a discrete probability distribution whose sample space is finite, each outcome is assigned a particular probability. In contrast, in a continuous distribution, individual outcomes all have zero probability, and non-zero probabilities can only be assigned to ranges of outcomes.
…通常来说,当样本空间是有限的,其中所有子集均为事件。(例:样本空间的幂集的所有元素都被定义为事件)。 然而这种方法不适用于样本空间不可测且无限的情况(最明显的是当结果必须是某个实数时)。
…在连续分布中,个体结果都具有零概率,而非零概率只能分配给试验结果的范围。
https://en.wikipedia.org/wiki/Event_(probability_theory)
Defining all subsets of the sample space as events works well when there are only finitely many outcomes, but gives rise to problems when the sample space is infinite. For many standard probability distributions, such as the normal distribution, the sample space is the set of real numbers or some subset of the real numbers. Attempts to define probabilities for all subsets of the real numbers run into difficulties when one considers ‘badly behaved’ sets, such as those that are nonmeasurable. Hence, it is necessary to restrict attention to a more limited family of subsets. For the standard tools of probability theory, such as joint and conditional probabilities, to work, it is necessary to use a σ-algebra, that is, a family closed under complementation and countable unions of its members. The most natural choice is the Borel measurable set derived from unions and intersections of intervals. However, the larger class of Lebesgue measurable sets proves more useful in practice.
In the general measure-theoretic description of probability spaces, an event may be defined as an element of a selected σ-algebra of subsets of the sample space. Under this definition, any subset of the sample space that is not an element of the σ-algebra is not an event, and does not have a probability. With a reasonable specification of the probability space, however, all events of interest are elements of the σ-algebra.
当考虑“行为不良”集合(例如那些不可测量的集合)时,尝试定义实数的所有子集的概率会遇到困难。因此,有必要将注意力限制在更有限的子集中。
…
在概率空间的一般测量理论描述中,一个事件可以被定义为一种在样本空间中选定的σ-代数的元素的子集。在此定义下,任何不是σ-代数元素的样本空间的子集都不是事件,并且没有概率。 然而通过合理规定的样本空间中所有我们感兴趣的事件都是都是σ-代数的元素。
事实上,如果当概率分配给具体的试验结果而不是事件,就可能遇到问题。在无限不可测的集合中,
Q2. 任何奇怪的集合也都有概率吗?
不是。考虑不可测集。
随机抽样与随机分配
计数法(没学懂QAQ)
二项式定理与扩展
参考:https://www.coursera.org/learn/discrete-mathematics-ch/lecture/LDZx3/er-xiang-shi-ding-li-duo-xiang-shi-ding-li
k元子集计数
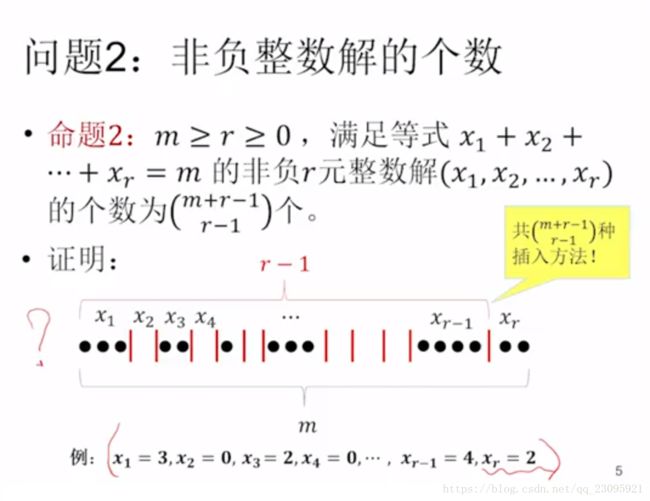
已知集合 X X X的大小为 n n n(即 ∣ X ∣ = n |X|=n ∣X∣=n), n ≥ k ≥ 0 n≥k≥0 n≥k≥0, X X X的所有子集中正好有 k k k个元素的子集一共有多少?
( X k ) = { { a , b } , { a , c } , { b , c } } , ∣ ( X k ) ∣ = 3 \begin{pmatrix}X\\k\end{pmatrix}= \begin{Bmatrix} \begin{Bmatrix}{a,b}\end{Bmatrix}, \begin{Bmatrix}{a,c}\end{Bmatrix}, \begin{Bmatrix}{b,c}\end{Bmatrix} \end{Bmatrix} , \begin{vmatrix} \begin{pmatrix}X\\k\end{pmatrix} \end{vmatrix} =3 (Xk)={ { a,b},{ a,c},{ b,c}},∣∣∣∣(Xk)∣∣∣∣=3
所有K元子集个数为:
∣ ( X k ) ∣ = n ( n − 1 ) ( n − 2 ) . . . ( n − k + 1 ) k ( k − 1 ) . . . 2 ⋅ 1 \begin{vmatrix} \begin{pmatrix}X\\k\end{pmatrix} \end{vmatrix} = \frac{n(n-1)(n-2)...(n-k+1)}{k(k-1)...2·1} ∣∣∣∣(Xk)∣∣∣∣=k(k−1)...2⋅1n(n−1)(n−2)...(n−k+1)
- 证明:
从 X X X中取 k k k元不重复有序组,共有 n ( n − 1 ) ( n − 2 ) . . . ( n − k + 1 ) n(n-1)(n-2)...(n-k+1) n(n−1)(n−2)...(n−k+1)种方法;
从任意1个 X X X的 k k k元子集出发,可以得到 k ! k! k!个不同的 k k k元有序组。
左右相等,即:
n ( n − 1 ) ( n − 2 ) . . . ( n − k + 1 ) = k ! ⋅ ∣ ( X k ) ∣ n(n-1)(n-2)...(n-k+1)=k!·\begin{vmatrix} \begin{pmatrix}X\\k\end{pmatrix} \end{vmatrix} n(n−1)(n−2)...(n−k+1)=k!⋅∣∣∣∣(Xk)∣∣∣∣
上下同乘 ( n − k ) ⋅ . . . ⋅ 1 (n-k)·...·1 (n−k)⋅...⋅1
∣ ( X k ) ∣ = n ( n − 1 ) ( n − 2 ) . . . ( n − k + 1 ) k ( k − 1 ) . . . 2 ⋅ 1 = n ! k ! ( n − k ) ! \begin{vmatrix} \begin{pmatrix}X\\k\end{pmatrix} \end{vmatrix} = \frac{n(n-1)(n-2)...(n-k+1)}{k(k-1)...2·1} = \frac{n!}{k!(n-k)!} ∣∣∣∣(Xk)∣∣∣∣=k(k−1)...2⋅1n(n−1)(n−2)...(n−k+1)=k!(n−k)!n!
基本性质
- ( n k ) = ( n n − k ) \begin{pmatrix}n\\k\end{pmatrix} = \begin{pmatrix}n\\n-k\end{pmatrix} (nk)=(nn−k)
- ( n k ) = ( n − 1 k − 1 ) + ( n − 1 k ) \begin{pmatrix}n\\k\end{pmatrix} = \begin{pmatrix}n-1\\k-1\end{pmatrix}+ \begin{pmatrix}n-1\\k\end{pmatrix} (nk)=(n−1k−1)+(n−1k)

- Vandermonde’s identity
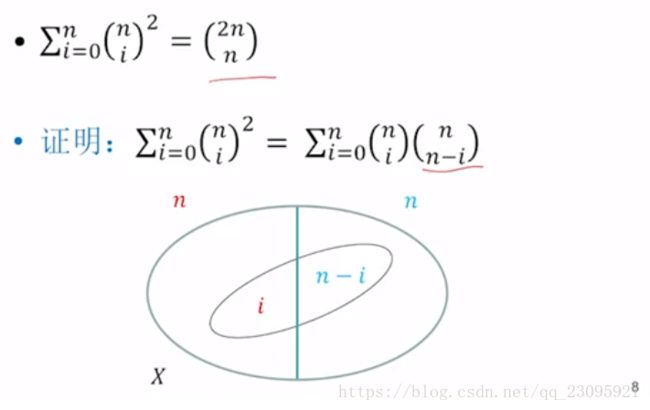
∑ i = 0 k ( n i ) ( m k − i ) = ( n + m k ) {\displaystyle \sum _{i=0}^{k}{\binom {n}{i}}{\binom {m}{k-i}}={\binom {n+m}{k}}} i=0∑k(in)(k−im)=(kn+m)
直观:从(n+m)两个箱子中选k个球有 ( n + m k ) \binom {n+m}{k} (kn+m)种选法。从n中选i个球,则从m中需选出(k-i)个球,考虑所有的情况 i = 0 , 1 , … , k i = 0 , 1 , … , k {\displaystyle i=0,1,\ldots ,k} {\displaystyle i=0,1,\ldots ,k} i=0,1,…,ki=0,1,…,k,即 ∑ i = 0 k ( n i ) ( m k − i ) {\displaystyle \sum _{i=0}^{k}{\binom {n}{i}}{\binom {m}{k-i}}} i=0∑k(in)(k−im)
当m=n的特殊情况: