JAVA 数据结构-06 (3) 栈结构的应用 前 中 后缀三种表达式 中缀表达式转后缀表达式 逆波兰计算器实现和算法思路
JAVA 数据结构学习-05.栈
JAVA 数据结构-06 (1)栈的基本数据结构实现(数组实现,链表实现)
JAVA 数据结构-06 (2) 栈结构的应用 简易计算表达式的计算(中缀表达式)
2. 栈结构的应用(表达式与计算器)
2.2 前 中 后缀三种表达式
- 前缀表达式(波兰表达式)
- 运算符位于操作数之前
- 举例:(3+4)*5-6的前缀表达式就是 - * + 3 4 5 6
- 计算机求值的流程:从右至左进行扫描,遇到数字,将数字压入堆栈,遇到运算符,弹出栈顶两个数,用运算符进行计算,并将结果压入栈,重复操作直到表达式最左端,最后得出的结果就是表达式的结果.
- 中缀表达式
- 最常见的运算表达式 (3+4)*5-6
- 对于计算机并不好操作( 需要判断相邻运算符的优先级 ),因此在计算结果时,往往会将中缀表达式转成其他表达式来操作(一般转换成后缀表达式)
- 后缀表达式(逆波兰表达式)
- 运算符位于操作数之后
- 举例:(3+4)*5-6的后表达式就是: 3 4 + 5 * 6 -
- 计算机求值流程:从左至右扫描表达式,遇到数字时,压入堆栈,遇到运算符时,弹出栈顶的两个元素进行计算,将结果入栈,重复上述过程知道表达式的最右端,最后的结果就是表B达式的结果
- 注意:此时栈顶的两个元素与前缀表达式是相反的,当遇到减和除时,需要使用栈顶次元素减/除栈顶元素
2.2.1 中缀表达式转后缀表达式
从上面的表达式介绍可以看出,后缀表达式的计算机求值流程要简单于中缀表达式(不涉及运算符优先级的操作),因此往往将中缀表示转换为后缀表达式进行计算.
实现思路:
- 初始化两个栈:运算符栈s1和存储中间结果的栈s2;
- 从左到右扫描中缀表达式;
- 遇到操作数时,将其压入s2;
- 遇到运算符时,比较其与s1栈顶运算符的优先级:分一下几种情况
- 如果s1为空,或栈顶运算符为左括号’(’,则直接将此运算符入栈;
- 否则,若优先级比栈顶的运算符高,也将运算符压入s1;
- 否则,将s1栈顶的运算符弹出并压入到s2中,再次转到4.1与s1中新的栈顶运算符进行比较;
- 遇到括号时:分以下情况
- 如果时左括号’(’,则直接压入s1
- 如果是右括号’)’,则依次弹出s1栈顶的运算符,并压入s2,直到遇到左括号为止,此时将这一对括号丢弃
- 重复步骤2-5,直到表达式遍历完成
- 将s1中剩余的运算符依次弹出并压入s2
- 依次弹出s2中的元素并输出,结果的逆序即为中缀表达式对应的后缀表达式.
举例:
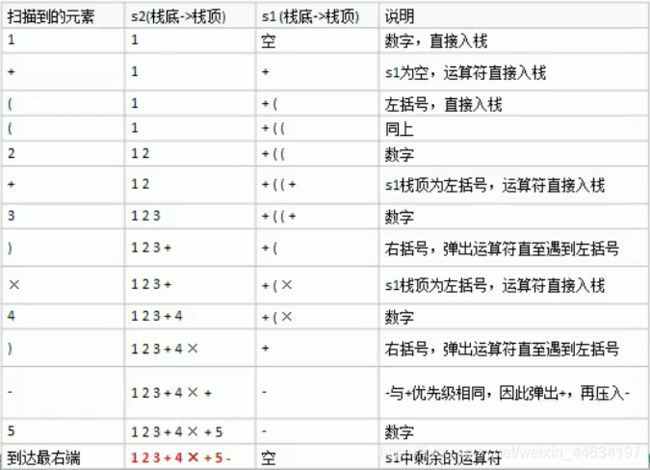
将1+((2+3)*4)-5 转换为后缀表达式的步骤:
代码实现: (递归实现)
public class PolandNotation {
public static void main(String args[]){
//将中缀字符串表达式转换为list存储,并且区分多位数字
String expression ="1+((2+3)*4)-5";
List<String> list = toList(expression); //list: [15, +, (, (, 2, +, 3, ), *, 4, ), -, 5]
//将中缀表达式list转换后缀表达式的list
List<String> tosuffixList = tosuffixList(list);
System.out.println(tosuffixList);//tosuffixList:[1, 2, 3, +, 4, *, +, 5, -]
}
public static List<String> tosuffixList(List<String> expressionList){
//1.初始化两个栈:运算符栈s1和存储中间结果的栈s2;
Stack<String> s1 = new Stack<>();
Stack<String> s2 = new Stack<>();
//2.从左到右扫描中缀表达式;
expressionList.forEach(item ->{
//3.遇到操作数时,将其压入s2; 使用正则表达式匹配多位数字
if(item.matches("\\d+")){
s2.push(item);
}else if(isOper1(item)){
//4.遇到运算符时,比较其与s1栈顶运算符的优先级:
addOper1(s1,s2,item);
}else if(isOper2(item)){
//5. 遇到括号时:
addOper2(s1,s2,item);
}
});
//6. 重复步骤2-5,直到表达式遍历完成
//7. 将s1中剩余的运算符依次弹出并压入s2
while (!s1.isEmpty()){
s2.push(s1.pop());
}
//8. 依次弹出s2中的元素并输出,结果的逆序即为中缀表达式对应的后缀表达式.
ArrayList<String> suffixList = new ArrayList<>();
while (!s2.isEmpty()){
suffixList.add(s2.pop());
}
Collections.reverse(suffixList);
return suffixList;
}
//添加运算符
public static void addOper1(Stack<String> s1,Stack<String> s2,String item){
if(s1.isEmpty() || "(".equals(s1.peek())){
//4.1 如果s1为空,或栈顶运算符为左括号'(',则直接将此运算符入栈;
s1.push(item);
}else if(priority(item)>priority(s1.peek())){
//4.2 否则,若优先级比栈顶的运算符高,也将运算符压入s1;
s1.push(item);
}else {
//4.3 否则,将s1栈顶的运算符弹出并压入到s2中,再次转到4.1与s1中新的栈顶运算符进行比较;
s2.push(s1.pop());
addOper1(s1,s2,item);
}
}
//添加括号
public static void addOper2(Stack<String> s1,Stack<String> s2,String item){
if("(".equals(item)){
//5.1 如果时左括号'(',则直接压入s1
s1.push(item);
}else if(")".equals(item)){
//5.2 如果是右括号')',则依次弹出s1栈顶的运算符,并压入s2,直到遇到左括号为止,此时将这一对括号丢弃
s2.push(s1.pop());
if("(".equals(s1.peek())){
s1.pop(); //将丢弃左右括号
return;
}
addOper2( s1, s2,item);
}
}
//判断是否是操作符
public static boolean isOper1(String value){
return "+".equals(value) || "-".equals(value) || "*".equals(value) || "/".equals(value);
}
//判断是否是括号
public static boolean isOper2(String value){
return "(".equals(value) || ")".equals(value);
}
//返回操作符的优先级 */优先级高于+-
public static int priority(String value){
if("*".equals(value) || "/".equals(value)){
return 1;
}
if("+".equals(value) || "-".equals(value)){
return 0;
}
return -1;
}
}
2.3 逆波兰计算器的实现
目标:
- 输入一个逆波兰表达式(后缀),使用栈(Stack),计算其结果
- 支持小括号和多位整数运算
思路分析:
-
计算只需要一个数栈
-
计算机求值流程:从左至右扫描表达式,遇到数字时,压入堆栈,遇到运算符时,弹出栈顶的两个元素进行计算,将结果入栈,重复上述过程知道表达式的最右端,最后的结果就是表B达式的结果
-
注意:此时栈顶的两个元素与前缀表达式是相反的,当遇到减和除时,需要使用栈顶次元素减/除栈顶元素
代码实现:
public class PolandNotation {
public static void main(String args[]){
//先定义一个逆波兰表达式
//为了方便取值,逆波兰表达式使用空格进行运算符和数字(多位)的分割
//中缀表达式 (30 + 4) * 5 -6 -> 30 4 + 5 * 6 -
String suffixExpression = "30 4 + 5 * 6 -";
int result = calculate(getListString(suffixExpression));
System.out.println("计算的结果是:"+result);
}
//将表达式转化成list数组,方便计算和遍历
public static List<String> getListString(String suffixExpression){
String[] split = suffixExpression.split(" ");
List<String> list = Arrays.asList(split);
return list;
}
public static int calculate(List<String> list){
Stack<String> stack = new Stack<String>();
for (String item:list){
int res = 0;
//使用正则表达式匹配多位数字
if(item.matches("\\d+")){
//是数字,压入栈中
stack.push(item);
}else{
//取出两个元素进行计算
int num1 = Integer.parseInt(stack.pop());
int num2 = Integer.parseInt(stack.pop());
if("+".equals(item)){
res = num1 + num2;
}else if("-".equals(item)){
//逆波兰计算时,减法和除法的先后位置与前缀表达式表达式相反 (次元素-栈顶元素)
res = num2 - num1;
}else if("*".equals(item)){
res = num1 * num2;
}else if("/".equals(item)){
res = num2 / num1;
}
//将结果压入栈中
stack.push(res+"");
}
}
//循环结束后,栈顶元素就是计算的最终结果
return Integer.parseInt(stack.pop());
}
}
2.4 完成的中缀转后缀表达式 计算器求值
代码实现:
import java.util.*;
public class PolandNotation {
public static void main(String args[]){
//将中缀字符串表达式转换为list存储,并且区分多位数字
String expression ="1+((2+3)*4)-5";
List<String> list = toList(expression); //list: [15, +, (, (, 2, +, 3, ), *, 4, ), -, 5]
//将中缀表达式list转换后缀表达式的list
List<String> tosuffixList = tosuffixList(list);
System.out.println(tosuffixList);//tosuffixList:[1, 2, 3, +, 4, *, +, 5, -]
int result = calculate(tosuffixList);
System.out.println("计算的结果是:"+result);//计算的结果是:16
}
public static List<String> tosuffixList(List<String> expressionList){
//1.初始化两个栈:运算符栈s1和存储中间结果的栈s2;
Stack<String> s1 = new Stack<>();
Stack<String> s2 = new Stack<>();
//2.从左到右扫描中缀表达式;
expressionList.forEach(item ->{
//3.遇到操作数时,将其压入s2; 使用正则表达式匹配多位数字
if(item.matches("\\d+")){
s2.push(item);
}else if(isOper1(item)){
//4.遇到运算符时,比较其与s1栈顶运算符的优先级:
addOper1(s1,s2,item);
}else if(isOper2(item)){
//5. 遇到括号时:
addOper2(s1,s2,item);
}
});
//6. 重复步骤2-5,直到表达式遍历完成
//7. 将s1中剩余的运算符依次弹出并压入s2
while (!s1.isEmpty()){
s2.push(s1.pop());
}
//8. 依次弹出s2中的元素并输出,结果的逆序即为中缀表达式对应的后缀表达式.
ArrayList<String> suffixList = new ArrayList<>();
while (!s2.isEmpty()){
suffixList.add(s2.pop());
}
Collections.reverse(suffixList);
return suffixList;
}
//添加运算符
public static void addOper1(Stack<String> s1,Stack<String> s2,String item){
if(s1.isEmpty() || "(".equals(s1.peek())){
//4.1 如果s1为空,或栈顶运算符为左括号'(',则直接将此运算符入栈;
s1.push(item);
}else if(priority(item)>priority(s1.peek())){
//4.2 否则,若优先级比栈顶的运算符高,也将运算符压入s1;
s1.push(item);
}else {
//4.3 否则,将s1栈顶的运算符弹出并压入到s2中,再次转到4.1与s1中新的栈顶运算符进行比较;
s2.push(s1.pop());
addOper1(s1,s2,item);
}
}
//添加括号
public static void addOper2(Stack<String> s1,Stack<String> s2,String item){
if("(".equals(item)){
//5.1 如果时左括号'(',则直接压入s1
s1.push(item);
}else if(")".equals(item)){
//5.2 如果是右括号')',则依次弹出s1栈顶的运算符,并压入s2,直到遇到左括号为止,此时将这一对括号丢弃
s2.push(s1.pop());
if("(".equals(s1.peek())){
s1.pop(); //将丢弃左右括号
return;
}
addOper2( s1, s2,item);
}
}
//判断是否是操作符
public static boolean isOper1(String value){
return "+".equals(value) || "-".equals(value) || "*".equals(value) || "/".equals(value);
}
//判断是否是括号
public static boolean isOper2(String value){
return "(".equals(value) || ")".equals(value);
}
//返回操作符的优先级 */优先级高于+-
public static int priority(String value){
if("*".equals(value) || "/".equals(value)){
return 1;
}
if("+".equals(value) || "-".equals(value)){
return 0;
}
return -1;
}
//将中缀字符串表达式转换为list存储,并且区分多位数字
public static List<String> toList(String string){
ArrayList<String> list = new ArrayList<>();
int index = 0;
char ch =' ';
String number ="";
while (index <= string.length()-1){
ch = string.charAt(index);
if(ch<48 || ch>57){
//此时为非数字,直接添加到list中
list.add(ch+"");
index++;
}else {
//此时为数字,需要判断是否是多位数字
number ="";
while (index <= string.length()-1 &&string.charAt(index)>=48 && string.charAt(index)<=57){
number+=string.charAt(index);
index++;
}
list.add(number);
}
}
return list;
}
//将表达式转化成list数组,方便计算和遍历
public static List<String> getListString(String suffixExpression){
String[] split = suffixExpression.split(" ");
List<String> list = Arrays.asList(split);
return list;
}
public static int calculate(List<String> list){
Stack<String> stack = new Stack<String>();
for (String item:list){
int res = 0;
//使用正则表达式匹配多位数字
if(item.matches("\\d+")){
//是数字,压入栈中
stack.push(item);
}else{
//取出两个元素进行计算
int num1 = Integer.parseInt(stack.pop());
int num2 = Integer.parseInt(stack.pop());
if("+".equals(item)){
res = num1 + num2;
}else if("-".equals(item)){
//逆波兰计算时,减法和除法的先后位置与前缀表达式表达式相反 (次元素-栈顶元素)
res = num2 - num1;
}else if("*".equals(item)){
res = num1 * num2;
}else if("/".equals(item)){
res = num2 / num1;
}
//将结果压入栈中
stack.push(res+"");
}
}
//循环结束后,栈顶元素就是计算的最终结果
return Integer.parseInt(stack.pop());
}
}