数据分析入门(学术前沿趋势分析)Task5-作者信息关联
Task4链接——数据分析入门(学术前沿趋势分析)Task4-论文种类分类
目录
Ⅰ、主要内容纲要
Ⅱ、数据处理思路
Ⅲ、代码实现
Ⅳ、参考资料
Ⅰ、主要内容纲要
- 主题:对作者间的关系进行建模并分析,统计关联最大的作者关系
- 内容: 构建作者关系图
- 数据集:arXiv
Ⅱ、数据处理思路
-
处理步骤
将作者列表进行处理,并完成统计。具体步骤如下:
1)将论文第一作者与其他作者(非第一作者)关系构建图结构;
2)使用图算法相关操作统计图中某作者与其他作者的联系。
-
社交网络
社交网络是一种网络,属于图的一种类型。图是一种重要的结构,是离散数学、数据结构、运筹学等学科的重要内容,广泛应用于现实生活中(如交通规划、网络规划、流程规划等)。python可以利用networkx库实现图的算法操作。
networkx参考资料:
NetworkX(图论)的基本操作
NetworkX官方文档
NetworkX中文文档
图结构及相关算法资料:
图像处理十大经典算法
课程-数据结构-王道论坛
课程-算法设计与分析(北航)-中国大学MOOC
Ⅲ、代码实现
导入数据:
import json #读取数据,我们的数据为json格式的
import pandas as pd #数据处理,数据分析
import matplotlib.pyplot as plt #画图工具
# 导入数据
data = [] #初始化
#使用with语句优势:1.自动关闭文件句柄;2.自动显示(处理)文件读取数据异常
with open("file location/arxiv-metadata-oai-snapshot.json", 'r') as f:
for idx, line in enumerate(f):
d = json.loads(line)
d = {'authors_parsed': d['authors_parsed']}
data.append(d)
data = pd.DataFrame(data) #将list变为dataframe格式,方便使用pandas进行分析构建作者关系的无向图并绘制:
# 创建作者链接的无向图
import networkx as nx
# 创建无向图
G = nx.Graph()
# 用一百篇论文进行构建
for row in data.iloc[:100].itertuples():
authors = row[1]
authors = [' '.join(x[:-1]) for x in authors]
# 第一个作者 与 其他作者链接
for author in authors[1:]:
G.add_edge(authors[0],author) # 添加节点2,3并链接23节点
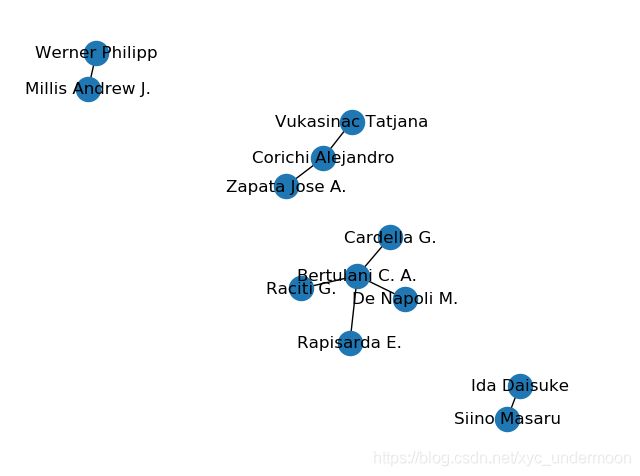
# 将作者关系图进行绘制
nx.draw(G, with_labels=True)(这里用一百篇论文作者进行画图,人数众多,画出的图不清晰,因此也截取了一张局部图)
查看某两作者之间的最短关系路径:
# 作者之间关系的距离
try:
print(nx.dijkstra_path(G, 'Shu Zhan', 'Zhu Shi-Lin'))
except:
print('No path')out: ['Shu Zhan', 'Chen Xiao-Lin', 'Chen Chong', 'Zhu Shi-Lin']
可以看出, Shu Zhan到 Zhu Shi-Lin的关系路径是Shu Zhan→Chen Xiao-Lin→Chen Chong→Zhu Shi-Lin,说明Shu Zhan与 Zhu Shi-Lin并没有直接关系,但可以通过中间两人关系的连接相互联系。
这里使用Dijkstra算法计算距离, Dijkstra算法用来计算无环图中某结点到其他节点之间的最短距离(单源最短路径)。
简单叙述一下Dijkstra算法的基本思想:要找从某点到其他结点的最短距离,首先找到该点到其直接可达结点(就是从该点可以直接到达的结点)的最短距离,然后从这两点找寻直接可达结点中距离最短的结点,继续这样反复寻找,直到遍历完整个极大连通子图。Dijkstra算法图示过程如下图所示:
Dijkstra算法参考资料:
最短路径 | 深入浅出Dijkstra算法(一)
课程-算法设计与分析(北航)-中国大学MOOC
查看关系图中的极大连通子图个数:
# 计算论文关系中有多少个联通子图
print(len(nx.communicability(G)))可以得到这100个数据所构建的图中极大联通子图有169个。
选择最大联通子图进行绘制,折线图为子图节点度值。
degree_sequence = sorted([d for n, d in G.degree()])
dmax = max(degree_sequence)
plt.loglog(degree_sequence, "b-", marker="o") # 画双对数坐标
plt.title("Degree rank plot")
plt.ylabel("degree")
plt.xlabel("rank")
# draw graph in inset
plt.axes([0.45, 0.45, 0.45, 0.45])
Gcc = G.subgraph(sorted(nx.connected_components(G), key=len, reverse=True)[0])
pos = nx.spring_layout(Gcc)
plt.axis("off")
nx.draw_networkx_nodes(Gcc, pos, node_size=20)
nx.draw_networkx_edges(Gcc, pos, alpha=0.4)
plt.show()
Ⅳ、参考资料
Datawhale数据分析训练营学习手册(学术前沿趋势分析)——Task5:作者信息关联
NetworkX(图论)的基本操作
NetworkX官方文档
NetworkX中文文档
图像处理十大经典算法
课程-数据结构-王道论坛
课程-算法设计与分析(北航)-中国大学MOOC
最短路径 | 深入浅出Dijkstra算法(一)
最短路径 | 深入浅出Dijkstra算法(二)
Python中的loglog是什么意思?
matplotlib.pyplot-API