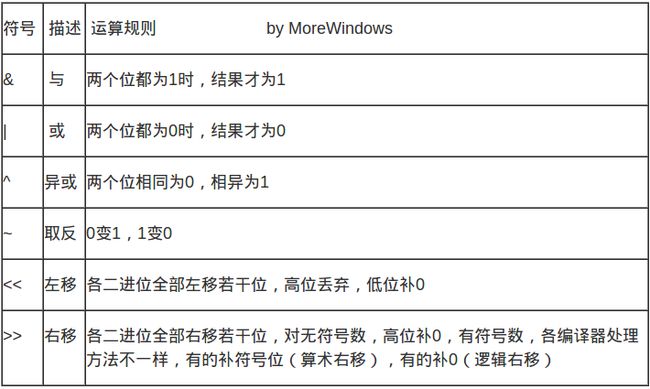
基本的位操作符有与、或、异或、取反、左移、右移这6种:
位运算示例操作
位运算示例操作
| 位运算 | 功能 | 示例 | |
|---|---|---|---|
| x >> 1 | 去掉最后一位 | 101101->10110 | |
| x << 1 | 在最后加一个0 | 101101->1011010 | |
| x << 1 | 在最后加一个1 | 101101->1011011 | |
| x\ | 1 | 把最后一位变成1 | 101100->101101 |
| x & -2 | 把最后一位变成0 | 101101->101100 | |
| x ^ 1 | 最后一位取反 | 101101->101100 | |
| x \ | (1 << (k-1)) | 把右数第k位变成1 | 101001->101101,k=3 |
| x & ~ (1 << (k-1)) | 把右数第k位变成0 | 101101->101001,k=3 | |
| x ^(1 <<(k-1)) | 右数第k位取反 | 101001->101101,k=3 | |
| x & 7 | 取末三位 | 1101101->101 | |
| x & (1 << k-1) | 取末k位 | 1101101->1101,k=5 | |
| x >> (k-1) & 1 | 取右数第k位 | 1101101->1,k=4 | |
| x \ | ((1 << k)-1) | 把末k位变成1 | 101001->101111,k=4 |
| x ^ (1 << k-1) | 末k位取反 | 101001->100110,k=4 | |
| x & (x+1) | 把右边连续的1变成0 | 100101111->100100000 | |
| x \ | (x+1) | 把右起第一个0变成1 | 100101111->100111111 |
| x \ | (x-1) | 把右边连续的0变成1 | 11011000->11011111 |
| (x ^ (x+1)) >> 1 | 取右边连续的1 | 100101111->1111 | |
| x & -x | 去掉右起第一个1的左边 | 100101000->1000 | |
| x&0x7F | 取末7位 | 100101000->101000 | |
| x& ~0x7F | 是否小于127 | 001111111 & ~0x7F->0 | |
| x & 1 | 判断奇偶 | 00000111&1->1 |
使用位运算的两点注意事项:
- 位操作只能用于整形数据,对float和double类型进行位操作会被编译器报错。
- 位操作符的运算优先级比较低,因为尽量使用括号来确保运算顺序
1. 判断一个数值是不是2的整数次方
解题思路:
2的整数次方对应的二进制的最高位上只有一个1,如:8,二进制为 1000; 4,二进制为 0100,
那么将该数字减去1再与该数字进行与运算,减去1 后得到二进制:7,二进制为 0111;3,二进制为 0011,可以看出 8&7 为0,
4&3 为0
所以,如果 n 是2的整数次方,那么 n & ( n - 1 )结果一定为0:
n 的数值要大于 0
1. public class Main {
3. public static void main(String[] args) {
4. int n = 8;
5. if ((n & (n-1)) == 0){
6. System.out.println("整数的二次方 true");
7. }else{
8. System.out.println("不是整数的二次方");
9. }
10. }
11. }
2. 使用位运算交换两个数字【不使用中间变量】
使用异或
1. public class Main {
3. public static void main(String[] args) {
4. int n = 8, m = 10;
5. n ^= m;
6. m ^= n;
7. n ^= m;
8. System.out.println(n + ", " + m);
9. }
10. }
如: a = 13, b = 6:
a的二进制为 13 = 8 + 4 + 1 = 1101(二进制)
b的二进制为 6 = 4 + 2 = 110(二进制)
- a ^= b a = 1101 ^ 110 = 1011;
- b ^= a b = 110 ^ 1011 = 1101; 即b == 13
- a ^= b a = 1011 ^ 1101 = 110; 即a == 6
其他方法,使用加减法
1. public class Main {
3. public static void main(String[] args) {
4. int n = 8, m = 10;
5. n = n + m;
6. m = n - m;
7. n = n - m;
8. System.out.println(n + ", " + m);
9. }
10. }
3. 计算在一个 32 位的整数的二进制表示中有多少个 1
循环使用x & (x-1)消去最后一位1,计算总共消去了多少次即可。
如:
13: 1101
12: 1100
相与:1100, 消去最后一位
1. public class Main {
3. public static void main(String[] args) {
4. // 计算在一个 32 位的整数的二进制表示中有多少个 1
5. int m = 13, num = 0;
6. while (true){
7. if (m == 0) break;
8. m &= (m-1);
9. num ++;
10. }
11. System.out.println(num);
12. }
14. }
4. 正数变成负数,或者负数变成正数
变换符号只需要取反后加1即可
1. public class Main {
3. public static void main(String[] args) {
4. // 计算在一个 32 位的整数的二进制表示中有多少个 1
5. int m = -13;
6. int changeM = ~m + 1;
7. System.out.println(changeM);
8. }
10. }
5. 判断一个数值的奇偶
只要根据最未位是0还是1来决定,为0就是偶数,为1就是奇数,所以只需要与 1 相与。
因此可以用if ((a & 1) == 0)代替if (a % 2 == 0)来判断a是不是偶数。
1. public class Main {
3. public static void main(String[] args) {
4. int m = -14;
6. if ((m & 1) == 1){
7. System.out.println("ji");
8. }else{
9. System.out.println("ou");
10. }
11. }
13. }
6. 乘以2 的m次方操作
乘以2的操作,即2的1次方,左移 1 位
System.out.println(10<<1);推导扩展:
乘以2的m次方
System.out.println(10<<2); // 乘以 2的2次方,相当于乘以 4 7.除以2运算(负奇数的运算不可用)
System.out.println(10>>1);8. 转换成绝对值
1. public class Main {
3. public static void main(String[] args) {
4. int n = 12;
6. System.out.println(0 >> 31); // 0
7. System.out.println(10 >> 31); // 0
8. System.out.println(-10 >> 31); // -1
10. System.out.println((n ^ (n >> 31)) - (n >> 31)); // 12
12. }
14. }
- 首先:n>>31 取得n的符号
若n为正数,n>>31等于0;若n为负数,n>>31等于-1 若n为正数 n^0-0数不变;
- 若 n 为负数 n^-1 需要计算 n 和 -1 的补码,异或后再取补码, 结果n变号并且绝对值减1,再减去-1就是绝对值
9.判断两数符号是否相同
true 表示 x和y有相同的符号, false表示x,y有相反的符号。
System.out.println((a ^ b) > 0);10. 求两个整数(int)的平均数
System.out.println((a+b) >> 1);11. 求两个整数的最大值
1. int max(int a,int b){
2. return b & ((a-b) >> 31) | a & (~(a-b) >> 31);
3. /*如果a>=b,(a-b)>>31为0,否则为-1*/
4. }
12.求两个整数的最小值
1. int min(int a,int b){
2. return a & ((a-b) >> 31) | b & (~(a-b) >> 31);
3. /*如果a>=b,(a-b)>>31为0,否则为-1*/
4. }
13. 两个整数的加法运算
使用 ^ 和 & 将两个整数相加
- 两个数异或:相当于两个数相加,而不考虑进位;
- 两个数相与,并左移一位:相当于求得进位;
13+11 = ?;
13 的二进制 1 1 0 1 -----a 13
11 的二进制 1 0 1 1 -----b 11
(a&b) <<1 -> 1 0 0 1 0 -----d 18
a^b -> 0 1 1 0 -----e 6
(d&e) <<1 -> 0 0 1 0 0 ------f 4
d^e -> 1 0 1 0 0 -----g 20
(f&g) <<1 -> 0 1 0 0 0 ------h 8
f^g -> 1 0 0 0 0 ------i 16
(h&i) <<1 -> 0 0 0 0 0 ------h 0 ---- -------- 没有进位了, 则退出循环
h^i -> 1 1 0 0 0 ------i 24
1. private static int getSum(int a, int b) {
2. if (a == 0) return b;
3. if (b == 0) return a;
4. while (b != 0) {
5. int carry = a & b; // 得到有进位的位置
6. a = a ^ b; // 直接相加,但是没有进位
7. b = carry << 1; // 得到进位
8. }
9. return a;
10. }
项目推荐:
Java微服务实战296集大型视频-谷粒商城【附代码和课件】
Java开发微服务畅购商城实战【全357集大项目】-附代码和课件
最全最详细数据结构与算法视频-【附课件和源码】
![]()