2021算法竞赛入门班第一节课枚举贪心习题
枚举贪心
题单链接
枚举常用算法:前缀和,差分数组,双指针(尺取法)。
文章目录
- 枚举贪心
- 各题题解
-
- 1. Flip Game
- 2. Subsequence
- 3.Quasi Binary
- 4.Protecting the Flowers
- 5.校门外的树
- 6.明明的随机数
- 7.[HNOI2003]激光炸弹
- 8.铺地毯
- 9.纪念品分组
- 10.回文日期
- 11.拼数
- 12.毒瘤xor
- 13.字符串
- 14.数学考试
- 15.「土」秘法地震
- 16.丢手绢
各题题解
1. Flip Game
题目链接
题意描述:给定一个4*4的矩阵,用w代表白色,b代表黑色。你可以做如下操作,选择任意行任意列的一个元素,将其颜色反转,同时改元素的上、下、左、右的元素也会反转。即b -> w , w -> b。求最少操作几次,即可使该矩阵的元素颜色全为白色,或者全为黑色。
解题思路: 开始我以为只需要根据第一行灯的状态,向下枚举就行了。后来注意到要求的是最少操作多少次,发现这样不行。因为根据第一行灯的状态只能判断是否可以将其全部变为白色或者黑色。而无法算出最少的操作次数。正确的思路: 因为矩阵规模较小,我们可以暴力。即枚举16种状态,取最小值。即用16位2进制串,0代表不进行操作,1代表进行对应的操作。所有操作执行完以后判断是否全为白色或者全为黑色。如果是则取最小值。
AC代码
#include2. Subsequence
题目链接
题意描述:给定一个长度为N的整数序列,给定一个整数S,求N的最短子序列,子序列的和小于S。
解题思路: 一看就是双指针(尺取法),我们可以发现,当a[i] ~ a[j] 刚好大于S时这是子序列长度为 j - i 此时我们稍加分析可以发现,j指针没有回退的必要。故我们只需要将i指针继续前进然后找到对应的j再于最小值比较即可。
AC代码
#include3.Quasi Binary
题目链接
题意描述:给定一个数n,求他由多少个 01序列组成。01序列:即一个序列中的数只能是 0和1或 1 或 0.输出他需要几个01序列,并输出对应的0 1 序列。要求个数最少。
解题思路: 这道题可能算个思维题??因为每一位只能由0或1组成。。即统计n的每一位1的个数。然后从最高位开始拼凑01串。如果某位个数为0,则01串的该位为0,否则为1.
AC代码
#include4.Protecting the Flowers
题目链接
题意描述:约翰有N头牛在他的花园里。约翰为了防止牛破坏他的花园要将牛牵走,但是牵走每头牛都需要花费对应的时间,每头牛每分钟摧毁花园的面积又不相同。约翰想知道他的花园最少要被摧毁多少面积。
解题思路: 经典贪心,以前一直以为贪心凭直觉,上完课以后才发现贪心是可以推的。。

假设前面已经是最优解,我们现在只需要关心A和B先牵走谁。我们即可写出先牵走A或先牵走B的浪费的面积。则有如下公式。

假设A在B前是最优的,则有a.t/a.d < b.t/b.d。

然后我们就可以发现我们找到了排序的方法。然后排序,模拟就行了。
上诉推导法很重要!
AC代码
#include5.校门外的树
题目链接
题意描述:给定长度为L路,每米有一颗树,然后给出m个区间,将对应区间内的树全部移走。问经过m次后还剩多少棵树。
解题思路: 该题经典差分数组,因为是一个区间减去相同的值,故直接用差分数组即可。
AC代码
#include6.明明的随机数
题目链接
题意描述:输入n个数去重并排序。
解题思路: 由于 n<= 100且元素<=1000故直接桶排。
AC代码
#include7.[HNOI2003]激光炸弹
题目链接
题意描述:一种新型的激光炸弹,可以摧毁一个边长为R的正方形内的所有的目标。
现在地图上有n(N ≤ 10000)个目标,用整数Xi,Yi(其值在[0,5000])表示目标在地图上的位置,每个目标都有一个价值。
激光炸弹的投放是通过卫星定位的,但其有一个缺点,就是其爆破范围,即那个边长为R的正方形的边必须和x,y轴平行。求一颗炸弹能炸掉的最大价值。
解题思路: 二维矩阵前缀和。即求出二维矩阵前缀和以后直接暴力查找维护最大值即可。
求二维矩阵前缀和的方法:
如图求图中橙色区域的前缀和
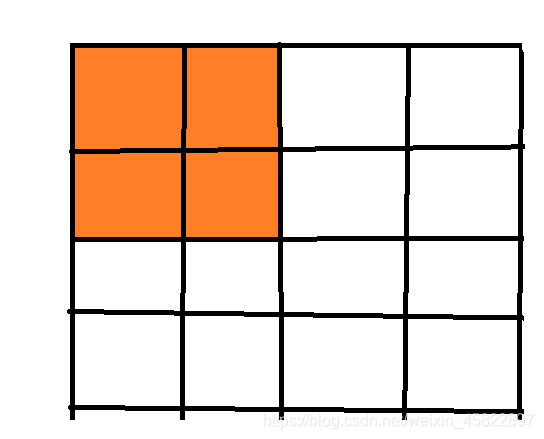
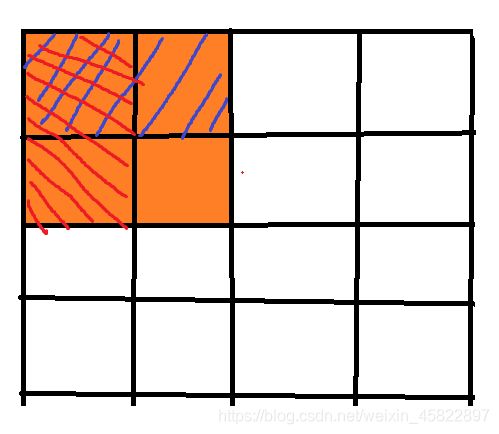
由图可知
求上图中橙色的区域面积 = 蓝色阴影区域面积 + 红色阴影区域 - 红色与蓝色阴影区域交接处的面积 + 当前点的面积。
故可以推出二维矩阵前缀和的通式:
sum[i][j] = sum[i-1][j] + sum[i][j-1] - sum[i-1][j-1] + g[i][j];
同理求对应正方形面积时应让当前节点的前缀和的值-红色阴影区域的面积 - 蓝色阴影区域的面积 + 红色与蓝色阴影区域的面积。
AC代码
#include
using namespace std;
int g[5005][5005];
int sum[5005][5005];
int main(void)
{
int n,r,v,x,y,ans,x0,y0,temp;
scanf("%d %d",&n,&r);
fori(n){
scanf("%d %d %d",&x,&y,&v);
g[x][y] = v;
}
for(int i=0;i<MAX;i++){
//求二维数组的前缀和
for(int j=0;j<MAX;j++){
if(i-1>=0)
sum[i][j] += sum[i-1][j]; //加蓝色阴影区域的面积
if(j-1>=0)
sum[i][j] += sum[i][j-1]; //加红色阴影区域的面积
if( i-1 >= 0 && j-1 >= 0)
sum[i][j] -= sum[i-1][j-1]; //减交集处的面积
sum[i][j] += g[i][j];//加当前值
}
}
ans = INF;
for(int i=0;i<MAX;i++) //求以i,j为右下角顶点的正方形摧毁的总价值
{
for(int j=0;j<MAX;j++)
{
temp = sum[i][j];
x0 = i-r;
y0 = j-r;
if(x0 >= 0)
temp -= sum[x0][j]; //减蓝色阴影区域的面积
if(y0 >= 0)
temp -= sum[i][y0]; //减红色阴影区域的面积
if(x0 >= 0 && y0 >=0)
temp += sum[x0][y0]; //加交集处的阴影面积
if(temp > ans)
ans = temp; //记录摧毁的最大价值。
}
}
printf("%d\n",ans);
return 0;
}
8.铺地毯
题目链接
题意描述:
为了准备一个独特的颁奖典礼,组织者在会场的一片矩形区域(可看做是平面直角坐标系的第一象限)铺上一些矩形地毯。一共有n张地毯,编号从1到n。现在将这些地毯按照编号从小到大的顺序平行于坐标轴先后铺设,后铺的地毯覆盖在前面已经铺好的地毯之上。地毯铺设完成后,组织者想知道覆盖地面某个点的最上面的那张地毯的编号。注意:在矩形地毯边界和四个顶点上的点也算被地毯覆盖。
输出描述:输出共1行,一个整数,表示所求的地毯的编号;若此处没有被地毯覆盖则输出-1。
解题思路: 给顶左下角,和长宽,可以确定所有顶点的位置。不过只需要确定右上角顶点坐标就可以了,就是个模拟。。
AC代码
#include
using namespace std;
struct node{
int x,y;
int lx,ly;
}point[MAX];
int main(void)
{
int n,x,y,ans=-1;
scanf("%d",&n);
fori(n){
scanf("%d %d %d %d",&point[i].x,&point[i].y,&point[i].lx,&point[i].ly);
}
scanf("%d %d",&x,&y);
fori(n){
if( x>=point[i].x && x<= point[i].x + point[i].lx){
if(y >= point[i].y && y <= point[i].y + point[i].ly){
ans=i+1;
}
}
}
printf("%d\n",ans);
return 0;
}
9.纪念品分组
题目链接
题意描述:元旦快到了,校学生会让乐乐负责新年晚会的纪念品发放工作。为使得参加晚会的同学所获得 的纪念品价值相对均衡,他要把购来的纪念品根据价格进行分组,但每组最多只能包括两件纪念品, 并且每组纪念品的价格之和不能超过一个给定的整数。为了保证在尽量短的时间内发完所有纪念品,乐乐希望分组的数目最少。
你的任务是写一个程序,找出所有分组方案中分组数最少的一种,输出最少的分组数目。
解题思路: 贪心加双指针,为了分组数目最少,应该让数值小(指针i)的与数字大(指针j)的结合起来,但它俩的合不应该超过w,如果满足条件 i++,j–。不满足则j–,i不动。
AC代码
#include
using namespace std;
int main(void)
{
int w,n,last,ans = 0;
int p[MAX];
scanf("%d %d",&w,&n);
fori(n){
scanf("%d",&p[i]);
}
sort(p,p+n);
last = n-1;
fori(n){
if(i>last) break;
while( last > i && p[i] + p[last] > w){
last--;
ans++;
}
if(i == last){
//相遇则ans++然后退出
ans++;
break;
}
else{
//没有相遇则last向前移动
ans++;
last--;
}
}
printf("%d\n",ans);
return 0;
}
10.回文日期
题目链接
题目描述: 在日常生活中,通过年、月、日这三个要素可以表示出一个唯一确定的日期。
牛牛习惯用8位数字表示一个日期,其中,前4位代表年份,接下来2位代表月份,最后2位代表日期。显然:一个日期只有一种表示方法,而两个不同的日期的表示方法不会相同。
牛牛认为,一个日期是回文的,当且仅当表示这个日期的8位数字是回文的。现 在,牛牛想知道:在他指定的两个日期之间包含这两个日期本身),有多少个真实存在的日期是回文的。
一个8位数字是回文的,当且仅当对于所有的i ( 1 <=i<= 8 )从左向右数的第i个 数字和第9-i个数字(即从右向左数的第i个数字)是相同的。
解题思路: 模拟,根据年份生成对应的月份和日,然后判断该月改日是否存在即可。
第一次见可以这样读入数据,果然群除我皆佬。
scanf("%4d%2d%2d",&ey,&em,&ed);
还学到了,可以通过比较数值大小来处理起始年和结束年的情况。不用再进行特殊处理。。
AC代码
#include11.拼数
题目链接
题意描述:设有n个正整数(n ≤ 20),将它们联接成一排,组成一个最大的多位整数。
例如:n=3时,3个整数13,312,343联接成的最大整数为:34331213
又如:n=4时,4个整数7,13,4,246联接成的最大整数为:7424613
解题思路: 高位的数越大越好,但不可以直接利用字典序排序,比如 572 57 4 如果按字典序排结果为 572 57 4但正确答案为 57 572 4由于位数不同会导致出现误差,故应该保证排序的字符串位数相同。 即 比较a+b 与 b+a的大小。
AC代码
#include12.毒瘤xor
题目链接
解题思路: 这道题和我原来出的一道题简直一模一样。。区间异或值最大,即使区间中每一位异或值最大。即统计区间中每一位的0或1的个数即可确定x对应位为0或为1。当区间内1的个数多与一半时为x对应位为0,小于一半时为1.同时注意区间查询,应该采用前缀和。
AC代码
#include
#include
#define mem(a,b) memset(a,b,sizeof(a))
using namespace std;
int num[MAX];
int sum[35][MAX]; //sum[i][j] 代表前j个数第i位为1的个数的和。
void solve(int l,int r)
{
int flag = ( (r - l + 1) + 1 ) / 2 ;//半数标志
int temp = 1;
int ac;
int ans = 0;
for(int i=0;i<31;i++)
{
ac = sum[i][r] - sum[i][l-1] //查询区间内第i位有多少个1
if( ac < flag){
ans += temp; //如果小于则说明该位为1需要+对应位的值
}
temp *= 2;
}
printf("%lld\n",ans);
}
int main(void)
{
int n,q,l,r,cnt;
int jz[35]={
0};
scanf("%d",&n);
fori(n){
scanf("%d",&q);
num[i+1] = q;
cnt = 0;
while(q!=0){
//求该数的二进制
if( q % 2 != 0 ) //可以通过 >> & 1 来取二进制
jz[cnt]++;
q /= 2;
cnt++;
}
for(int j=0;j<32;j++)
{
sum[j][i+1] = sum[j][i] + jz[j]; //第i+1位的前缀和 = 前一位的前缀和 + 当前位
jz[j] = 0; //记得清0
}
}
scanf("%d",&q);
fori(q){
scanf("%d %d",&l,&r);
solve(l,r);
}
return 0;
}
13.字符串
题目链接
题意描述:小N现在有一个字符串S。他把这这个字符串的所有子串都挑了出来。一个S的子串T是合法的,当且仅当T中包含了所有的小写字母。小N希望知道所有的合法的S的子串中,长度最短是多少。
解题思路: 经典双指针,用个桶来存各个字母的数量,找到了,记录下长度,然后i指针前移。找不到j指针不断后移。
AC代码
#include
#include
#define forj(n) for(int j=0;j
#define mem(a,b) memset(a,b,sizeof(a))
using namespace std;
int main(void)
{
int vis[30]={
0};
string s;
cin>>s;
int len = s.length();
int ans = INF;
int k = 0;
bool flag;
fori(len){
for(;k<len;k++){
//将指针k移到合适位置,即出现全部小写字母的位置
flag = true;
vis[s[k] - 'a']++;
for(int j = 0 ;j < 26 ; j++){
if(vis[j] == 0){
flag = false;
break;
}
}
if(flag)
{
vis[s[k] - 'a']--; //第二次进入时会重复加,故先减一下。
break;
}
}
if(flag)
{
ans = min(ans,k-i+1);
vis[s[i] -'a']--;//i指针要向前移动,故应该减掉i指针位置的字母
}
else break;//如果不是因为 flag导致的循环退出说明 k走过最后一位了,没有继续搜索的必要了,直接推出循环即可。
}
printf("%d\n",ans);
return 0;
}
14.数学考试
题目链接
题意描述:今天qwb要参加一个数学考试,这套试卷一共有n道题,每道题qwb能获得的分数为ai,qwb并不打算把这些题全做完,
他想选总共2k道题来做,并且期望他能获得的分数尽可能的大,他准备选2个不连续的长度为k的区间,
即[L,L+1,L+2,…,L+k-1],[R,R+1,R+2,…,R+k-1](R >= L+k)。
解题思路: 这道题不会,看了眼题解。大佬写的太强了,不理解可以自己出几组数据细品。因为区间大小是固定为k的,所以显然需要前缀和处理一下
处理之后我们去维护前缀中长度为k的最大值temp,枚举第二个长度为k的起点,那么答案就是max(ma+当前长度为k的序列和)
复杂度为O(n)
极限数据计算 n为2e5,k=1e5 所有ai都是1e5 那么最大值是2e5*1e5>(1<<31)-1 超过了int所能表示的范围 所以需要开long long
AC代码
#include
#include
#define mem(a,b) memset(a,b,sizeof(a))
using namespace std;
ll arr[MAX];
int main(void)
{
int t,n,k;
ll temp;
ll ans;
scanf("%d",&t);
while(t--)
{
ans = -INF;
mem(arr,0);
scanf("%d %d",&n,&k);
for(int i = 1;i<=n;i++)
{
scanf("%lld",&temp);
arr[i] = arr[i-1] + temp;
}
temp = -INF;
for(int i = k; i+k <= n ; i++)
{
temp = max( arr[i] - arr[i-k] , temp );
ans = max(ans,temp + arr[i+k] - arr[i]);
}
printf("%lld\n",ans);
}
return 0;
}
15.「土」秘法地震
题目链接
题意描述:帕秋莉掌握了一种土属性魔法
这种魔法可以在一片k×k大小的一个正方形区域内产生地震
但是如果某片即将产生地震的区域内有建筑物,帕秋莉会停止施法
整个地图大小为n×m,其中一些地方有建筑
请问有多少种可能的情况,使得帕秋莉会停止施法
解题思路: 二维矩阵前缀和,求出前缀和以后遍历,搜索以i,j为右下顶点的正方形的和是否>=1 如果>=1 ans++。
AC代码
#include
#include
#define mem(a,b) memset(a,b,sizeof(a))
using namespace std;
int sum[1005][1005];
char g[1005][1005];
int main(void)
{
int n,m,k,ans = 0,temp;
scanf("%d %d %d",&n,&m,&k);
for(int i = 0 ; i < n ; i++){
//求二维矩阵前缀和
getchar();
for(int j=0;j<m;j++){
scanf("%c",&g[i][j]);
sum[i][j] = g[i][j]-'0';
if( i-1 >= 0 ) sum[i][j] += sum[i-1][j];
if( j-1 >= 0) sum[i][j] += sum[i][j-1];
if( i-1 >= 0 && j-1 >= 0) sum[i][j] -= sum[i-1][j-1];
}
}
for(int i=k-1;i<n;i++){
//因为为长度为k的正方形,故直接从k行k列开始
for(int j=k-1;j<m;j++){
temp = sum[i][j];
if( i-k >= 0) temp -= sum[i-k][j];
if( j-k >= 0) temp -= sum[i][j-k];
if( i-k >= 0 && j-k >= 0 ) temp += sum[i-k][j-k];
if(temp > 0) ans++;
}
}
printf("%d\n",ans);
return 0;
}
16.丢手绢
题目链接
题意描述:牛客幼儿园的小朋友们围成了一个圆圈准备玩丢手绢的游戏,但是小朋友们太小了,不能围成一个均匀的圆圈,即每个小朋友的间隔可能会不一致。为了大家能够愉快的玩耍,我们需要知道离得最远的两个小朋友离得有多远。因为是玩丢手绢,所以小朋友只能沿着圆圈外围跑,所以我们定义两个小朋友的距离为沿着圆圈顺时针走或者逆时针走的最近距离。
解题思路: 双指针,求最远距离,即求出距离每一位小朋友最远的小朋友的距离,取最大值。,每一位 小朋友距离的最大值,可以比较容易的发现,当顺时针的距离总距离的一半时,指针r++,直到不满足,说明这个小朋友的位置或者前一位的小朋友到i指针指向的小朋友距离比其他的都远。

即 6 或 5 小朋友离1小朋友距离最远。然后计算小朋友2的最远的小朋友,可以知道,指针r不需要回退,继续往前走。直到不满足顺时针的距离小于总距离的一半时。即可找到。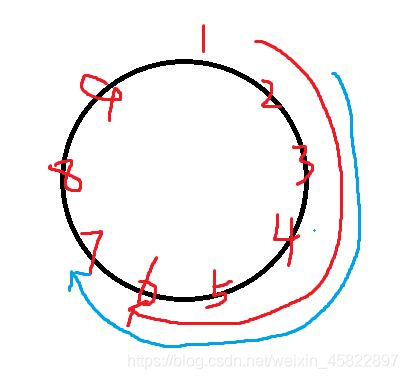
AC代码
#include
#include
#define mem(a,b) memset(a,b,sizeof(a))
using namespace std;
int dis[MAX];
int main(void)
{
int n,r=0,rlen,ans = -2147483647,sum = 0,temp;
scanf("%d",&n);
fori(n){
scanf("%d",&dis[i]);
sum += dis[i];
}
rlen = dis[0];
for(int i=0;i<n;i++)
{
while( rlen <= sum/2 ){
//找到对应位置
r++;
rlen += dis[r%n];
}
temp = sum - rlen; //记录这一位的最短距离
rlen -= dis[r%n]; //前一位的最短距离
r--;
ans = max(ans,max(rlen,temp)); //取最大值
rlen -= dis[i]; //i指针前移。
}
printf("%d\n",ans);
return 0;
}
