北京化工大学2021年ACM寒假专题训练（一）（Python版）
北京化工大学2021年ACM寒假专题训练（一）
-
问题 A: a^b
Python的pow()
pow(a,b)返回
的值，pow(a,b,p)则返回
的值,所以直接print(pow(a,b,p))就可以了
分析
作为一个算法竞赛萌新，，我首先想到的是直接计算么，先算s=a^b,再算s%p,不就OK了，直接print(a**b%p)不就可以，但是当ａ，ｂ，ｐ很大时，运算超时了，这种方法是不可取的，这里需要快速幂取模。
快速幂
首先我们先看一个简单的问题，
怎么算，很简单，
，２连续乘几下２就出结果了，那
呢？那直接再连续乘多个２，就可以了，但是有没有可能减少运算次数呢？
可以想到 
，
可以经过一次计算得到，所以
所以前者需计算15次（
），后者计算4次（
一次，
两次，
三次，
四次），减少了运算次数
一个数可表示成二进制，比如 b 可以为
，
那么可得到
乘法取模公式 ![(A\times{B})modc = [ (AmodC)\times{(BmodC)} ] modC](http://img.e-com-net.com/image/info8/916e432275934dfeab19e4512352785e.gif)
Python代码实现
- 所以根据以上两个公式得到代码
a,b,p=map(int,input().split())
ans=1
while b>0:
if b&1==1:
ans*=a%p
a=a*a%p
b>>=1
print(ans%p)
到OJ上测试正确了
- 还有print(pow(a,b,p))
a,b,p=map(int,input().split())
print(pow(a,b,p))
正确没有超时，可以和前者比较，发现内存相同，运行时间288MS>138MS,但是代码很简洁，也是个不错的选择，python好强大啊。
- 那么直接print(a**b%p)呢？
a,b,p=map(int,input().split())
print(a**b%p)#注：**表示平方，%表示mod（取模）测试一下，果然超时了
以上就是我做A题的过程与一些思考。
-
问题 B: 64位整数乘法
分析
a与b都为long long型整数，Python完全支持大整数，所以直接print(a*b%p)就可以
Python代码实现
注意题目要求三行输入，可得代码
a=int(input())
b=int(input())
p=int(input())
print(a*b%p)放入OJ中测试，显示正确
-
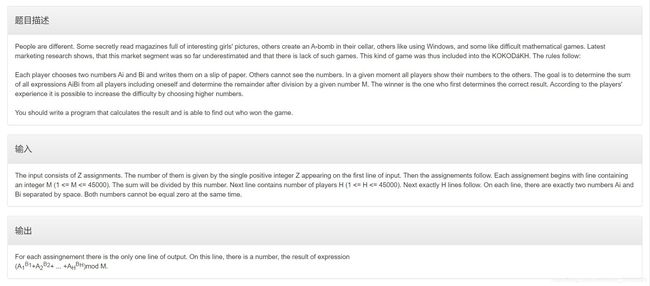
问题 C: Raising Modulo Numbers
分析
看到这么长的英文，首先我觉得很难，但看懂题后，其实就是A题的升级版，就是求每个测试样例
的值，基于A题的快速幂取模，对于，可以运用递归来求值，用到公式
,比如计算
时，可以先将
当作一个整体，求得值，而
，从而实现求值，类似地，同样适用于很多个加数。
Python代码实现
Python3已经支持中文命名，所以我尝试运用了中文名称命名，定义快速幂取模、递归取模两个函数，对于每个测试样例，将答案添加进ans列表中即可
z=int(input())#测试样例数
ans=[]
def 快速幂取模(a, b, p):
ans = 1
while b > 0:
if b & 1 == 1:
ans *= a % p
a = a * a % p
b >>= 1
return ans % p
def 递归取模(nums,x):
if len(nums)==1:
return 快速幂取模(nums[0][0],nums[0][1],x)
else:
First=快速幂取模(nums[0][0],nums[0][1],x)
return (First+递归取模(nums[1:],x)%x)%x
for i in range(z):
M=int(input())
H=int(input())
ABlist=[]
for j in range(H):
ABlist.append([int(k) for k in input().split()])
ans.append(递归取模(ABlist,M))
for 答案 in ans:
print(答案)
放在OJ中测试，AC(Accepted)了，还说明Python支持的中文名称很好用哈，Py友们可以尝试命名中文名称，还不错哦。
