灰色关联度分析excel步骤_基于灰色理论的旅游需求预测算法分析

 灰色理论 

灰色理论是以“部分信息已知,部分信息未知的小样本、贫信 息”不确定性系统为研究对象的一门系统科学。今天我们利用灰色预测模型对旅游需求作中短期预测预报。

旅游市场就是一个复杂的、不确定性的巨大灰色系统,影响其发展的因素对旅游市场的发展表现出明显的灰色性。因此,可以将旅游市场作为一个灰色系统来研究,引入灰色预测模型GM(1,1)和GM(1,N)来进行研究。

灰色系统理论的旅游需求预测模型 

 建立 GM(1,1)模型作初步预测

设

为各年的旅游人数。

为 x₀ 的一次累加序列;

其中

则可建立灰色预测GM(1,1)模型:

其中, d (k) 为的灰导数;

z⁰₍₁₎   为 x⁰₍₁₎ 的均值数列 ,

将 x₀⁽⁰⁾(2) ,…,  x₀⁽⁰⁾ (n) 带入方程得到:

利用最小二乘法求解:

其中: u = ( a，b)^T ,

根据以上方程即可得 a 和 b 的值,反演回方程(1)即可得到旅游 人数的预测结果。 

由GM(1,1)灰微分方程(1)所对应的白化微分方程。

即可得到旅游人数的预测结果。 

GM(1,N)模型建立 

由于旅游需求受多方面因素的影响,简单的GM(1,1)模型并不 能反映各个因素的作用,模型需要进行优化,为了使预测更加精确,需要把旅游资源、环境、交通、费用、服务质量、客源地人口等因素考虑在模型里考虑在内,建立GM(1,N)模型。

求解此模型的方法与GM(1,1)相似,求得参数 a 和 b_i 的值,进 而求得GM(1,N)模型的解可表示为:

从以上分析得到,只需要确定参数和的值,就可以求得每年相 应的游客人数,即旅游需求数。而多元灰色模型中影响旅游的因素 x_i 需要进行无量纲化处理,所以首先要对各影响因素进行无量纲归一化处理。然后再进行灰色关联分析,得到各因素 x_i 与因子 x₁ 的关联度,才能顺利的进行 GM(1,N)模型求解。

对北京地区旅游需求的预测 

首先确定影响旅游需求的因素,列出多种可以用来表示该因子的数据类型,进而展开数据的采集工作。经调查得到，影响北京市旅游需求的因素主要包括:旅游资源、环境、交通、费用、服务质量、客源地人口等。对这些因素进行无量纲归一化数据处理,得 到的调查结果如表1。

以上7个因子对旅游需求即游客数的影响建立GM(1,N)模型 (5),并利用GM(1,1)模型相似的方法进行求解。令:

代入模型(5),根据最小二乘法进行计算得到参数 a 和 b_i 的值如下：

(a,b2 ,... ,b7)=(0.0002-0.0108-0.1237-0.1617-0.0024 - 0.0138 - 0.0103)

将所得的参数代入模型(6)可以得到灰色预测模型的游客数量推测值如表2。 

绘制推测值与实际值的对比如图1。 

从图中可以看出推测曲线与实际曲线吻合度很好,最大相对 误差约为%1,得到的预测精度很高。下面对以上模型进行检验：

均相对误差为:

精度等级为一级。

计算原始序列x₀⁽⁰⁾ 的均方差为:

求残差 δ 的均方差为:

计算方差比

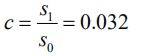
根据模型预测等级划分,该模型的预测等级为“好”,因此该模型是十分合理的。

从以上分析可以看出,基于灰色系统理论的旅游需求预测模 型的预测效果显著,和北京当地旅游的实际情况基本相符,具有很好的预测精度和很高的应用价值。且由于灰色系统理论的“黑箱” 效果,该模型可以进行广泛推广,随着旅游业的发展,将会应用到 更多的旅游市场分析领域。

•  END  •

模友们可能已经发现：现在公众号推送文章的顺序，已经不会按时间排列了。这种变化，可能会让各位模友错过我们每天的推送。

所以，如果你还想像往常一样，聚焦数模乐园，就需要将“数模乐园”标为星标公众号，同时在阅读完文章后，别忘了给一个“在看”哦。

星标步骤

(1)点击页面最上方“数模乐园”，进入公众号主页

(2)点击右上角的小点点，在弹出页面点击“设为星标”，就可以啦。

扫码关注我们

2020国际赛QQ参赛群

球分享

球点赞

球在看