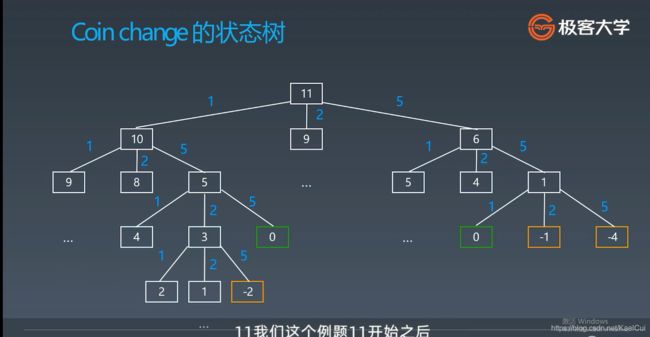
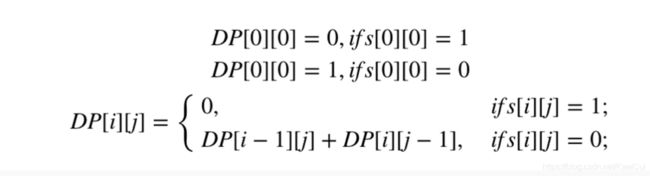【leetcode】动态规划62、1143、70、120、53、152、322、279、72、55、45、62、63、980

62. 不同路径

class Solution:
    def uniquePaths(self, m: int, n: int) -> int:
        aux = [[1 for x in range(n)] for x in range(m)]  # 他这里是将所有的元素都初始话为1的
        
        for i in range(1, m):
            for j in range(1, n):
                aux[i][j] = aux[i-1][j] + aux[i][j-1]  # 这里的配置是存储所有的数据，但是实际上可以类似于斐波那契数列那样只存一维的值，这样时间复杂度没有变化，但是空间复杂度提高了
        return aux[-1][-1]  

class Solution:
    def uniquePaths(self, m: int, n: int) -> int:
        aux = [[1] * n for x in range(m)]
        # aux = [[1 for x in range(n) for x in range(m)]]  这行代码等价于上一个，只是这样写的话更加有普遍意义
        for i in range(1, m):
            for j in range(1, n):
                aux[i][j] = aux[i-1][j] + aux[i][j-1]
        return aux[-1][-1]  

1143. 最长公共子序列

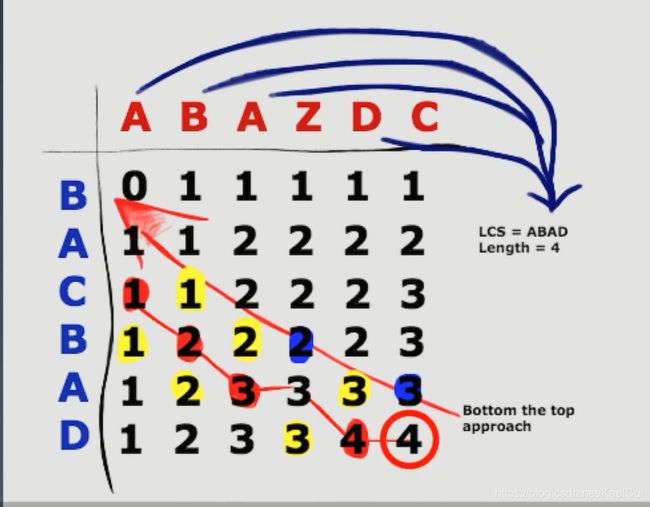
这里将俩个需要对比的子串分为俩个维度上面，值的大小就是当前位置的最长公共子序列



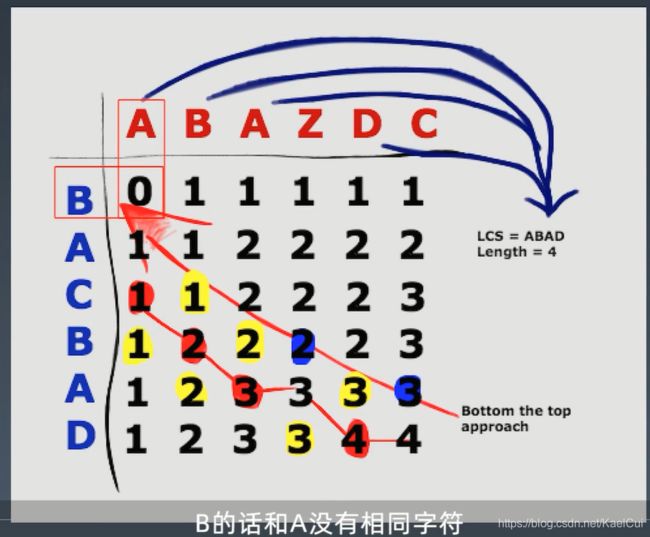
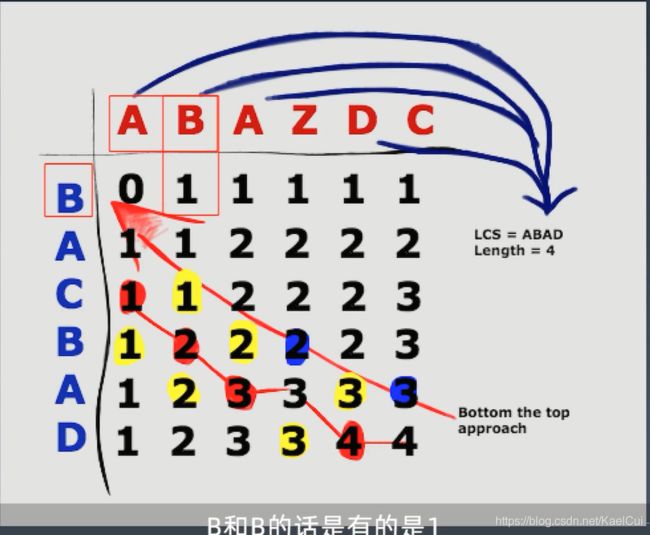
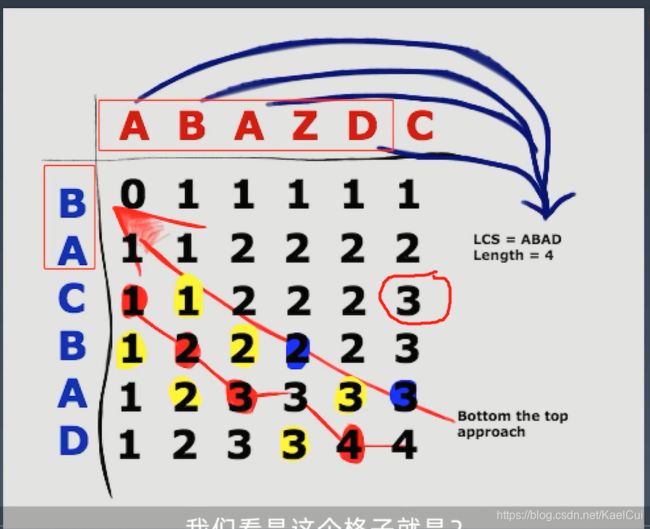
转化问题的思路

对于第二种情况来说其实就是，去掉公共部分再求最长公共子序列，因为已经知道有一个子序列，所有在结果上面加1

class Solution:
    def longestCommonSubsequence(self, text1: str, text2: str) -> int:
        if not text1 or not text2:
            return 0 
        m, n = map(len,(text1, text2)) 
        dp = [[0] * (n+1) for _ in range(m + 1)]
        for i in range(1, m + 1):
            for j in range(1, n + 1):  
                if text1[i-1]  == text2[j-1]:  
                    dp[i][j] = 1 + dp[i-1][j-1]   
                else:  
                    dp[i][j] = max(dp[i-1][j], dp[i][j-1])  
        return dp[m][n] 

简化的代码结构

class Solution:
    def longestCommonSubsequence(self, text1: str, text2: str) -> int:
        dp = [[0] * (len(text2) + 1) for _ in range(len(text1) + 1)]
        for i, c in enumerate(text1):
            for j, d in enumerate(text2):
                dp[i + 1][j + 1] = 1 + dp[i][j] if c == d else max(dp[i][j + 1], dp[i + 1][j])
        return dp[-1][-1]

70. 爬楼梯

class Solution:
    def climbStairs(self, n: int) -> int:
        a, b = 0, 1
        for _ in range(n):
            a, b = b, a + b 
        return b

120. 三角形最小路径和

53. 最大子序和

class Solution:
    def maxSubArray(self, nums: List[int]) -> int:
        '''
        DP:
        dp[i] = max(nums[i], nums[i] + nums[i-1] )
        最大子序和 = 当前元素自身最大（这里的意思是之前的是负值已经舍弃掉了，或者包含之前 后最大
        '''
        dp = [nums[0]] * len(nums)  # 这里是用nums里面的第一个值进行初始话dp这个数组
        for i in range(1, len(nums)):
            # dp[i] = max(nums[i], nums[i] + dp[i-1])  # 这里仍然是用nums是为了复用 nums这块空间
            dp[i] = nums[i] + max(0, dp[i-1])  # 利用max求和函数的性质，把求最大的公共部分的值提取出来，进行代码结构的调整
        return max(dp)     

152. 乘积最大子数组

class Solution:
    def maxProduct(self, nums: List[int]) -> int:
        min_prod = max_prod = res  = nums[0]
        for i in range(1, len(nums)):
            if nums[i] < 0:
                min_prod, max_prod = max_prod, min_prod  # 要考虑负负得正的情形
            max_prod = max(max_prod * nums[i], nums[i])
            min_prod = min(min_prod * nums[i], nums[i])
            res = max(res,  max_prod)
        return res  

322. 零钱兑换

此题目的三种解法：

• 1. 傻递归：复杂度是指数级别的
• 2. BFS： 写出来递归状态树，然后广度优先，找到每一层里面最早出现0的这个就是我们要的层数
• 3. DP: 就是类似于” 爬楼梯”问题，就是将问题拆分为减去每阶的台阶数， 然后 再加上 第k台阶数这个需要的1次
• 

class Solution:
    def coinChange(self, coins: List[int], amount: int) -> int: 
        dp = [0] + [float('inf')] * amount
        for i in range(1, amount + 1):
            for k in coins:
                if i - k >= 0:  # 这里是找到所有在 coins里面可以拆分的子问题
                    dp[i] = min(dp[i], dp[i-k] + 1)
        return [dp[amount], -1][dp[amount] == float('inf')]

279. 完全平方数

class Solution:
    def numSquares(self, n: int) -> int:
        dp = [0] +[float('inf')] * n 
        for i in range(1, n + 1):
            dp[i] = min(dp[i - j * j] for j in range(1, int(i ** 0.5) + 1)) + 1
        return dp[n]  

72. 编辑距离

class Solution:
    def minDistance(self, word1: str, word2: str) -> int:
        m, n = map(len,(word1, word2))
        # 有一个字符串为空串
        if n * m == 0:
            return n + m
        table = [[0] * (n + 1) for _ in range(m + 1)]  # dp数组初始化
        
        # 边界状态初始化
        for i in range(m + 1):
            table[i][0] = i
        for j in range(n + 1):
            table[0][j] = j

        for i in range(1, m + 1):
            for j in range(1, n + 1):
                if word1[i - 1] == word2[j - 1]:
                    table[i][j] = table[i - 1][j - 1]
                else:
                    table[i][j] = 1 + min(table[i - 1][j], table[i][j - 1], table[i - 1][j - 1])
        return table[-1][-1]

参考动画

55. 跳跃游戏
DP definition: The farthest index we can reach given allowed steps from 0 to i
DP decision & relationship: It’s either the dp[i - 1] or i + nums[i] whichever one is larger
DP condition:
If at any moment, dp[i] = 0, that means there is no way it can reach any further, return False immediately.
If at any moment, dp[i] >= last index, that means it can already reach the end of the array given the steps allowed from 0 to i, return True immediately.
参考链接

class Solution(object):
    def canJump(self, nums):
        length = len(nums)
        dp = [0] * length
        dp[0] = nums[0]
        
        for i in range(1, length - 1):
            if dp[i - 1] < i:  # 就是假如在第i-1个位置到不了第i个位置，那么直接判断为 False
                return False
            
            dp[i] = max(i + nums[i], dp[i - 1])
            if dp[i] >= length - 1:
                return True
        
        return dp[length - 2] >= length - 1  # 意思是可不可以取到最后一位的位置

45. 跳跃游戏 II

class Solution:
    def jump(self, nums: List[int]) -> int:
        dp = []    
        curr = 0 
        prev = -1 
        while curr < len(nums) - 1: 
            max_reach = self.get_max_reach(nums[prev+1:curr+1]) 
            dp.append(max_reach) 
            prev = curr 
            curr += dp[-1] 
            if curr == prev: return 0 
        return len(dp)
    
    def get_max_reach(self, arr):
        out = 0
        for i,v in enumerate(arr):
            out = max(out, (i+1+v) - len(arr))
        return out

62. 不同路径

class Solution:
    def uniquePaths(self, m: int, n: int) -> int:
        aux = [[1] * n for x in range(m)]
        # aux = [[1 for x in range(n) for x in range(m)]]  这行代码等价于上一个，只是这样写的话更加有普遍意义
        for i in range(1, m):
            for j in range(1, n):
                aux[i][j] = aux[i-1][j] + aux[i][j-1]
        return aux[-1][-1]

63. 不同路径 II

class Solution:
    def uniquePathsWithObstacles(self, obstacleGrid: List[List[int]]) -> int:
        m, n = map(len, (obstacleGrid,obstacleGrid[0]))
        dp = [[0]*n for _ in range(m)]
        dp[0][0] = 1 if obstacleGrid[0][0] == 0 else 0  # 这里是看下dp[0][0]是不是障碍物，要是障碍物，则设置为0，不是障碍物则设置为1

        for i in range(m):
            for j in range(n):
                if obstacleGrid[i][j] == 1:
                    dp[i][j] = 0
                else:
                    if i-1>=0:
                        dp[i][j] += dp[i-1][j]
                    if j-1>=0:
                         dp[i][j] += dp[i][j-1]
        return dp[-1][-1]

980. 不同路径 III

class Solution:
    def uniquePathsIII(self, grid: List[List[int]]) -> int:
        def dfs(i, j, walks):
            if i<0 or j<0 or i>m-1 or j>n-1 or grid[i][j]==-1:
                return 0
            if grid[i][j] == 2:
                return 1 if walks == 0 else 0
            if walks == 0:
                return 0
            res = 0
            grid[i][j] = -1
            for dir_ in ((1, 0), (-1, 0), (0, 1), (0, -1)):
                new_i, new_j = i + dir_[0], j + dir_[1]
                res += dfs(new_i, new_j, walks-1)
            grid[i][j] = 0
            return res

        walks = 0
        m, n = map(len, (grid, grid[0]))
        if m == 0:
            return 0

        for i in range(m):
            for j in range(n):  
                if grid[i][j] == 1:  # 这里表示是起始方格
                    start = (i, j)
                elif grid[i][j] == 0: # 这里表示是走过的方格
                    walks += 1
        res = dfs(start[0], start[1], walks+1)
        return res

518. 零钱兑换 II

class Solution:
    def change(self, amount: int, coins: List[int]) -> int:
        dp = [1] + [0] * amount        
        for i in coins:
            for j in range(i, amount + 1):                
                dp[j] += dp[j - i]                   
        return dp[amount]