蓝桥杯模拟赛2（大学生组&青少年组）赛后试题解析（C实现）

1.试题A：完美车牌 5’
描述
有一些数字可以颠倒过来看，例如0、1、80、1、8颠倒过来还是本身，66颠倒过来是99，99颠倒过来看还是66，其他数字颠倒过来不构成数字。

类似的，一些多位数也可以颠倒过来看，比如106106颠倒过来是901901.

假设某个城市的车牌只由66位数字组成,每一位都可以取00到99。请问这个城市最多有多少个车牌180°180°倒过来恰好还是原来的车牌?

例如：车牌号：886988886988,倒过来还是886988886988

【答案提交】

这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一个整数，在提交答案时只填写这个数字，填写多余的内容将无法得分。

Python语言选手
print(“你的答案”)

C/C++语言选手
#include

int main()

{

printf("你的答案");

return 0;

}

Java语言选手
public class Main{
public static void main(String[] args){
System.out.println(“你的答案”);
}
}

一共有6个空。
我们先看最外层的1， 6层怎么填。
因为要满足反转，所以我们要考虑反转后一定要对称。
那么我们可以选择 （0，0）（1， 1）（8， 8）（6， 9）（9， 6）
再考虑2， 5层 同样有 这五种情况。
3，4层 同样。
具有对称性
那么根据排列组合。一共有5 * 5 * 5 = 125种情况。
————————————————
版权声明：本文为CSDN博主「是水还是流年」的原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/weixin_43960370/article/details/104447932
代码（C实现）

#include
int main()
{
     
    int  a[10];
   a[0] = 1;
   a[1] = 1;
   a[2] = 0;
   a[3] = 0;
   a[4] = 0;
   a[5] = 0;
   a[6] = 1;
   a[7] = 0;
   a[8] = 1;
   a[9] = 1;
    int count = 0;
    for(int i = 0; i < 10; i++)
    {
     
        
        for(int j = 0; j < 10; j++)
        {
     
           

            for(int k = 0; k < 10; k++)
            {
     
                if(a[i] == 1 &&a[j] == 1 && a[k] == 1)count ++;

            }
        }
    }
    printf("%d",count);
    return 0;
}

2. 试题B：完美日期 5’
   描述
   【问题描述】

   不知天上宫阙，今夕是何年。

   对于完美日期yyyy/mm/dd，wlxsq的定义是:

年月日中均没有出现数字4，
年月日的数位之和是8的倍数
例如：2020/02/02 就是一个完美日期，没有出现数字4，且数位之和是8的倍数。

wlxsq想知道从2020/02/22开始，第88个完美日期是哪个？

【答案提交】

   这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一个格式yyyy/yy/dd，在提交答案时直接填写这个日期，注意需要如果答案有前导零则不能忽略，填写多余的内容将无法得分。

模拟即可。
到每一月的月末，就变到新的一月。
到每一年的年末，就变到新的一年。
注意判断一下闰年的
22
2月份是
2929
29天即可。
答案：
2022/03/072022/03/07
2022/03/07
代码：

#include
int dx[]={
     0,31,29,31,30,31,30,31,31,30,31,30,31};
bool check(int x){
     
	if( x % 400 == 0) 
	    return true;
	else if( x % 4 ==0 && x % 100 != 0)
	    return true;
	else 
	    return false;
}

int p(int x,int y,int z){
     
	int res = 0;
	int flag = 1;
	while( x > 0){
     
		res += x % 10;
		if( x % 10 == 4) flag = 0;
		x /= 10;
	}
	while( y > 0){
     
		res += y % 10;
		if( y % 10 == 4) flag = 0;
		y /= 10;
	}
	while( z > 0){
     
		res += z % 10;
		if( z % 10 == 4) flag =0;
		z /= 10;
	}
	if( flag && res % 8 == 0)  return 1;
	else 
	   return 0;
}

int main(){
     
	int x,y,z;
	int ans = 0;
	x = 2020; y = 2 ; z = 22;
	while(ans < 88){
     
		z++;
		if(check(x) && y==2){
     
			if( z > 28){
     
				z = 1;
				y++;
			}
		}
		else if( z > dx[y]){
     
			z = 1;
			y++;
		}
		if( y > 12){
     
			x++;
			y = 1;
		}
		if(p(x,y,z)){
     
			ans++;
			printf("%d %d %d\t%d\n",x,y,z,ans);
		}
	}
return 0;
}

3.C. 试题C：天机锁10’
描述
【问题描述】
天机锁，锁天机~
wlxsq在机缘巧合的情况下就获得一把天机锁。wlxsq迫不及待的想打开这把锁。该锁的密码是由八个数字构成的,每个数字都是[0,9]中的一个~
锁上面写道：
水(数字9)火(数字4)相生相克,同现同隐(要么都出现，要么都不出现),数量一致(且出现则数量得一样多)。
土(数字2)乃大地，为伊始(数字2一定出现)。
世间万物，不过五二(八个数字之和不超过52)。
此乃天机，一日一次之~
由于天机锁一天只能试一次，wlxsq想知道，总共有多少种方案~

【答案提交】
这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一个数字，在提交答案时直接填写这个数字，填写多余的内容将无法得分。
方法一：
8个
for循环，枚举所有的情况，逐一判断即可~
方法二：
8个坑，
dfs一遍，对于每一种情况逐一判断即可。
答案：
19811435

代码（C实现）：

#include
int a[10];
typedef long long ll;
const int M = 0x7fffffff;
ll ans = 0;

void print(){
     
	for(int i = 1; i <= 8; i++)
	   printf("%d ",a[i]);
	printf("\n");
}

bool check(){
     
	int flag = 0;
	int x = 0, y = 0;
	int sum = 0;
	for(int i = 1; i <= 8; i++){
     
		sum += a[i];
		if(a[i] == 2)
		    flag = 1;
		else if( a[i] == 9)
		    x++;
		else if( a[i] == 4)
		    y++;
	}
	if( flag && x==y && sum<=52)
	    return true;
	else
	    return false;
}

void dfs(int i){
     
	if( i > 8){
     
		if(check()){
     
			ans++;
			if( ans > 100 && ans < 120)
			    print();
		}
		return;
	}
	for(int j = 0; j < 10; j++){
     
		a[i] = j;
		dfs(i + 1);
		
	}
}

int main()
	{
     
	dfs(1);
    printf("%d",ans);
	return 0;
}

4.完美运算 10‘
描述
定义a1:表示数字A对应的三进制数位中1的个数
定义a2:表示数字A对应的三进制数位中2的个数
定义完美运算A○B，如果∣a1−a2∣=∣b1−b2∣,A○B的值为1，否则为0.请问，在[1,2020] 区间，有多少对
(A,B)的结果为
1
例如：A=2,B=3则
a1=0,a2=1,b1=1,b2=0，满足
∣a1−a2∣=∣b1−b2∣所以
A○B的结果为1。
注意，
A=2,B=3构成的数对(2,3)与
A=3,B=2构成的数对(3,2)算同一对。
更新：(2,2)也算一对哦~
【答案提交】
这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。
枚举所有的数字A和所有的数字B。
然后将这两个数转成三进制，计算出a1和a2的值。
答案：
472701
代码（C实现）：

#include
#include
typedef long long ll;
ll a[2050],b[2050];
void p(){
     
	for(int i = 1; i <= 2020; i++){
     
		int m = i;
		while( m > 0){
     
			if( m % 3 == 1) 
			    a[i]++;
			else if( m % 3 == 2)
			    b[i]++;
			m /= 3;
		}
	}
}

int main(){
     
	p();
	ll ans = 0;
	for(int i = 1; i <= 2020; i++){
     
		for(int j = i; j <= 2020; j++){
     
			if( abs(a[i]-b[i]) == abs(a[j]-b[j])){
     
			    ans++;
				if( ans < 10) 
				    printf("%d",i+" ""%d",j );
			}
		}
	}
printf("%d",ans);

	return 0;
}

5.试题E：三叉神树 15’

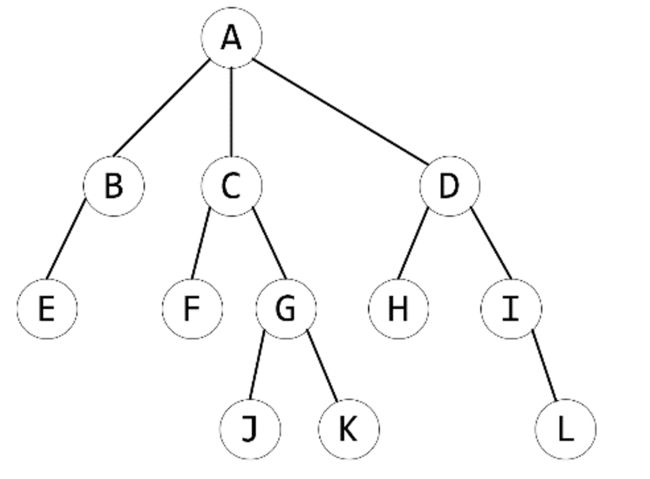
图1
给定如图1所示三叉树，节点A为根节点，E，F，J，K，H，L为叶子节点。已知这12个节点的权值对应着数字[1,12],使得所有以非叶子节点为根的子树权值之和为偶数。

如下图2所示，为其中一种满足要求的方案。

图2样例解释：

对于非叶子节点B：3 + 1 = 4
对于非叶子节点C：5 + 11 + 9 + 7 + 2 = 34
对于非叶子节点G：9 + 7 + 2 = 18
对于非叶子节点D：10 + 8 + 6 + 4 = 28
对于非叶子节点I：6 + 4 = 10

请求出所有满足条件的方案数！！
叶子节点：一棵树当中没有子结点（即度为0）的结点称为叶子结点
【答案提交】

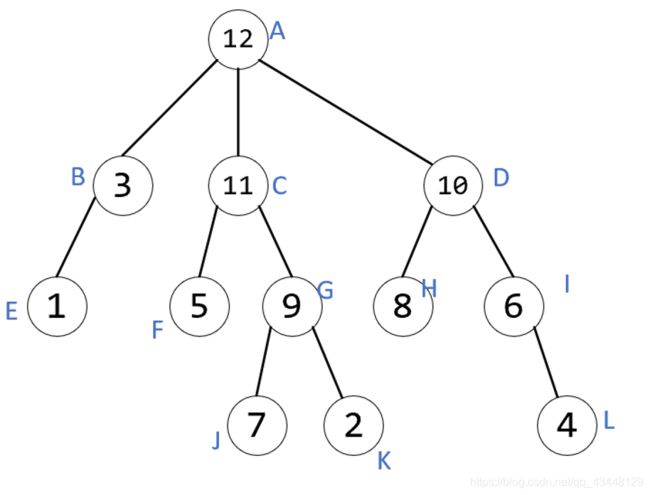
图2
这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

#include
typedef long long ll;
int a[15];
int vis[15];
ll ans = 0;

void print(){
     
	for(int i = 1; i <= 12; i++)
	    printf("%d ",a[i]);
	printf("\n");
}

bool check(){
     
	int x = a[2] + a[5];
	if( x % 2 == 1)
	    return false;
	x = a[7] + a[8] + a[9];
	if( x % 2 == 1)
	    return false;
	x += a[6] + a[3];
	if( x % 2 == 1)
	    return false;
	x = a[11] + a[12];
	if( x % 2 == 1)
	    return false;
	x += a[4] + a[10];
	if( x % 2 == 1)
	    return false;
	return true;
}

void dfs(int i){
     
	if( i > 12){
     
		if(check()){
     
			ans++;
			if(a[1] == 12 && a[2] == 3 && a[5] == 1)
			   print();
		}
		return ;
	}
	for(int j = 1; j <= 12; j++){
     
		if(!vis[j]){
     
			a[i] = j;
			vis[j] = 1;
			dfs(i + 1);
			vis[j] = 0;
		}
	}
}

int main(){
     
	dfs(1);
	printf("%d",ans);

	return 0;
}

6.试题F：JM斗牛 17’
描述
JM打完麻将，觉得太简单了，所以决定去斗牛，挑战一下高难度。
一副牌共54张牌，即采用牌大王(1张),小王(1张),K，Q，J，10，9，8，7，6，5，4，3，2，A。除了大小王，其余牌型均为4张。故4*13+2=54张
斗牛则是每人5张牌，计算5张牌的构成的点数，然后比较点数大小。
关于点数计算：
大王(S)，小王(S)，K，Q，J都当成是10点，A当成是1点，其余牌都当其本身的点数。 大王，小王均用大写字母S表示
每位玩家5张牌，玩家用手上任意的3张牌组合（且只能用3张牌组成10的倍数），使其点数之和为10的倍数，这样就称之为“牛”。
然后将剩余的2张牌点数之和取个位数，如这2张牌之和也为10的倍数，则组成“牛牛”牌型。如这2张牌之和不为10的整数倍，则去掉十位数之后个位数为几，则成为“牛几”牌型。
如任意三张牌组合的点数之和都不能成为10的倍数，则称之为“无牛”牌型。
例如：
牛牛牌型:选取的3张牌之和为10的整数倍,余下2张牌之和也为10的整数倍。例：A,9,10,J,Q.选取(A,9,J)和为10的整数倍,(10,Q构成)牛牛
牛九牌型:选取的3张牌之和为10的整数倍,余下2张牌之和的个位数为9。例：A,9,10,J,9。   
牛八牌型:选取的3张牌之和为10的整数倍,余下2张牌之和的个位数为8。例：A,9,10,J,8。
牛七牌型:选取的3张牌之和为10的整数倍,余下2张牌之和的个位数为7。例:A,9,10,J,7。选取(A,9,J)和为10的整数倍，(10,7构成)牛七
无牛牌型: 任意选取的3张牌之和均不可能为10的整数倍例:A,9,8,9,7。
JM会打麻将，但是不怎么会斗牛，想请你帮忙编写程序帮忙计算一下，JM 拿到的牌是什么牌型。
输入
输入一行包含5个字符，表示5张牌。
输出
输出一行表示牌型。数字1~9表示牛一至牛九，如果是牛牛牌型，则输出“so cool!”,如果是无牛排序，则输出“so sad!”
样例
输入
复制
A 2 3 5 S
输出
复制
1
输入
复制
S S A 8 8
输出
复制
so sad!
输入
复制
S S J Q K
输出
复制
so cool!

答案：首先，我们证明答案是唯一的：
对于
J,Q,K,S都转换称数字
10,记这5张牌的点数分别为
a1,a2…a5
，记录
sum=∑i=15ai
记录答案为牛x牌型。牛牛牌型其实就是牛0牌型。
如果存在i,j,k，使得ai+aj+ak为10的倍数，那么
x=(sum−ai−aj−ak)%10，所以x其实就是x%10
所以答案唯一。
其次，我们可以枚举所有可能的三元组(i,j,k)，判断这三张牌点数之和是否为10的倍数即可。
5个数全排列一下就可以了~
代码（C实现）：

#include
#include
#define N 100
int bag[N]={
     0};
int book[N]={
     0};
int n=5;
int flag=0;
int max0=0;
void dfs(int num,int sum ){
     
	if( num==4 ){
     
		if( sum%10==0 ){
     
			flag=1;
			int k,ss=0;
			for( k=1;k<=n;k++ ){
     
				if( book[k]==0)
						ss+=bag[k];
			}
			
			if( ss%10==0 )
			  max0=100;
			
			if( ss%10>max0 )
			max0=ss%10;
		}
		
		return ;
	}
	
	int i;
	for( i=1;i<=n;i++  ){
     
		
		if( book[i]==1 )
		continue;
		
		book[i]=1;
		
		dfs( num+1,sum+bag[i]);
		
		book[i]=0;
		
	}
	return ;
}
int main(){
     

    int i,j,k;
	char s[N];
	gets( s );
	int cnt=1;
	for(i=0;i<strlen(s);i++){
     
		if( s[i]==' '||s[i]=='0')
		continue;
		if( s[i]=='1'&&s[i+1]=='0'){
     
		bag[cnt++]=10;
		continue;
	    }
		if( s[i]=='A'){
     
			bag[cnt++]=1;
			continue;
		}
		if( s[i]=='K'||s[i]=='Q'||s[i]=='J'||s[i]=='S'){
     
			bag[cnt++]=10;
			continue;
		}
		bag[cnt++]=s[i]-'0';
	}
	dfs( 1,0 );
	if( flag==0 ){
     
		printf("so sad!");
	
	}else{
     
		
		if( max0==100 )
		printf("so cool!");
		else
		printf("max0");
	}
	
	return 0;
}

7.试题G：JM boy 去爬山 18’
描述
疫情终于终于得到了一定的控制~
JM boy在家宅了又宅，宅了又宅，总算是可以带上口罩出去爬山运动了~
JM boy在爬完山之后，发现自己爬的山像及了一个数列。山是有山峰山谷的，而数列也是可以定义山峰山谷的。
例如，对于某n个数的一种排列，如果不存在任意的i使得
Ai>Ai+1 JM boy想知道，对于1……n的n个数的数列，该数列有多少种排列是属于山峰排列的。
当然，对于n=1及n=2的情况，肯定是所有的排列都属于山峰排列了。
输入
输入一个整数n，表示数列元素的个数。
输出
输出山峰排列的个数。
样例
输入
复制
1
输出
复制
1
输入
复制
3
输出
复制
4
提示
【样例2解释】
共有以下4种方案： 123、132、231、321
【数据规模】
对于60%的数据 n <= 10
对于100%的数据 n <= 60
答案：思路一：
对于小数据60%，直接全排列所有方案，然后再逐一判断每一种方案的是否满足条件~
打印出<=10数据，可以发现，答案为2^{n-1}
思路二：
假设山峰数字为x,除了x的所有的数字，都有两种选择，要么x的左边，要么在x的右边，确定左右之后，所有数字的排列固定，显然答案为2^{n-1}。

代码（C实现）：

#include
typedef  long long ll;
int read(){
     
	int f = 1;
	int x = 0;
	char ch = getchar();
	while( ch <'0' || ch>'9'){
     
		if( ch == '-')
		   f = -1;
		ch = getchar();
	}
	while( ch >='0' && ch<='9'){
     
		x = x*10 + ( ch - '0');
		ch = getchar();
	}
	return x;
} 
int main(){
     
	int n;
	n = read();
	if(n == 1){
     
		printf("1\n");
		return 0;
	}
	ll ans = 1;
	for(int i = 2; i <= n; i++)
	    ans *= 2;
	printf("%lld\n",ans);
	return 0;
}

8.试题H：宝剑锋从磨砺出 20’
描述
幸运的wlxsq偶得一块上古神铁！wlxsq决定将其锻造成一把攻击力不小于K的神器！
wlxsq跋山涉水，耗费巨资请来了锻造大师JM boy，在JM boy的手上，任何材料都能发挥到最大价值~
wlxsq同样耗费巨资提前准备了N个材料。每一次对上古神铁进行锻造都需要选择一个材料配合进行锻造。对于每一个材料i，有两种方式能够配合上古神铁进行锻造：
1、材料i作为辅助，配合三味真火进行锻造，可增加攻击力P1​，材料i可重复使用。
2、材料i直接和上古神铁融合，增加攻击力P2，融合后材料i则不能再被使用了。
由于锻造大师JM boy锻造神器是通过锻造次数来收取费用的。由于wlxsq之前的耗费巨资，导致现在wlxsq资金紧张，wlxsq想知道，他最少需要请JM boy锻造几次，才能够把锻造出攻击力不小于K的一把神兵利器，你能帮帮wlxsq吗？
输入
第一行输入两个整数
N，K，分别表示材料的个数以及攻击力K。
接下来输入N行，每行两个数
Pi1,Pi2,表示每个材料对应的方式1，方式2所能够代来的攻击力提升。
输出
输出最少锻造次数
样例
输入
复制
1 10
3 5
输出
复制
3
输入
复制
2 10
3 5
2 6
输出
复制
2
提示
【样例1解释】
前两次使用材料1通过方式1进行锻造，第三次使用材料1通过方式2进行锻造。共获得
3+3+5=11攻击力
【样例2解释】
分别使用材料1，材料通过方式2进行锻造，共获得
5+6=11攻击力
【数据规模】
对于100%的数据
N≤10^5,K≤109,1≤P1≤P2≤10^9
**答案：考虑贪心。
答案一定是选一些方式1和一些方式2构成的。
那么如果确定了选择方式1和方式2的个数，那么我们一定会选择方式1中权值最大的那个值，以及方式2中权值前k的值之和。
所以，我们将所有方式1从大到小排序，所有方式2从大到小排序。
枚举即可。
复杂度O(nlogn)
**
代码（C++实现）：

#include
using namespace std;

typedef struct{
     
	int v;
	int now;
}node;

node p[200005];

bool cmp(node a,node b){
     
	return a.v > b.v ;
}

int main(){
     
	int n,k;
	scanf("%d %d",&n,&k);
	for(int i = 0; i < n; i++){
     
		scanf("%d %d",&p[2*i].v,&p[2*i+1].v);
		p[2*i].now = 0;
		p[2*i+1].now = 1;
	}
	sort(p, p + 2*n, cmp);
	int i = 0;
	int ans = 0;
	while( k > 0){
     
		if(p[i].now == 1){
     
			k -= p[i].v ;
			i++;
			ans++;
		}
		else{
     
			ans += k / p[i].v ;
			if( k % p[i].v != 0) ans++;
			k = 0;
		}
	}
	printf("%d\n",ans);
	return 0;
}

9.由于疫情缘故，wlxsq家里还剩下超多年货，没有吃完。
为了简化问题，假设wlxsq家里还剩N种年货，每种年货Ai包，同一种年货中每一包都是一样的。
现在wlxsq准备返杭了，他想从N种年货中挑不超过K包年货带返杭。wlxsq想知道他总共有多少种选择方案？
输入
第一行输入两个整数N，K，含义如题目描述。
第二含输入N个整数 Ai，表示每一种年货的数量。
输出
输出总共方案数，结果对998244353取模。
样例
输入
复制
3 1
2 2 2
输出
复制
4
输入
复制
8 13
1 2 3 4 5 6 7 8
输出
复制
65044
提示
【样例1解释】
总共有4种方案，对应每一种年货的选择如下：(1,0,0),(0,1,0),(0,0,1),(0,0,0)
【评测用例规模与约定】
对于40%的数据，2<=N<=10,
对于100%的数据，2<=N<=1000，Ai,K<=10^5
答案：

能力有限，代码不会

10.试题J：梅深不见冬25’
描述
Let’s have some music~
结合音乐做此题，效果更佳~
《梅深不见冬》
风，吹起梅岭的深冬；霜，如惊涛一样汹涌；雪，飘落后把所有烧成空，
像这场，捕捉不到的梦。
醒来时已是多年之久，宫门铜环才长了铁锈，
也开始生出离愁。
——银临《梅深不见冬》

wlxsq在深冬的梅岭中走着，感到十分寒冷，也感到十分孤独。这时他看到前方有一座小屋，透过窗户，他看见里面有一座火炉，如图：

正巧，屋内的主人在家里。wlxsq想要进屋内暖和暖和。于是，他敲了敲门，主人热情的开了门。
wlxsq：您好，我能进您屋内取取暖吗？
主人：好的。但是我有一个条件。
wlxsq：什么条件？

思路：

能力有限，代码不会！！！