Codeforces Round #698 (Div. 2)部分题解(A,B,C,D)
oj: CodeForces
叙述采用倒叙。
D. Nezzar and Board
oj: CodeForces
题意
现有 n n n 个不同的数字组成的数组 a a a 和一个整数 k k k,你可以执行一下操作任意次:
选择两个任意的数字 x x x 和 y y y,然后把 2 x − y 2x-y 2x−y 加入数组a。
问你能否通过有限次的操作使得 k k k 被包含在数组 a a a 里。
题解
我们推理一下这个操作的本质。
2 x − y 2x-y 2x−y 其实就是 x + x − y x+x-y x+x−y,也就是 x x x 加上 x x x 和 y y y 的差值,这个差值可以是正的也可以是负的。执行完之后我们可以对新的数字继续增加这个差值,所以我们就可以根据两个数字得出一个等差数列。数列内的数字都可以倍包含在数组 a a a 里。
难点在于选择不同的数字可以得出不同的等差数列,这些数列中我们可能可以选择两个相距更近的数得出一个更小的差值,进而得到一个更密集的数列。
其实这个问题也不难想,当两个等差数列放到一起时,它们的元素之间相距的最近距离就是两个数列的差值的最大公因数。
假设 a a a 数组是2,6,12
从数组 a a a 中选出 x = 2 , y = 6 x=2,y=6 x=2,y=6,我们可以递推得到 2,6,10,14 等等。这个数列的公差是4。
然后再选出 x = 6 , y = 12 x=6,y=12 x=6,y=12,我们可以递推得到0,6,12,18等等。这个数列的公差是6。
把这两个数列合并,然后找到两个相距最近的点,可以发现2和0,或者10和12,或者12和14。总之此时最近的距离是2,刚好是两个公差的最大公因数gcd(4,6)。我们就可以利用这个最近距离来构造更紧密的等差数列。比如从新的数组 a a a 中选出 x = 0 , y = 2 x=0,y=2 x=0,y=2,就可以构造出0,2,4,6了。
倘若 k k k 等于4,那么在得到2这个公差之前是没办法直接得到4的,现在通过公差2可以由2(原 a a a 数组中的2)+2(公差)=4获得。
而我们的目的是找出一个最小的差值 d d d,然后分别比对每一个 a i a_i ai 看是否可以由 a i a_i ai 和若干个 d d d 得到 k k k。
也不难想,只需要先对 a a a 数组排个序,然后对所有的 a i − a i − 1 a_i-a_{i-1} ai−ai−1 求最大公因数,就得出了那个最小的差值 d d d。
代码
#include C. Nezzar and Symmetric Array
oj: CodeForces
题意
a a a 数组是一个由 2 n 2n 2n 个互不相同的整数组成的数组,且每个 a i a_i ai 都能找到一个 a j a_j aj 满足 a i = − a j a_i=-a_j ai=−aj。 d d d 数组是 d i = ∑ j = 1 2 n ∣ a i − a j ∣ d_i=∑^{2n}_{j=1}|a_i−a_j| di=∑j=12n∣ai−aj∣。
给出一组 d d d,问是否可以构造出一组合法的 a a a 数组。
题解
首先对 d d d 数组排序,然后检查是否每个数字都出现偶数次。因为 a a a 数组是对称出现的,所以 d d d 数组也应该是对称出现的。之后我们每隔一位元素取出一个数字,这样就取出n个数字组成新的 d d d 数组。
假设有这样一组 a a a:
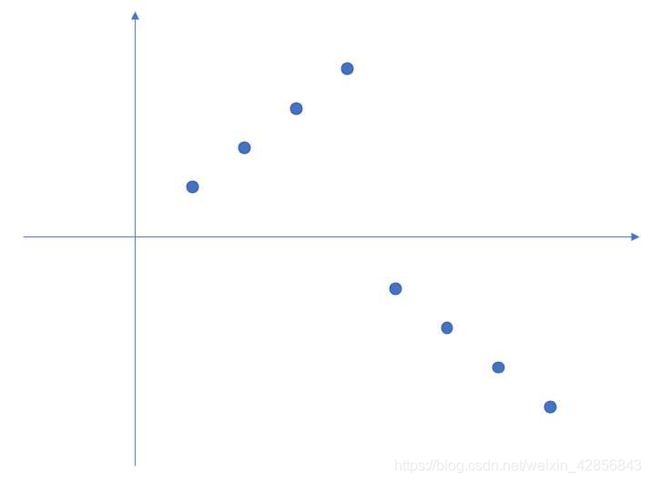
那么 a 0 a_0 a0 对应的 d 0 d_0 d0 其实就是 ∑ i = 1 n ∣ a i ∣ \sum_{i=1}^{n}{|a_i|} ∑i=1n∣ai∣。
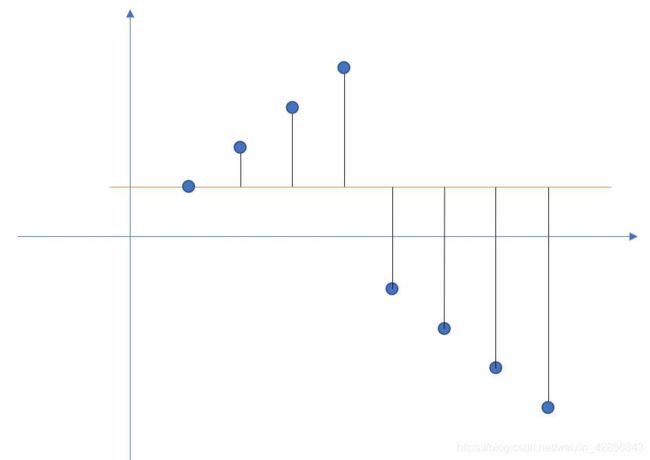
而 a 1 a_1 a1 对应的 d 1 d_1 d1 就有意思了。我们可以借 d 1 − d 0 d_1-d_0 d1−d0 求出 a 1 − a 0 a_1-a_0 a1−a0。
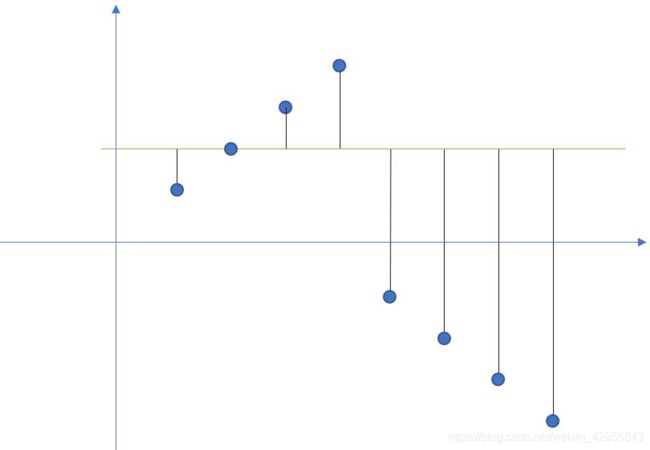
对比 d 0 d_0 d0 的图,会发现其实 d 1 − d 0 = 2 ( a 1 − a 0 ) d_1-d_0=2(a_1-a_0) d1−d0=2(a1−a0)
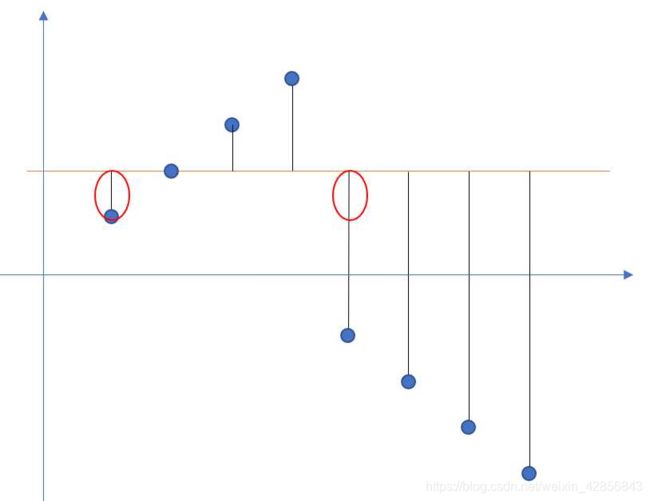
同理可以发现 d 2 − d 1 = 4 ( a 2 − a 1 ) d_2-d_1=4(a_2-a_1) d2−d1=4(a2−a1), d 3 − d 2 = 6 ( a 3 − a 2 ) d_3-d_2=6(a_3-a_2) d3−d2=6(a3−a2)。以此类推。
再配合上文高亮部分,假设 a 0 a_0 a0 为 x x x,我们就可以列出一个 x x x 的方程,方程有解且解不为0(两个0就相等了,而 a a a 数组互不相等)就说明存在合法的 a a a。
x + x + d 1 − d 0 2 + x + d 2 − d 1 4 ⋯ + x + d n − 1 − d n − 2 2 ( n − 1 ) = d 0 2 x+x+\frac{d_1-d_0}{2}+x+\frac{d_2-d_1}{4}\cdots +x+\frac{d_{n-1}-d{n-2}}{2(n-1)}=\frac{d_0}{2} x+x+2d1−d0+x+4d2−d1⋯+x+2(n−1)dn−1−dn−2=2d0
感谢Tryna1大佬纠正错误
剩下的就是各种整除和不为0的判断了。
代码
#include B. Nezzar and Lucky Number
oj: CodeForces
题意
给你一个 d d d, q q q 次询问一个数字 a a a 是否可以由若干个数字相加得到且这些数字的数位中都含有 d d d 这个数字。
题解
当 a < 10 d a<10d a<10d 时,假设 a a a 的个位数字是 x x x,那么需要找到一个最小的个数 n n n 使得 n d ≡ x ( m o d 10 ) nd\equiv x(mod\ 10) nd≡x(mod 10) 如果这时 a ≥ n d a\ge nd a≥nd,那么我们就可以构造一组 d , d , ⋯ , d ⏟ n − 1 , a − ( n − 1 ) d \underbrace{ d,d,\cdots,d }_{n-1},a-(n-1)d n−1 d,d,⋯,d,a−(n−1)d,其中所有的数字的个位数字都是 d d d。那么我们只需要检查是否可以找到一个 n n n 使得 n d ≡ x ( m o d 10 ) nd\equiv x(mod\ 10) nd≡x(mod 10) 同时 a ≥ n d a\ge nd a≥nd。
当 10 d ≤ a < 20 d 10d\le a< 20d 10d≤a<20d 时,找到一个 x x x 满足 a − 10 d − x ≡ 0 ( m o d d ) a-10d-x\equiv 0(mod\ d) a−10d−x≡0(mod d), x x x 可以取 0 0 0。那么就相当于构造了一组 10 d + x , d , d , ⋯ , d ⏟ a − 10 d − x d 10d+x,\underbrace{ d,d,\cdots,d }_{\frac{a-10d-x}{d}} 10d+x,da−10d−x d,d,⋯,d,其中第一个数字的十位是 d d d,其余数字的个位都是 d d d。也就是说当 10 d ≤ a < 20 d 10d\le a< 20d 10d≤a<20d 时都可以构造出一组合法的解。
当 a ≥ 20 d a\ge 20d a≥20d 时我们先让 a a a 减去若干个 10 d 10d 10d,使得 a a a 满足 10 d ≤ a < 20 d 10d\le a< 20d 10d≤a<20d,那么问题就回到了情况2。所以此时也是都有解的。
代码
#include A. Nezzar and Colorful Balls
oj: CodeForces
题意
n个数字组成一个不严格的递增序列,你需要给每个数字染色,以便所有颜色相同的数字的值都不一样,求出最小的颜色数目。
题解
考虑出现次数最多的数字,由于需要给它们分配不同的颜色,所以出现的次数就是需要的颜色数目。
代码
#include