php 数据结构 对象结构_PHP开发人员的数据结构：堆

php 数据结构 对象结构

In past couple articles I’ve introduced you to three basic data structures: stack, queue, and tree. In this article I’ll introduce you to another abstract data type that is closely related: heap. Heaps are specialized tree-like data structures which satisfy the heap property – the node value (key) of any parent is always ordered with respect to its child node values across the entire tree. Let’s take a closer look!

在过去的几篇文章中，我向您介绍了三种基本的数据结构： stack，queue和tree 。 在本文中，我将向您介绍另一种密切相关的抽象数据类型：堆。 堆是满足堆属性的特殊树状数据结构，即，任何父节点的节点值(键)始终相对于整个树中的子节点值进行排序。 让我们仔细看看！

堆 (Heaps)

There are several heap variants. For instance, if parent keys are ordered such that they are of equal or greater value than their children, and the highest key is at the root, the heap is said to be a maxheap. If parent keys are ordered such that they are of equal or lower value than their children, with the lowest key at the root, the heap is called a minheap. SPL (PHP>=5.3.0) provides a basic heap, minheap, maxheap, and a specialized data type called a Priority Queue.

有几种堆变体。 例如，如果父键的排序使得它们的值等于或大于子键的值，并且最高的键位于根，则堆被称为maxheap 。 如果排序父键的值等于或低于子键的值，且最低键在根，则堆称为minheap 。 SPL(PHP> = 5.3.0)提供基本的堆，minheap，maxheap和称为“优先级队列”的特殊数据类型。

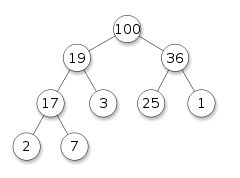
So here’s an example of what a heap looks like:

因此，这是一个堆的示例：

The figure above depicts a complete binary maxheap. It’s binary because each node has exactly two children, and a maxheap because the highest value key is at the root node and all parent nodes have values greater than their children.

上图描述了完整的二进制maxheap。 之所以是二进制的，是因为每个节点恰好有两个子节点，而maxheap是因为最高值键在根节点且所有父节点的值都大于其子节点。

While heaps are usually implemented as complete binary trees, unlike binary trees there is no implied ordering of siblings and cousins, nor is there any implied sequence for an in-order traversal.

尽管通常将堆实现为完整的二叉树，但与二叉树不同的是，没有隐含的同级和表亲排序，也没有隐含的顺序遍历顺序。

Heaps are a variant of the table data type so they also have the same basic operations:

堆是表数据类型的变体，因此它们也具有相同的基本操作：

• create – create an empty heap.

  创建 –创建一个空堆。

• isEmpty – determine if the heap is empty.

  isEmpty –确定堆是否为空。

• insert – add an item to the heap.

  insert –将一个项目添加到堆中。

• extract – remove the topmost item (root) item from the heap.

  提取 –从堆中删除最顶层的项目(根)项目。

Unlike a table, the retrieve and delete operations for a heap are combined into a single extract operation, so let’s focus on how the extract operation works first.

与表不同，堆的检索和删除操作被合并到单个提取操作中，因此让我们集中讨论提取操作首先如何工作。

The condition for removing an item from the heap is that we can only remove the root node. Let’s say we removed the root node (100) from the above example. We would be left with two disjoint heaps. We need a method of transforming the remaining nodes back into a single heap after the root is removed. Joining them is easily accomplished by moving the last node to the root, but we’re left with a resulting structure that fails the heap property. Such a structure is called a semiheap.

从堆中删除项目的条件是我们只能删除根节点。 假设我们从上面的示例中删除了根节点(100)。 我们将剩下两个不相交的堆。 我们需要一种方法，在删除根之后将其余节点转换回单个堆。 通过将最后一个节点移到根节点可以很容易地实现它们的连接，但是剩下的结果结构使heap属性失效。 这样的结构称为半堆 。

We now need a way to transform the semiheap into a heap. One strategy is to trickle the root item down the tree until it reaches a node where it will not be out of place. We iteratively compare the value of the root node to its children and swap places with the larger child until it arrives at a node where no child has a greater (or equal) value than itself.

现在，我们需要一种将半堆转换为堆的方法。 一种策略是将根项滴入树中，直到其到达不会错位的节点为止。 我们迭代比较根节点与其子节点的值，并与较大的子节点交换位置，直到它到达一个节点，在该节点中，没有一个子节点具有比其更大(或相等)的值。

将堆实现为数组 (Implementing a Heap as an Array)

We can naively implement a binary maxheap as an array. A binary bode has at most two children, therefore for any n number of nodes a binary heap will have at most 2n + 1 nodes.

我们可以天真地将二进制maxheap实现为数组。 二进制波德最多有两个子代，因此，对于任何n个节点，二进制堆最多具有2n +1个节点。

Here’s what an implementation looks like:

这是实现的样子：

heap  = array();
    }

    public function isEmpty() {
        return empty($this->heap);
    }

    public function count() {
        // returns the heapsize
        return count($this->heap) - 1;
    }

    public function extract() {
        if ($this->isEmpty()) {
            throw new RunTimeException('Heap is empty');
        }

        // extract the root item
        $root = array_shift($this->heap);

        if (!$this->isEmpty()) {
            // move last item into the root so the heap is
            // no longer disjointed
            $last = array_pop($this->heap);
            array_unshift($this->heap, $last);

            // transform semiheap to heap
            $this->adjust(0);
        }

        return $root;
    }

    public function compare($item1, $item2) {
        if ($item1 === $item2) {
            return 0;
        }
        // reverse the comparison to change to a MinHeap!
        return ($item1 > $item2 ? 1 : -1);
    }

    protected function isLeaf($node) {
        // there will always be 2n + 1 nodes in the
        // sub-heap
        return ((2 * $node) + 1) > $this->count();
    }

    protected function adjust($root) {
        // we've gone as far as we can down the tree if
        // root is a leaf
        if (!$this->isLeaf($root)) {
            $left  = (2 * $root) + 1; // left child
            $right = (2 * $root) + 2; // right child

            // if root is less than either of its children
            $h = $this->heap;
            if (
              (isset($h[$left]) &&
                $this->compare($h[$root], $h[$left]) < 0)
              || (isset($h[$right]) &&
                $this->compare($h[$root], $h[$right]) < 0)
            ) {
                // find the larger child
                if (isset($h[$left]) && isset($h[$right])) {
                  $j = ($this->compare($h[$left], $h[$right]) >= 0)
                      ? $left : $right;
                }
                else if (isset($h[$left])) {
                  $j = $left; // left child only
                }
                else {
                  $j = $right; // right child only
                }

                // swap places with root
                list($this->heap[$root], $this->heap[$j]) = 
                  array($this->heap[$j], $this->heap[$root]);

                // recursively adjust semiheap rooted at new
                // node j
                $this->adjust($j);
            }
        }
    }
}

The insertion strategy is the exact opposite of extraction: we insert the item at the bottom of the heap and trickle it up to its correct location. Since we know that a complete binary tree with a full last level contains n/2 + 1 nodes, we can traverse the heap using a simple binary search.

插入策略与提取完全相反：我们将项目插入堆的底部，然后将其滴流到正确的位置。 由于我们知道具有完整最后一级的完整二进制树包含n / 2 + 1个节点，因此我们可以使用简单的二进制搜索遍历堆。

public function insert($item) {
    // insert new items at the bottom of the heap
    $this->heap[] = $item;

    // trickle up to the correct location
    $place = $this->count();
    $parent = floor($place / 2);
    // while not at root and greater than parent
    while (
      $place > 0 && $this->compare(
        $this->heap[$place], $this->heap[$parent]) >= 0
    ) {
        // swap places
        list($this->heap[$place], $this->heap[$parent]) =
            array($this->heap[$parent], $this->heap[$place]);
        $place = $parent;
        $parent = floor($place / 2);
    }
}

So let’s see what happens when we insert a few items into the structure:

因此，让我们看看将一些项目插入结构时会发生什么：

insert(19);
$heap->insert(36);
$heap->insert(54);
$heap->insert(100);
$heap->insert(17);
$heap->insert(3);
$heap->insert(25);
$heap->insert(1);
$heap->insert(67);
$heap->insert(2);
$heap->insert(7);

If you dump the heap structure you’ll notice that the items aren’t in any particular order. In fact, it’s not even in the order we would expect:

如果转储堆结构，您会注意到这些项目的顺序不是特定的。 实际上，它甚至没有达到我们期望的顺序：

Array
(
    [0] => 100
    [1] => 67
    [2] => 54
    [3] => 36
    [4] => 19
    [5] => 7
    [6] => 25
    [7] => 1
    [8] => 17
    [9] => 2
    [10] => 3
)

However, if you extract the items, this is what you would get:

但是，如果您提取项目，则将得到以下结果：

isEmpty()) {
    echo $heap->extract() . "n";
}

100
67
54
36
25
19
17
7
3
2
1

SplMaxHeap和SplMinHeap (SplMaxHeap and SplMinHeap)

Fortunately for us, SplHeap, SplMaxHeap and SplMinHeap abstracts all of this for us. All we have to do is extend the base class and override the comparison method like so:

对我们来说幸运的是，SplHeap，SplMaxHeap和SplMinHeap为我们提供了所有这些摘要。 我们要做的就是扩展基类并覆盖比较方法，如下所示：

The compare method can perform any arbitrary comparison, as long as it returns – in the case of a SplMaxHeap – a positive integer if $item1 is greater than $item2, 0 if they are equal, or a negative integer otherwise. If extending SplMinHeap, it should instead return a positive integer if $item1 is less than $item2.

compare方法可以执行任何任意比较，只要它返回(对于SplMaxHeap)，则当$item1大于$item2为正整数，如果相等$item2 0，否则返回负整数。 如果扩展SplMinHeap，则应在$item1小于$item2返回正整数。

It’s not recommended to have multiple elements with the same value in a heap as they may end up in an arbitrary relative position.

不建议在堆中包含多个具有相同值的元素，因为它们最终可能位于任意相对位置。

SplPriorityQueue (SplPriorityQueue)

The Priority Queue is a specialized abstract data type that behaves like a queue, but is usually implemented as a heap – in the case of SplPriorityQueue, as a maxheap. Prioritized queues have many real-world applications, such as service desks/ticket escalation. They are also essential in improving the performance of certain graph applications.

Priority Queue是一种特殊的抽象数据类型，其行为类似于队列，但通常实现为堆(在SplPriorityQueue的情况下，作为maxheap)。 优先队列具有许多实际应用程序，例如服务台/票务升级。 它们对于提高某些图形应用程序的性能也至关重要。

Like the SplHeap, you only have to override the base class and comparator method:

像SplHeap一样，您只需要重写基类和比较器方法即可：

The main difference in a SplPriorityQueue is that the insert operation expects a priority value – which can be a mixed data type. The insert operation uses the priority to sift the element up the heap based on the returned result of your comparator.

SplPriorityQueue的主要区别在于插入操作需要一个优先级值-可以是混合数据类型。 插入操作使用优先级根据比较器返回的结果在堆中筛选元素。

For illustration purposes, let’s use integer priorities:

出于说明目的，让我们使用整数优先级：

insert('A', 4);
$pq->insert('B', 3);
$pq->insert('C', 5);
$pq->insert('D', 8);
$pq->insert('E', 2);
$pq->insert('F', 7);
$pq->insert('G', 1);
$pq->insert('H', 6);
$pq->insert('I', 0);
 
while ($pq->valid()) {
    print_r($pq->current());
    echo "n";
    $pq->next();
}

I
G
E
B
A
C
H
F
D 

Notice that our items are displayed in order of priority – highest to lowest (the lower the value, the higher the priority). You can reverse the priority order by changing the comparator to return a positive integer if $p1 is greater than $p2.

请注意，我们的项目按优先级顺序显示-从高到低(值越低，优先级越高)。 如果$p1大于$p2则可以通过更改比较器以返回正整数来反转优先级顺序。

By default, only the element’s data is extracted. If you wanted to extract the priority values only, or both the data and priority, you can set the extract flag like this:

默认情况下，仅提取元素的数据。 如果只想提取优先级值，或者数据和优先级都提取，则可以这样设置提取标志：

setExtractFlags(SplPriorityQueue::EXTR_PRIORITY);

// extract both data and priority (returns an associative
// array for each element)
$pq->setExtractFlags(SplPriorityQueue::EXTR_BOTH);

摘要 (Summary)

I’ve introduced you to the heap abstract data type and showed you how items are inserted and extracted from a heap using a simple array implementation. We’ve also seen how the comparator is used in min and maxheaps, and how the Priority Queue operates. Stay tuned; in the next article I’ll discuss graphs!

我已经向您介绍了堆抽象数据类型，并向您展示了如何使用简单的数组实现从堆中插入和提取项目。 我们还看到了如何在min和maxheap中使用比较器，以及Priority Queue的工作方式。 敬请关注; 在下一篇文章中，我将讨论图形！

Image via Fotolia

图片来自Fotolia

翻译自: https://www.sitepoint.com/data-structures-3/

php 数据结构 对象结构