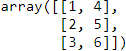LIQING LIN

cp10_回归预测连续目标变量_boston_Residual_plot_mlxtend_sns_pd_covariance_correlation_RANSAC_R2_Ridge_C_F_A_K_树

Predicting Continuous Target Variables with Regression Analysis

Throughout the previous https://blog.csdn.net/Linli522362242/article/details/110740856(cp9_Embedding a Model into a Web Application_pickle_sqlite3_Flask_wtforms_pythonanywhere_pickle_serialization), you learned a lot about the main concepts behind supervised learning and trained many different models for classification tasks to predict group memberships or categorical variables. We will dive into another subcategory of supervised learning: regression analysis.

Regression models are used to predict target variables on a continuous scale, which makes them attractive for addressing many questions in science. They also have applications in industry, such as understanding relationships between variables, evaluating trends, or making forecasts. One example is predicting the sales of a company in future months.

In this chapter, we will discuss the main concepts of regression models and cover the following topics:
• Exploring and visualizing datasets
• Looking at different approaches to implement linear regression models
• Training regression models that are robust to outliers
• Evaluating regression models and diagnosing common problems
• Fitting regression models to nonlinear data

Introducing linear regression

The goal of linear regression is to model the relationship between one or multiple features and a continuous target variable. In contrast to classification—a different subcategory of supervised learning—regression analysis aims to predict outputs on a continuous scale rather than categorical class labels.

In the following subsections, you will be introduced to the most basic type of linear regression, simple linear regression, and understand how to relate it to the more general, multivariate case (linear regression with multiple features).

Simple linear regression

The goal of simple (univariate) linear regression is to model the relationship between a single feature (explanatory variable, x) and a continuous-valued target (response variable, y). The equation of a linear model with one explanatory variable is defined as follows:

Here, the weight, , represents the y axis intercept and is the weight coefficient of the explanatory variable. Our goal is to learn the weights of the linear equation to describe the relationship between the explanatory variable and the target variable, which can then be used to predict the responses of new explanatory variables that were not part of the training dataset.

Based on the linear equation that we defined previously, linear regression can be understood as finding the best-fitting straight line through the training examples, as shown in the following figure:
https://blog.csdn.net/Linli522362242/article/details/104005906
This best-fitting line is also called the regression line, and the vertical lines from the regression line to the training examples are the so-called offsets or residuals—the errors of our prediction.

Multiple linear regression

The previous section introduced simple linear regression, a special case of linear regression with one explanatory variable. Of course, we can also generalize the linear regression model to multiple explanatory variables; this process is called multiple linear regression:

Here, is the y axis intercept with = 1.

The following figure shows how the two-dimensional, fitted hyperplane of a multiple linear regression model with two features could look:

As you can see, visualizations of multiple linear regression hyperplanes in a three-dimensional scatterplot are already challenging to interpret when looking at static figures. Since we have no good means of visualizing hyperplanes with two dimensions in a scatterplot (multiple linear regression models fit to datasets with three or more features), the examples and visualizations in this chapter will mainly focus on the univariate case, using simple linear regression. However, simple and multiple linear regression are based on the same concepts and the same evaluation
techniques; the code implementations that we will discuss in this chapter are also compatible with both types of regression model.

Exploring the Housing dataset

Before we implement the first linear regression model, we will discuss a new dataset, the Housing dataset, which contains information about houses in the suburbs of Boston collected by D. Harrison and D.L. Rubinfeld in 1978. The Housing dataset has been made freely available and is included in the code bundle of this book. The dataset has recently been removed from the UCI Machine Learning Repository but is available at (from tensorflow.keras.datasets import boston_housing 10_Introduction to Artificial Neural Networks w Keras1_HuberLoss_astype_dtype_DNN_MLP_G.gv.pdf_EMA https://blog.csdn.net/Linli522362242/article/details/106433059 OR https://blog.csdn.net/Linli522362242/article/details/106755312) or scikit-learn (https://github.com/scikit-learn/scikit-learn/blob/master/sklearn/datasets/data/boston_house_prices.csv). As with each new dataset, it is always helpful to explore the data through a simple visualization, to get a better feeling of what we are working with.

Loading the Housing dataset into a data frame

In this section, we will load the Housing dataset using the pandas read_csv function, which is fast and versatile and a recommended tool for working with tabular data stored in a plaintext format.

The features of the 506 examples in the Housing dataset have been taken from the original source that was previously shared on https://archive.ics.uci.edu/ml/datasets/Housing and summarized here:

• CRIM: Per capita crime rate by town 城镇人均犯罪率
• ZN: Proportion of residential land zoned for lots over 25,000 sq. ft. 占地远超过25,000平方英尺的住宅用地比例
• INDUS: Proportion of non-retail business acres['eɪkəs]英亩 per town 每个镇非零售业务用地比例
• CHAS: Charles River dummy variable (= 1 if tract bounds束缚 river and 0 otherwise如果房屋位于河边则值为1，否则为0)

If a qualitative predictor定性预测因子 (also known as a factor) only has two levels, or possible values, then incorporating it into a regression model is very simple. We level simply create an indicator or dummy variable that takes on two possible numerical values. For example, based on the gender variable, we can create variable a new variable that takes the form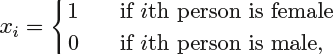

• NOX: Nitric oxide concentration (parts per 10 million) 一氧化氮浓度(每千万分之一)
• RM: Average number of rooms per dwelling[ˈdwelɪŋ]住宅
• AGE: Proportion of owner-occupied units自住单元 built prior to 1940
• DIS: Weighted distances to five Boston employment centers
• RAD: Index of accessibility to radial highways 径向公路通达性指数
• TAX: Full-value property tax rate per $10,000 每10,000美元的全值财产税率
• PTRATIO: Pupil-teacher ratio by town 各镇师生比例
• B: 1000*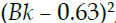, where Bk is the proportion of [people of African American descent血统] by town
• LSTAT: Percentage of lower status地位 of the population
• MEDV: Median value of owner-occupied homes in $1000s 自住房的中位数价值（以1000美元计）

For the rest of this chapter, we will regard the house prices (MEDV) as our target variable—the variable that we want to predict using one or more of the 13 explanatory variables. Before we explore this dataset further, let's load it into a pandas DataFrame:
https://raw.githubusercontent.com/scikit-learn/scikit-learn/master/sklearn/datasets/data/boston_house_prices.csv

import pandas as pd

df = pd.read_csv('https://raw.githubusercontent.com/scikit-learn/scikit-learn/master/sklearn/datasets/data/boston_house_prices.csv',
                 header=1,
                 sep=',')
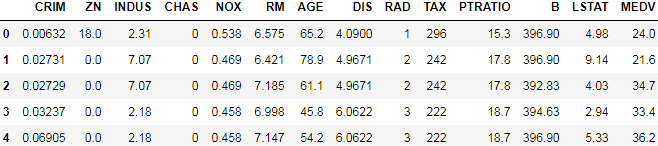
df.head()

To confirm that the dataset was loaded successfully, we can display the first five lines of the dataset, as shown in the following figure:

df.columns

Index(['CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', 'DIS', 'RAD', 'TAX', 'PTRATIO', 'B', 'LSTAT', 'MEDV'],
dtype='object')

Visualizing the important characteristics of a dataset

Exploratory data analysis (EDA) is an important and recommended first step prior to the training of a machine learning model. In the rest of this section, we will use some simple yet useful techniques from the graphical EDA toolbox that may help us to visually detect the presence of outliers, the distribution of the data, and the relationships between features.

First, we will create a scatterplot matrix that allows us to visualize the pair-wise correlations between the different features in this dataset in one place. To plot the scatterplot matrix, we will use the scatterplot matrix function from the MLxtend library (http://rasbt.github.io/mlxtend/), which is a Python library that contains various convenience functions for machine learning and data science
applications in Python.

You can install the mlxtend package via conda install mlxtend or pip install mlxtend(https://blog.csdn.net/Linli522362242/article/details/108037567). After the installation is complete, you can import the package and create the scatterplot matrix as follows:

mlxtend.plotting VS seaborn VS pandas.plotting

import matplotlib.pyplot as plt
from mlxtend.plotting import scatterplotmatrix

cols = ['LSTAT', # Percentage of lower status of the population
        'INDUS', # Proportion of non-retail business acres per town 
        'NOX',   # Nitric oxide concentration (parts per 10 million)
        'RM',    # Average number of rooms per dwelling
        'MEDV']  # Median value of owner-occupied homes in $1000s

scatterplotmatrix( df[cols].values, figsize=(10,8), names=cols, alpha=0.5 )
plt.tight_layout()

plt.show()

As you can see in the following figure, the scatterplot matrix provides us with a useful graphical summary of the relationships in a dataset:

mlxtend.plotting VS seaborn VS pandas.plotting

Using this scatterplot matrix, we can now quickly eyeball how the data is distributed and whether it contains outliers. For example, we can see that there is a linear relationship between RM and the housing prices MEDV (the fifth column of the fourth row)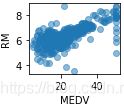. Furthermore, we can see in the histogram (the lower right subplot in the scatter plot matrix) that the MEDV variable seems to be normally distributed but contains several outliers.

####################################

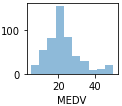Normality assumption of linear regression

Note that in contrast to common belief, training a linear regression model does not require that the explanatory or target variables are normally distributed. The normality assumption is only a requirement for certain statistics and hypothesis tests that are beyond the scope of this book (for more information on this topic, please refer to Introduction to Linear Regression Analysis, Montgomery, Douglas C. Montgomery, Elizabeth A. Peck, and G.Geoffrey Vining, Wiley, 2012, pages: 318-319).
####################################

Figure 2-14 shows various plots along with the correlation coefficient between their horizontal and vertical axes https://blog.csdn.net/Linli522362242/article/details/103387527

import matplotlib.pyplot as plt
import seaborn as sns

cols = ['LSTAT', # Percentage of lower status of the population
        'INDUS', # Proportion of non-retail business acres per town 
        'NOX',   # Nitric oxide concentration (parts per 10 million)
        'RM',    # Average number of rooms per dwelling
        'MEDV']  # Median value of owner-occupied homes in $1000s

sns.set( style='whitegrid', context='notebook')
sns.pairplot( df[cols], height=2.0)
plt.show()

Due to space constraints and in the interest of readability, we have only plotted five columns from the dataset: LSTAT, INDUS, NOX, RM, and MEDV. However, you are encouraged to create a scatterplot matrix of the whole DataFrame to explore the dataset further by choosing different column names in the previous scatterplotmatrix function call, or including all variables in the scatterplot matrix by omitting the column selector.

######################################################################
Importing the seaborn library modifies the default aesthetics of matplotlib for the current Python session. If you do not want to use seaborn's style settings, you can reset the matplotlib settings
by executing the following command:

sns.reset_orig()

######################################################################

mlxtend.plotting VS seaborn VS pandas.plotting

from pandas.plotting import scatter_matrix
import matplotlib.pyplot as plt

cols = ['LSTAT', # Percentage of lower status of the population
        'INDUS', # Proportion of non-retail business acres per town 
        'NOX',   # Nitric oxide concentration (parts per 10 million)
        'RM',    # Average number of rooms per dwelling
        'MEDV']  # Median value of owner-occupied homes in $1000s

scatter_matrix( df[cols], figsize=(12,10) )
plt.show()

Looking at relationships using a correlation matrix相关系数矩阵

In the previous section, we visualized the data distributions of the Housing dataset variables in the form of histograms and scatterplots. Next, we will create a correlation matrix to quantify量化 and summarize linear relationships between variables https://blog.csdn.net/Linli522362242/article/details/103387527. A correlation matrix is closely related to the covariance matrix that we covered in the section Unsupervised dimensionality reduction via principal component analysis in cp5_Compressing Data via Dimensionality Reduction_feature extraction_PCA_LDA_convergence_kernel PCA https://blog.csdn.net/Linli522362242/article/details/105196037. We can interpret the correlation matrix as being a rescaled version of the covariance matrix. In fact, the correlation matrix is identical to a covariance matrix computed from standardized features.
###########################################################
https://blog.csdn.net/Linli522362242/article/details/105196037

standardize the features(the PCA directions are highly sensitive to data scaling, and we need to standardize the features prior to PCA if the features were measured on different scales and we want to assign equal importance to all features.):

# standardize the features
from sklearn.preprocessing import StandardScaler
 
sc = StandardScaler()
X_train_std = sc.fit_transform(X_train)
X_test_std = sc.transform(X_test)

second step: constructing the covariance matrix. The symmetric d × d -dimensional covariance matrix, where d is the number of dimensions in the dataset, stores the pairwise成对地 covariances between the different features. For example, the covariance协方差 between two features and on the population level can be calculated via the following equation:

Here, and are the sample means of feature j and k , respectively. Note that the sample means are zero if we standardize the dataset. A positive covariance between two features indicates that the features increase or decrease together, whereas a negative covariance indicates that the features vary in opposite directions. For example, a covariance matrix of three features can then be written as (note that stands for the Greek uppercase letter sigma, which is not to be confused with the sum symbol):

The eigenvectors特征向量 of the covariance matrix represent the principal components (the directions of maximum variance ), whereas the corresponding eigenvalues will define their magnitude. In the case of the Wine dataset, we would obtain 13 eigenvectors and eigenvalues from the 13×13 -dimensional covariance matrix.

Now, let's obtain the eigenpairs of the covariance matrix. As we surely remember from our introductory linear algebra or calculus classes, an eigen vector satisfies the following condition:

Here, is a scalar: the eigenvalue(Lagrange multiplier). Since the manual computation of eigenvectors and eigenvalues is a somewhat tedious and elaborate复杂 task, we will use the linalg.eig function from NumPy to obtain the eigenpairs of the Wine covariance matrix:

import numpy as np
 
cov_mat = np.cov(X_train_std.T) #the covariance matrix
eigen_vals, eigen_vecs = np.linalg.eig( cov_mat )
print('\nEigenValues \n%s' % eigen_vals

Using the numpy.cov function, we computed the covariance matrix of the standardized training dataset. Using the linalg.eig function, we performed the eigen decomposition, which yielded a vector (eigen_vals) consisting of 13 eigenvalues and the corresponding eigenvectors stored as columns in a 13 x 13-dimensional matrix (eigen_vecs).

####################

Note

The numpy.linalg.eig function was designed to operate on both symmetric and non-symmetric square matrices. However, you may find that it returns complex（复合） eigenvalues in certain cases.

A related function, numpy.linalg.eigh, has been implemented to decompose Hermetian matrices, which is a numerically more stable approach to work with symmetric matrices such as the covariance matrix; numpy.linalg.eigh always returns real eigenvalues.
###################

Total and explained variance

Since we want to reduce the dimensionality of our dataset by compressing it onto a new feature subspace, we only select the subset of the eigenvectors (principal components) that contains most of the information (variance方差最大). The eigenvalues define the magnitude of the eigenvectors（特征值的大小决定了特征向量的重要性）, so we have to sort the eigenvalues by decreasing magnitude; we are interested in the top k eigenvectors based on the values of their corresponding eigenvalues. But before we collect those k most informative eigenvectors, let us plot the variance explained ratios of the eigenvalues. The variance explained ratio(方差解释比率或者方差贡献率) of an eigenvalue is simply the fraction of an eigenvalue and the total sum of the eigenvalues:

Using the NumPy cumsum function, we can then calculate the cumulative sum of explained variances, which we will then plot via Matplotlib's step function:


tot = sum(eigen_vals) #the total sum of the eigenvalues
var_exp = [ (i/tot) for i in sorted(eigen_vals, reverse=True) ] #The variance explained ratio of an eigenvalue
cum_var_exp = np.cumsum( var_exp ) #the cumulative sum of explained variances
 
import matplotlib.pyplot as plt
 
         #13 eigenvalues
plt.bar( range(1,14), var_exp, alpha=0.5, align="center", label="individual explained variance")
#where="mid": Steps occur half-way between the *x* positions.
plt.step( range(1,14), cum_var_exp, where="mid", label="cumulative explained variance")
plt.ylabel("Explained variance ratio")
plt.xlabel("Principal component index")
plt.legend(loc="best")

The resulting plot indicates that the first principal component alone accounts for approximately 40 percent of the variance. Also, we can see that the first two principal components combined explain almost 60 percent of the variance in the dataset.

Although the explained variance plot reminds us of the feature importance values that we computed in Chapter 4, Building Good Training Sets – Data Preprocessing, via random forests, we should remind ourselves that PCA is an unsupervised method, which means that information about the class labels is ignored. Whereas a random forest uses the class membership information to compute the node impurities, variance measures the spread of values along a feature axis.

Feature transformation

After we have successfully decomposed the covariance matrix into eigenpairs(eigenvector and eigenvalue), let's now proceed with the last three steps to transform the Wine dataset onto the new principal component axes. The remaining steps we are going to tackle in this section are the following ones:

Select k eigenvectors, which correspond to the k largest eigenvalues, where k is the dimensionality of the new feature subspace ( ).
Construct a projection matrix W from the "top" k eigenvectors.
Transform the d-dimensional input dataset X using the projection matrix W to obtain the new k-dimensional feature subspace.

Or, in less technical terms, we will sort the eigenpairs by descending order of the eigenvalues, construct a projection matrix from the selected eigenvectors, and use the projection matrix to transform the data onto the lower-dimensional subspace.

We start by sorting the eigenpairs by decreasing order of the eigenvalues:

# Make a list of (eigenvalue, eigenvector) tuples
eigen_pairs = [ (np.abs(eigen_vals[i]), eigen_vecs[:,i]) for i in range(len(eigen_vals)) ]
eigen_pairs.sort(reverse=True)

Next, we collect the two eigenvectors that correspond to the two largest eigenvalues, to capture about 60 percent of the variance in this dataset. Note that we only chose two eigenvectors for the purpose of illustration, since we are going to plot the data via a two-dimensional scatter plot later in this subsection. In practice, the number of principal components has to be determined by a trade-off between computational efficiency and the performance of the classifier:

eigen_pairs[:2]


#eigen_pairs:[(eigen_value, eigen_vector(array type)),
#             (eigen_value, eigen_vector),...]             
              #eigen_pairs[0][1]: get first eigenvector or first principal component
w = np.hstack((eigen_pairs[0][1][:, np.newaxis],#[:, np.newaxis]:the principal component as 1st column
               eigen_pairs[1][1][:, np.newaxis] #[:, np.newaxis]:the principal component as 2nd column
              )
             )#( ([1st column], [second column]) )
print('Matrix W:\n', w)

By executing the preceding code, we have created a 13 x 2-dimensional projection matrix W from the top two eigenvectors.
#########################################
Note

Depending on which version of NumPy and LAPACK(Linear Algebra PACKage) you are using, you may obtain the matrix W with its signs flipped. Please note that this is not an issue; if v is an eigenvector of a (covariance) matrix , we have:

Here is our eigenvalue, and - is also an eigenvector( and v is a unit vector, note that we are only interested in the direction defined by v) that has the same eigenvalue, since:

#########################################
Using the projection matrix, we can now transform a sample x (represented as a 1 x 13-dimensional row) onto the PCA subspace (the principal components one and two) obtaining , now a two-dimensional sample vector consisting of two new features:

X_train_std[0].dot(w)

Similarly, we can transform the entire 124 x 13-dimensional training dataset onto the two principal components by calculating the matrix dot product:


X_train_pca = X_train_std.dot(w)
X_train_std[:3]

X_train_pca[:3]

cp5_Compressing Data via Dimensionality Reduction_feature extraction_PCA_LDA_convergence_kernel PCA : https://blog.csdn.net/Linli522362242/article/details/105196037

###########################################################

In the previous section, we visualized the data distributions of the Housing dataset variables in the form of histograms and scatterplots. Next, we will create a correlation matrix to quantify量化 and summarize linear relationships between variables https://blog.csdn.net/Linli522362242/article/details/103387527. A correlation matrix is closely related to the covariance matrix that we covered in the section Unsupervised dimensionality reduction via principal component analysis in cp5_Compressing Data via Dimensionality Reduction_feature extraction_PCA_LDA_convergence_kernel PCA https://blog.csdn.net/Linli522362242/article/details/105196037. We can interpret the correlation matrix as being a rescaled version of the covariance matrix. In fact, the correlation matrix is identical to a covariance matrix computed from standardized features.

The correlation matrix相关系数矩阵 is a square matrix that contains the Pearson product-moment correlation coefficient 皮尔逊积矩相关系数 (often abbreviated as Pearson's r), which measures the linear dependence between pairs of features. The correlation coefficients are in the range –1 to 1. Two features have a perfect positive correlation if r = 1, no correlation if r = 0, and a perfect negative correlation if r = –1. As mentioned previously, Pearson's correlation coefficient can simply be calculated as the covariance between two features, x and y (numerator), divided by the product of their standard deviations (denominator):
( Pearson product-moment correlation coefficient )Pearson's r :
# the covariance协方差 between two features and on the population level can be calculated via the following equation
Here, denotes the mean of the corresponding feature, is the covariance between the features x and y, and and are the features' standard deviations.

Covariance versus correlation for standardized features

We can show that the covariance between a pair of standardized features is, in fact, equal to their linear correlation coefficient. To show this, let's first standardize the features x and y to obtain their z-scores, which we will denote as ′ and ′, respectively:

Remember that we compute the (population) covariance between two features as follows:
Since standardization centers a feature variable at mean zero, we can now calculate the covariance between the scaled features as follows:

Through re-substitution( ), we then get the following result:

Finally, we can simplify this equation as follows: ( correlation coefficient formula)

In the following code example, we will use NumPy's corrcoef function on the five feature columns that we previously visualized in the scatterplot matrix, and we will use MLxtend's heatmap function to plot the correlation matrix array as a heat map:

from mlxtend.plotting import heatmap
import numpy as np

cm = np.corrcoef( df[cols].values.T ) # df[cols].values.T : (n_instances, n_features) ==> (n_features, n_instances)
hm = heatmap(cm, row_names=cols, column_names=cols)

plt.show()

As you can see in the resulting figure, the correlation matrix provides us with another useful summary graphic that can help us to select features based on their respective linear correlations

To fit a linear regression model, we are interested in those features that have a high correlation with our target variable, MEDV. Looking at the previous correlation matrix, we can see that our target variable, MEDV, shows the largest correlation with the LSTAT variable (-0.74); however, as you might remember from inspecting the scatterplot matrix, there is a clear nonlinear relationship between LSTAT and MEDV. On the other hand, the correlation between RM and MEDV is also relatively high (0.70). Given the linear relationship between these two variables that we observed in the scatterplot, RM seems to be a good choice for an exploratory variable to introduce the concepts of a simple linear regression model in the following section.

Implementing an ordinary least squares linear regression model

At the beginning, it was mentioned that linear regression can be understood as obtaining the best-fitting straight line through the examples of our training data. However, we have neither defined the term best-fitting nor have we discussed the different techniques of fitting such a model. In the following subsections, we will fill in the missing pieces of this puzzle using the ordinary least squares (OLS) method (sometimes also called linear least squares) to estimate the parameters of the linear regression line that minimizes the sum of the squared vertical distances (residuals or errors) to the training examples.

Solving regression for regression parameters with gradient descent

Consider our implementation of the Adaptive Linear Neuron (Adaline) from cp02_TrainingSimpleMachineLearningAlgorithmsForClassification_meshgrid_ravel_contourf_OvA_GradientDecent https://blog.csdn.net/Linli522362242/article/details/96429442. You will remember that the artificial neuron uses a linear activation function. Also, we defined a cost function, J(w), which we minimized to learn the weights() via optimization algorithms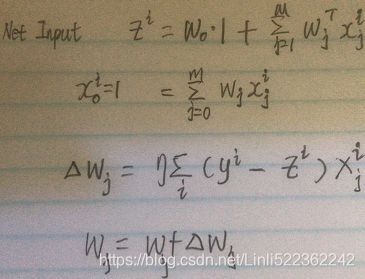, such as gradient descent (GD) and stochastic gradient descent (SGD, the step size is determined by the value of the learning rate). This cost function in Adaline is the sum of squared errors (SSE), which is identical to the cost function that we use for OLS:

Here, ̂ is the predicted value ̂ = (note that the term is just used for convenience to derive the update rule of GD). Essentially, OLS regression can be understood as Adaline without the unit step function so that we obtain continuous target values instead of the class labels -1 and 1. To demonstrate this, let's take the GD implementation of Adaline from cp02_TrainingSimpleMachineLearningAlgorithmsForClassification_meshgrid_ravel_contourf_OvA_GradientDecent https://blog.csdn.net/Linli522362242/article/details/96429442, and remove the unit step function to implement our first linear regression model:

class LinearRegressionGD(object):
    def __init__(self, eta=0.001, n_iter=20):
        self.eta = eta
        self.n_iter = n_iter
        
    def net_input(self, X):
        return np.dot(X, self.w_[1:]) + self.w_[0] # result's shape: (num_instances in X) ==(X.shape[0])
    
    def fit(self, X,y):
        self.w_ = np.zeros(1+X.shape[1]) # X.shape[1] : num_features
        # OR
        # rgen = np.random.RandomState(self.random_state)   #1+ num_features
        # self.w_ = rgen.normal( loc=0.0, scale=0.01, size=1+X.shape[1] )
        self.cost_ = []
        
        for i in range( self.n_iter ):
            output = self.net_input(X) # single column matrix
            errors = (y-output)
            self.w_[1:] += self.eta * X.T.dot(errors) # X.T : (num_features, num_instances)
            self.w_[0] += self.eta * errors.sum()
            cost = (errors**2).sum() /2.0
            self.cost_.append(cost)
        return self
    
    def predict(self,X):
        return self.net_input(X)

Weight updates with gradient descent

If you need a refresher about how the weights are updated—taking a step in the opposite direction of the gradient—please revisit the Adaptive linear neurons and the convergence of learning section in Chapter 2, Training Simple Machine Learning Algorithms for Classification.

To see our LinearRegressionGD regressor in action, let's use the RM (number of rooms) variable from the Housing dataset as the explanatory variable and train a model that can predict MEDV (house prices). Furthermore, we will standardize the variables for better convergence of the GD algorithm. The code is as follows:

X = df[['RM']].values # 2D array : 506 rows × 1 columns
y = df['MEDV'].values # 1D array

from sklearn.preprocessing import StandardScaler

sc_x = StandardScaler()
sc_y = StandardScaler()

X_std = sc_x.fit_transform(X)
y_std = sc_y.fit_transform(y[:, np.newaxis]).flatten() # y[:, np.newaxis] since fit_transform will take 2D array
                                                       # flatten() to 1D again
lr = LinearRegressionGD()
lr.fit(X_std, y_std)

Notice the workaround regarding y_std, using np.newaxis and flatten. Most transformers in scikit-learn expect data to be stored in two-dimensional arrays. In the previous code example, the use of np.newaxis in y[:, np.newaxis] added a new dimension to the array. Then, after StandardScaler returned the scaled variable, we converted it back to the original one-dimensional array representation using the flatten() method for our convenience.

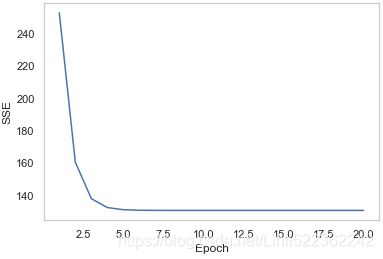
We discussed in Chapter 2, Training Simple Machine Learning Algorithms for Classification https://blog.csdn.net/Linli522362242/article/details/96429442, that it is always a good idea to plot the cost as a function of the number of epochs (complete iterations) over the training dataset when we are using optimization algorithms, such as GD, to check that the algorithm converged to a cost minimum (here, a global cost minimum):

plt.plot( range(1, lr.n_iter+1), 
          lr.cost_ )

plt.ylabel('SSE')
plt.xlabel('Epoch')
plt.grid(False)
plt.show()

As you can see in the following plot, the GD algorithm converged after the fifth epoch:

Next, let's visualize how well the linear regression line fits the training data. To do so, we will define a simple helper function that will plot a scatterplot of the training examples and add the regression line:

def lin_regplot(X,y, model):
    plt.scatter( X,y, c='steelblue', edgecolor='white', s=70 )
    plt.plot(X, model.predict(X), color='black', lw=2 )
    return # or # return None

Now, we will use this lin_regplot function to plot the number of rooms against the house price:

lin_regplot(X_std, y_std, lr)
plt.xlabel('Average number of rooms [RM] (standardized)' )
plt.ylabel('Price in $1000s [MEDV] (standardized)')

plt.show()

As you can see in the following plot, the linear regression line reflects the general trend that house prices tend to increase with the number of rooms:

Although this observation makes sense, the data also tells us that the number of rooms does not explain house prices very well in many cases. Later, we will discuss how to quantify量化 the performance of a regression model. Interestingly, we can also observe that several data points lined up at y = 3, which suggests that the prices may have been clipped(这意味着房价被限定了上界). In certain applications, it may also be important to report the predicted outcome variables on their original scale. To scale the predicted price outcome back onto the Price in $1000s axis, we can simply apply the inverse_transform method of the StandardScaler:

num_rooms_std = sc_x.transform( np.array([[5.0]]) )
price_std = lr.predict( num_rooms_std )
print('Price in $1000s: %.3f' % sc_y.inverse_transform(price_std) )

In this code example, we used the previously trained linear regression model to predict the price of a house with five rooms. According to our model, such a house will be worth $10,840.

As a side note, it is also worth mentioning that we technically don't have to update the weights of the intercept if we are working with standardized variables, since the y axis intercept is always 0 in those cases. We can quickly confirm this by printing the weights:

print('Slope: %.3f' % lr.w_[1])
print('Intercept: %.3f' % lr.w_[0])

Estimating the coefficient of a regression model via scikit-learn

In the previous section, we implemented a working model for regression analysis; however, in a real-world application, we may be interested in more efficient implementations. For example, many of scikit-learn's estimators for regression make use of the least squares implementation in SciPy (scipy.linalg.lstsq), which in turn uses highly optimized code optimizations based on the Linear Algebra Package (LAPACK). The linear regression implementation in scikit-learn also works (better) with unstandardized variables, since it does not use (S)GD-based optimization, so we can skip the standardization step:

from sklearn.linear_model import LinearRegression

slr = LinearRegression()
slr.fit(X,y)
y_pred = slr.predict(X)
print('Slope: %.3f' % slr.coef_[0])
print('Intercept: %.3f' % slr.intercept_)

As you can see from executing this code, scikit-learn's LinearRegression model, fitted with the unstandardized RM and MEDV variables, yielded different model coefficients, since the features have not been standardized. However, when we compare it to our GD implementation by plotting MEDV against RM, we can qualitatively see that it fits the data similarly well:

lin_regplot(X,y,slr)
plt.xlabel('Average number of rooms [RM]')
plt.ylabel('Price in %1000s [MEDV]')

plt.grid(False)
plt.show()

For instance, we can see that the overall result looks identical to our GD implementation:

Analytical solutions of linear regression

As an alternative to using machine learning libraries, there is also a closed-form solution for solving OLS involving a system of linear equations that can be found in most introductory statistics textbooks:

OR https://blog.csdn.net/Linli522362242/article/details/104005906

04_TrainingModels_Normal Equation(正态方程,正规方程) Derivation_Gradient Descent_Polynomial Regressionhttps://blog.csdn.net/Linli522362242/article/details/104005906

Equation 4-3. MSE cost function for a Linear Regression model

solve Normal Equation( has a closed-form solution) ==> find the value of θ (Minimum ==0 )==> minimizes MSE cost function ==> minimizes the RMSE

We can implement it in Python as follows:

# adding a column vector of "ones"

Xb = np.hstack(( np.ones( (X.shape[0], 1) ), X ))
w = np.zeros(X.shape[1])
z = np.linalg.inv( np.dot(Xb.T, Xb) )
w = np.dot(z, np.dot(Xb.T, y))

print('Slope: %.3f' % w[1])
print('Intercept: %.3f' % w[0])

The advantage of this method is that it is guaranteed to find the optimal solution analytically. However, if we are working with very large datasets, it can be computationally too expensive to invert the matrix in this formula (sometimes also called the normal equation), or the matrix containing the training examples may be singular (non-invertible), which is why we may prefer iterative methods in certain cases.

If you are interested in more information on how to obtain normal equations, take a look at Dr. Stephen Pollock's chapter The Classical Linear Regression Model from his lectures
at the University of Leicester, which is available for free at:http://www.le.ac.uk/users/dsgp1/COURSES/MESOMET/ECMETXT/06mesmet.pdf.

Also, if you want to compare linear regression solutions obtained via GD, SGD, the closed-form solution, QR factorization, and singular vector decomposition, you can use the LinearRegression class implemented in MLxtend (http://rasbt.github.io/mlxtend/user_guide/regressor/LinearRegression/), which lets users toggle between these options. Another great library to recommend for regression modeling in Python is Statsmodels, which implements more advanced linear regression models, as illustrated at https://www.statsmodels.org/stable/examples/index.html#regression.

Fitting a robust regression model using RANSAC

Linear regression models can be heavily impacted by the presence of outliers. In certain situations, a very small subset of our data can have a big effect on the estimated model coefficients. There are many statistical tests that can be used to detect outliers, which are beyond the scope of the book. However, removing outliers always requires our own judgment as data scientists as well as our domain knowledge.

As an alternative to throwing out outliers, we will look at a robust method of regression using the RANdom SAmple Consensus[kənˈsensəs]一致 (RANSAC) algorithm, which fits a regression model to a subset of the data, the so-called inliers.

We can summarize the iterative RANSAC algorithm as follows:

1. Select a random number of examples to be inliers and fit the model.
2. Test all other data points against the fitted model and add those points that fall within a user-given tolerance to the inliers.
3. Refit the model using all inliers.
4. Estimate the error of the fitted model versus the inliers.
5. Terminate the algorithm if the performance meets a certain user-defined threshold or if a fixed number of iterations were reached; go back to step 1 otherwise.

Let's now use a linear model in combination with the RANSAC algorithm as implemented in scikit-learn's RANSACRegressor class:

###############################################################

`sklearn.linear_model`.RANSACRegressor

class sklearn.linear_model.RANSACRegressor(base_estimator=None, *, min_samples=None, residual_threshold=None, is_data_valid=None, is_model_valid=None, max_trials=100, 
max_skips=inf, stop_n_inliers=inf, stop_score=inf, stop_probability=0.99, loss='absolute_loss', random_state=None

RANSAC (RANdom SAmple Consensus) algorithm.

RANSAC is an iterative algorithm for the robust estimation of parameters from a subset of inliers from the complete data set.

min_samples : int (>= 1) or float ([0, 1]), optional
Minimum number of samples chosen randomly from original data. Treated as an absolute number of samples for min_samples >= 1, treated as a relative number ceil(min_samples * X.shape[0]) for min_samples < 1. This is typically chosen as the minimal number of samples necessary to estimate the given base_estimator. By default a sklearn.linear_model.LinearRegression() estimator is assumed and min_samples is chosen as X.shape[1] + 1.

residual_threshold : float, optional
Maximum residual for a data sample to be classified as an inlier. By default the threshold is chosen as the MAD (median absolute deviation) of the target values y.

max_trials : int, optional
Maximum number of iterations for random sample selection.

loss : string, callable, optional, default “absolute_loss”
  String inputs, “absolute_loss” and “squared_loss” are supported which find the absolute loss and squared loss per sample respectively.
  If loss is a callable, then it should be a function that takes two arrays as inputs, the true and predicted value and returns a 1-D array with the i-th value of the array corresponding to the loss on X[i].
  If the loss on a sample is greater than the residual_threshold, then this sample is classified as an outlier.

Attributes:

inlier_mask_ : bool array of shape [n_samples]
Boolean mask of inliers classified as True.

###############################################################
04_TrainingModels_Normal Equation(正态方程,正规方程) Derivation_Gradient Descent_Polynomial Regression : https://blog.csdn.net/Linli522362242/article/details/104005906

from sklearn.linear_model import RANSACRegressor

ransac = RANSACRegressor( LinearRegression(),
                          max_trials = 100,
                          min_samples = 50,
                          loss = 'absolute_loss',
                          residual_threshold=5.0,
                          random_state=0 )
ransac.fit(X,y)

We set the maximum number of iterations of the RANSACRegressor to 100, and using min_samples=50, we set the minimum number of the randomly chosen training examples to be at least 50. Using 'absolute_loss' as an argument for the loss parameter, the algorithm computes absolute vertical distances between the fitted line and the training examples. By setting the residual_threshold parameter to 5.0, we only allow training examples to be included in the inlier set if their vertical distance to the fitted line(model) is within 5 distance units, which works well on this particular dataset. By default, scikit-learn uses the MAD estimate to select the inlier threshold, where MAD stands for the median absolute deviation of the target values, y. However, the choice of an appropriate value for the inlier threshold is problem-specific, which is one disadvantage of RANSAC. Many different approaches have been developed in recent years to select a good inlier threshold automatically. You can find a detailed discussion in Automatic Estimation of the Inlier Threshold in Robust Multiple Structures Fitting, R. Toldo, A. Fusiello's, Springer, 2009 (in Image Analysis and Processing–ICIAP 2009, pages: 123-131).

Once we have fitted the RANSAC model, let's obtain the inliers and outliers from the fitted RANSAC-linear regression model and plot them together with the linear fit:

inlier_mask = ransac.inlier_mask_
outlier_mask = np.logical_not( inlier_mask )

line_X = np.arange(3,10,1) # since the previous plot############################
line_y_ransac = ransac.predict( line_X[:, np.newaxis] )

plt.scatter( X[inlier_mask], y[inlier_mask],
             c='steelblue', edgecolor = 'white',
             marker='o', label='Inliers')
plt.scatter( X[outlier_mask], y[outlier_mask],
             c='limegreen', edgecolor='white',
             marker='s', label='Outliers')
plt.plot(line_X, line_y_ransac, color='black', lw=2)
plt.xlabel('Average number of rooms[RM]')
plt.ylabel('Price in $1000s [MEDV]')
plt.legend(loc='upper left')

plt.show()

As you can see in the following scatterplot, the linear regression model was fitted on the detected set of inliers, which are shown as circles:

When we print the slope and intercept of the model by executing the following code, the linear regression line will be slightly different from the fit that we obtained in the previous section without using RANSAC:

print('Slope: %.3f' % ransac.estimator_.coef_[0])
print('Intercept: %.3f' % ransac.estimator_.intercept_)

Using RANSAC, we reduced the potential effect of the outliers in this dataset, but we don't know whether this approach will have a positive effect on the predictive performance for unseen data or not. Thus, in the next section, we will look at different approaches for evaluating a regression model, which is a crucial part of building systems for predictive modeling.

Evaluating the performance of linear regression models

In the previous section, you learned how to fit a regression model on training data. However, you discovered in previous chapters that it is crucial to test the model on data that it hasn't seen during training to obtain a more unbiased estimate of its generalization performance.

As you will remember from cp6_Model Eval_Confusion_Hyperpara Tuning_pipeline_variance_bias_ validation_learning curve_strength https://blog.csdn.net/Linli522362242/article/details/109560084, we want to split our dataset into separate training and test datasets, where we will use the former to fit the model and the latter to evaluate its performance on unseen data to estimate the generalization performance. Instead of proceeding with the simple regression model, we will now use all variables in the dataset and train a multiple regression model:

from sklearn.model_selection import train_test_split

X = df.iloc[:, :-1].values #exclude the last feature(or the last column)
y = df['MEDV'].values

X_train, X_test, y_train, y_test = train_test_split(
    X, y, test_size=0.3, random_state=0
)

slr = LinearRegression()
slr.fit(X_train, y_train)
y_train_pred = slr.predict(X_train)
y_test_pred = slr.predict(X_test)

Since our model uses multiple explanatory variables, we can't visualize the linear regression line (or hyperplane, to be precise) in a two-dimensional plot, but we can plot the residuals (the differences or vertical distances between the actual and predicted values) versus the predicted values to diagnose our regression model. Residual plots are a commonly used graphical tool for diagnosing regression models. They can help to detect nonlinearity and outliers, and check whether the errors are randomly distributed.

Using the following code, we will now plot a residual plot where we simply subtract the true target variables from our predicted responses:

plt.figure(figsize=(10,8))
                           # residuals
plt.scatter( y_train_pred, y_train_pred - y_train,
             c='steelblue', marker='o', edgecolors='white',
             label = 'Training data' )
plt.scatter( y_test_pred, y_test_pred - y_test,
             c='limegreen', marker='s', edgecolors='white',
             label = 'Test data' )
plt.xlabel('Predicted values')
plt.ylabel('Residuals')
plt.legend( loc='upper left')
plt.hlines(y=0, xmin=-10, xmax=50, color='black', lw=2)
plt.xlim([-10,50])
plt.tight_layout()

plt.show()

After executing the code, we should see a residual plot with a line passing through the x axis origin, as shown here: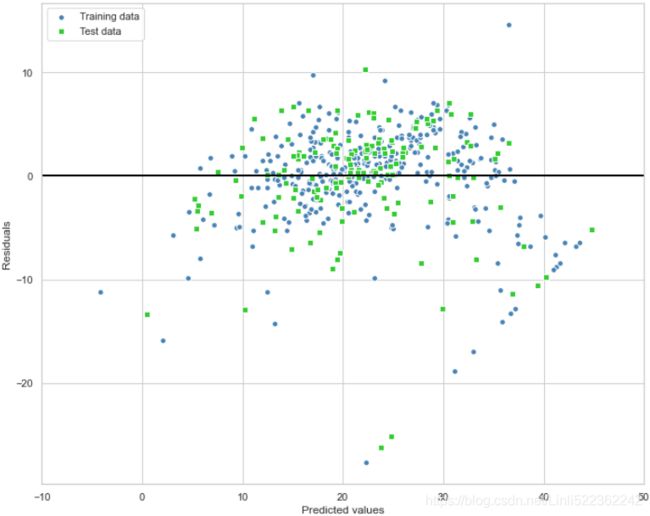

In the case of a perfect prediction, the residuals would be exactly zero, which we will probably never encounter in realistic and practical applications. However, for a good regression model, we would expect the errors to be randomly distributed and the residuals to be randomly scattered around the centerline. If we see patterns in a residual plot, it means that our model is unable to capture some explanatory information, which has leaked into the residuals, as you can slightly see in our previous residual plot. Furthermore, we can also use residual plots to detect outliers, which are represented by the points with a large deviation from the centerline.

Another useful quantitative measure of a model's performance is the so-called mean squared error (MSE), which is simply the averaged value of the SSE cost that we minimized to fit the linear regression model. The MSE is useful for comparing different regression models or for tuning their parameters via grid search and crossvalidation, as it normalizes the SSE by the sample size: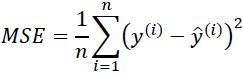

Let's compute the MSE of our training and test predictions:

from sklearn.metrics import mean_squared_error

print('MSE train: %.3f, test: %.3f' % ( mean_squared_error(y_train, y_train_pred),
                                        mean_squared_error(y_test, y_test_pred)
                                      ) )

You can see that the MSE on the training dataset is 19.96, and the MSE on the test dataset is much larger, with a value of 27.20, which is an indicator that our model is overfitting the training data in this case. However, please be aware that the MSE is unbounded in contrast to the classification accuracy, for example. In other words, the interpretation of the MSE depends on the dataset and feature scaling. For example, if the house prices were presented as multiples of 1,000 (with the K suffix), the same model would yield a lower MSE compared to a model that worked with unscaled features. To further illustrate this point, ($10K − 15K)^2 < ($10,000 − $15,000)^2 .

Thus, it may sometimes be more useful to report the coefficient of determination决定系数 () , which can be understood as a standardized version of the MSE, for better interpretability of the model's performance. Or, in other words, is the fraction of response variance响应方差的分数 that is captured by the model. The value is defined as:
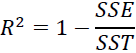OR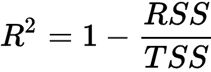
Here, SSE is the sum of squared errors(OR the sum of squared of residuals)
and SST is the total sum of squares: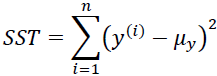

In other words, SST is simply the variance of the response.

Let's quickly show that is indeed just a rescaled version of the MSE: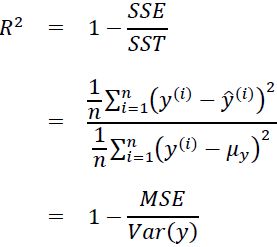
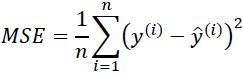# # rescaled y :

For the training dataset, the is bounded between 0 and 1, but it can become negative for the test dataset. If = 1 , the model fits the data perfectly with a corresponding MSE = 0(since Var(y)>0).

Evaluated on the training data, the of our model is 0.765, which doesn't sound too bad. However, the on the test dataset is only 0.673, which we can compute by executing the following code:

from sklearn.metrics import r2_score

print('R^2 train: %.3f, test: %.3f' % ( r2_score(y_train, y_train_pred),
                                        r2_score(y_test, y_test_pred)
                                      ) )

Coefficient of determination, in statistics, (or r^2), a measure that assesses the ability of a model to predict or explain an outcome in the linear regression setting. More specifically, R2 indicates the proportion of the variance方差 in the dependent variable 因变量(Y) that is predicted or explained by linear regression and the predictor variable (X, also known as the independent variable自变量).

The coefficient of determination shows only association. As with linear regression, it is impossible to use to determine whether one variable causes the other. In addition, the coefficient of determination shows only the magnitude of the association, not whether that association is statistically significant.

In general, a high R2 value indicates that the model is a good fit for the data, although interpretations of fit depend on the context of analysis. An R2 of 0.35, for example, indicates that 35 percent of the variation变动,差异 in the outcome has been explained just by predicting the outcome using the covariates(协变量, ) included in the model表明仅通过使用模型中包含的协变量, 预测结果即可解释结果差异的35％. That percentage might be a very high portion of variation to predict in a field such as the social sciences; in other fields, such as the physical sciences, one would expect R2 to be much closer to 100 percent. The theoretical minimum R2 is 0. However, since linear regression is based on the best possible fit, R2 will always be greater than zero, even when the predictor(X) and outcome variables(Y) bear no relationship to one another.
OR

R2 increases when a new predictor variable is added to the model, even if the new predictor is not associated with the outcome. To account for that effect, the adjusted R2 (typically denoted with a bar over the R in R2) incorporates the same information as the usual but then also penalizes for the number(k) of predictor variables included in the model. As a result, R2 increases as new predictors are added to a multiple linear regression model, but the adjusted R2 increases only if the increase in R2 is greater than one would expect from chance alone仅当新项对模型的改进超出偶然的预期时，the adjusted R2 才会增加. It decreases when a predictor improves the model by less than expected by chance.In such a model, the adjusted R2 is the most realistic estimate of the proportion of the variation that is predicted by the covariates included in the model

Using regularized methods for regression

As we discussed in cp3 A Tour of ML Classifiers_stratify_bincount_likelihood_logistic regression_odds ratio_decay_L2 https://blog.csdn.net/Linli522362242/article/details/96480059, regularization(e.g. L2 shrinkage or weight decay) is one approach to tackling the problem of overfitting by adding additional information, and thereby shrinking the parameter values of the model to induce a penalty against complexity. The most popular approaches to regularized linear regression are the so-called Ridge Regression, least absolute shrinkage and selection operator (LASSO), and elastic Net.

Ridge Regression is an L2 penalized model where we simply add the squared sum of the weights to our least-squares cost function :https://blog.csdn.net/Linli522362242/article/details/104070847 and https://blog.csdn.net/Linli522362242/article/details/108230328
minus Predicted_y :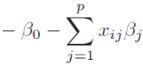
OR OR
Here:
#######################################################################################

Note(is different with MSE(Mean Square of Error) since ）: is different with MSE(Mean Square of Error) since ）:

#######################################################################################

By increasing the value of hyperparameter , we increase the regularization strength and thereby shrink the weights of our model. Please note that we don't regularize the intercept term, .
##################################Here ==W

将 (3.41) 的准则写成矩阵形式
可以简单地看出岭回归的解为（本质在自变量信息矩阵的主对角线元素上人为地加入一个非负因子）

##################################

An alternative approach that can lead to sparse models is LASSO. Depending on the regularization strength, certain weights can become zero, which also makes LASSO useful as a supervised feature selection technique: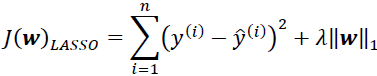
OR
Here, the L1 penalty for LASSO is defined as the sum of the absolute magnitudes of the model weights, as follows:

However, a limitation of LASSO is that it selects at most n features if m > n, where n is the number of training examples. This may be undesirable in certain applications of feature selection. In practice, however, this property of LASSO is often an advantage because it avoids saturated models. Saturation of a model occurs if the number of training examples is equal to the number of features, which is a form of overparameterization过度参数化. As a consequence, a saturated model can always fit the training data perfectly but is merely a form of interpolation插补 and thus is not expected to generalize well.

A compromise between Ridge Regression and LASSO is elastic net, which has an L1 penalty to generate sparsity(Lasso Regression automatically performs feature selection and outputs a sparse model (i.e., with few nonzero feature weights).) and an L2 penalty such that it can be used for selecting more than n features if m > n:

######################################################https://blog.csdn.net/Linli522362242/article/details/104070847

If α = 0 then Ridge Regression is just Linear Regression.
If α(inverse of ) is very large, then all weights end up very close to zero and the result is a flat line going through the data’s mean

Note how increasing α leads to flatter (i.e., less extreme, more reasonable) predictions; this reduces the model’s variance but increases its bias.
https://blog.csdn.net/Linli522362242/article/details/108230328
in the preceding figure, we can see that the contour of the cost function touches the L1 diamond at . Since the contours of an L1 regularized system are sharp, it is more likely that the optimum—that is, the intersection between the ellipses of the cost function and the boundary of the L1 diamond—is located on the axes, which encourages sparsity. The mathematical details of why L1 regularization can lead to sparse solutions are beyond the scope of this book. If you are interested, an excellent section on L2 versus L1 regularization can be found in section 3.4 of The Elements of Statistical Learning, Trevor Hastie, Robert Tibshirani, and Jerome Friedman, Springer.

by increasing the regularization strength via the regularization parameter , we shrink the weights towards zero and decrease the dependence of our model on the training data. Let's illustrate this concept in the following figure for the L2 penalty term.

The quadratic L2 regularization term is represented by the shaded ball. Here, our weight coefficients cannot exceed our regularization budget—the combination of the weight coefficients###W=w1, w2, w3...wn### cannot fall outside the shaded area. On the other hand, we still want to minimize the cost function(such as The term is just added for our convenience https://blog.csdn.net/Linli522362242/article/details/96480059). Under the penalty constraint, our best effort is to choose the point where the L2 ball intersects with the contours of the unpenalized cost function. The larger the value of the regularization parameter gets, the faster the penalized cost functiongrows, which leads to a narrower L2 ball. For example, if we increase the regularization parameter towards infinity, the weight coefficients will become effectively zero, denoted by the center of the L2 ball. To summarize the main message of the example: our goal is to minimize the sum of the unpenalized cost function plus the penalty term, which can be understood as adding bias and preferring a simpler model to reduce the variance(try to underfit) in the absence of sufficient training data to fit the model.
######################################################

Those regularized regression models are all available via scikit-learn, and their usage is similar to the regular regression model except that we have to specify the regularization strength via the parameter , for example, optimized via k-fold crossvalidation.

A Ridge Regression model can be initialized via:

from sklearn.linear_model import Ridge

ridge = Ridge(alpha=1.0)

#################################################

As with Linear Regression, we can perform Ridge Regression either by computing a closed-form equation or by performing Gradient Descent. The pros and cons are the same. Equation 4-9 shows the closed-form solution (where A is the n × n identity单位 matrix A( A square matrix full of 0s except for 1s on the main diagonal (top-left to bottom-right). ) except with a 0 in the top-left cell, corresponding to the bias term ).

Equation 4-9. Ridge Regression closed-form solution

Note: Normal Equation(a closed-form equation)
Here is how to perform Ridge Regression with Scikit-Learn using a closed-form solution (a variant of Equation 4-9 using a matrix factorization technique by André-Louis Cholesky):

from sklearn.linear_model import Ridge
ridge_reg = Ridge(alpha=1, solver="cholesky", random_state=42)
ridge_reg.fit(X,y)  
ridge_reg.predict([[1.5]])

ridge_reg = Ridge(alpha=1, solver="sag", random_state=42)
ridge_reg.fit(X,y)
ridge_reg.predict([[1.5]])

solver{‘auto’, ‘svd’, ‘cholesky’, ‘lsqr’, ‘sparse_cg’, ‘sag’, ‘saga’}, default=’auto’

Solver to use in the computational routines:

‘auto’ chooses the solver automatically based on the type of data.
‘svd’ uses a Singular Value Decomposition(https://blog.csdn.net/Linli522362242/article/details/105139547) of X to compute the Ridge coefficients. More stable for singular matrices than ‘cholesky’.
‘cholesky’ uses the standard scipy.linalg.solve function to obtain a closed-form solution.
‘sparse_cg’ uses the conjugate gradient solver共轭梯度求解器 as found in scipy.sparse.linalg.cg. As an iterative algorithm, this solver is more appropriate than ‘cholesky’ for large-scale data (possibility to set tol and max_iter).
‘lsqr’ uses the dedicated regularized least-squares routine scipy.sparse.linalg.lsqr. It is the fastest and uses an iterative procedure.
‘sag’ uses a Stochastic Average Gradient descent, and ‘saga’ uses its improved, unbiased version named SAGA. Both methods also use an iterative procedure, and are often faster than other solvers when both n_samples and n_features are large. Note that ‘sag’ and ‘saga’ fast convergence is only guaranteed on features with approximately the same scale. You can preprocess the data with a scaler from sklearn.preprocessing.

#################################################

Note that the regularization strength is regulated by the parameter alpha, which is similar to the parameter . Likewise, we can initialize a LASSO regressor from the linear_model submodule:

from sklearn.linear_model import Lasso

lasso = Lasso(alpha=1.0)

Lastly, the ElasticNet implementation allows us to vary the L1 to L2 ratio:
OR https://blog.csdn.net/Linli522362242/article/details/104070847

from sklearn.linear_model import ElasticNet

elasticNet = ElasticNet( alpha=1.0, l1_ratio=0.5)

For example, if we set the l1_ratio to 1.0, the ElasticNet regressor would be equal to LASSO regression. For more detailed information about the
different implementations of linear regression, please see the documentation at http://scikit-learn.org/stable/modules/linear_model.html.

Turning a linear regression model into a curve – polynomial regression

In the previous sections, we assumed a linear relationship between explanatory and response variables. One way to account for the violation of linearity assumption is to use a polynomial regression model by adding polynomial terms:

Here, d denotes the degree of the polynomial. Although we can use polynomial regression to model a nonlinear relationship, it is still considered a multiple linear regression model because of the linear regression coefficients, w. In the following subsections, we will see how we can add such polynomial terms to an existing dataset conveniently and fit a polynomial regression model.

Adding polynomial terms using scikit-learn

We will now learn how to use the PolynomialFeatures transformer class from scikit-learn to add a quadratic term (d = 2) to a simple regression problem with one
explanatory variable. Then, we will compare the polynomial to the linear fit by following these steps:
1. Add a second-degree polynomial term:

X = np.array([258.0, 270.0, 294.0, 
              320.0, 342.0, 368.0, 
              396.0, 446.0, 480.0, 586.0])\
             [:, np.newaxis]

y = np.array([236.4, 234.4, 252.8, 
              298.6, 314.2, 342.2, 
              360.8, 368.0, 391.2,
              390.8])

from sklearn.preprocessing import PolynomialFeatures

X_new = np.arange(250, 600, 10)[:, np.newaxis] # array([ [250],[260],..., [590] ])

# 2. Fit a simple linear regression model for comparison:
lr = LinearRegression()
lr.fit(X,y)
y_lin_fit = lr.predict(X_new)

# 4. fit quadratic features
pr = LinearRegression()
# So let’s use Scikit-Learn’s PolynomialFeatures class to transform our training data, 
# adding the square (2nd-degree polynomial) of each feature in the training set as new features 
# (in this case there is just one feature):
quadratic = PolynomialFeatures(degree=2)
X_quad = quadratic.fit_transform(X)
#          bias=1           258.0   66,564
# X_quad
# array([[1.00000e+00, 2.58000e+02, 6.65640e+04],
#        [1.00000e+00, 2.70000e+02, 7.29000e+04],
#        [1.00000e+00, 2.94000e+02, 8.64360e+04],
#        [1.00000e+00, 3.20000e+02, 1.02400e+05],
#        [1.00000e+00, 3.42000e+02, 1.16964e+05],
#        [1.00000e+00, 3.68000e+02, 1.35424e+05],
#        [1.00000e+00, 3.96000e+02, 1.56816e+05],
#        [1.00000e+00, 4.46000e+02, 1.98916e+05],
#        [1.00000e+00, 4.80000e+02, 2.30400e+05],
#        [1.00000e+00, 5.86000e+02, 3.43396e+05]])
pr.fit(X_quad, y)
y_quad_fit = pr.predict( quadratic.fit_transform(X_new) )

# 4. Plot the results:
plt.scatter( X,y,label='Traning points' )
plt.plot( X_new, y_lin_fit, label='Linear fit', linestyle='--' )
plt.plot( X_new, y_quad_fit, label='Quadratic fit')
plt.xlabel('Explanatory variable')
plt.ylabel('Predicted or known target values')
plt.legend( loc='upper left')

plt.tight_layout()
plt.show()

In the resulting plot, you can see that the polynomial fit captures the relationship between the response(Y) and explanatory variables(X) much better than the linear fit:

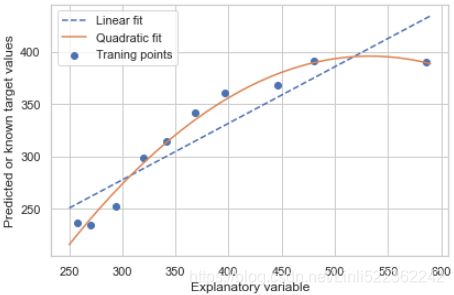
Next, we will compute the MSE and evaluation metrics:

y_lin_pred = lr.predict(X)
y_quad_pred = pr.predict(X_quad)

print( 'Training MSE linear: %.3f, quadratic: %.3f' % ( mean_squared_error(y, y_lin_pred),
                                                        mean_squared_error(y, y_quad_pred)
                                                      ) )
print( 'Train R^2 linear: %.3f, quadratic: %.3f' % ( r2_score(y, y_lin_pred),
                                                     r2_score(y, y_quad_pred) 
                                                   ) )

As you can see after executing the code, the MSE decreased from 570 (linear fit) to 61 (quadratic fit); also, the coefficient of determination决定系数 () reflects a closer fit of the quadratic model ( = 0.982 ) as opposed to the linear fit ( = 0.832 ) in this particular toy problem.a high R2 value indicates that the model is a good fit for the data

Modeling nonlinear relationships in the Housing dataset

In the preceding subsection, you learned how to construct polynomial features to fit nonlinear relationships in a toy玩物/简单 problem; let's now take a look at a more concrete example and apply those concepts to the data in the Housing dataset. By executing the following code, we will model the relationship between house prices and LSTAT (percentage of lower status of the population) using second-degree (quadratic) and third-degree (cubic) polynomials and compare that to a linear fit:

df.head()

###########################################################################

class sklearn.preprocessing.PolynomialFeatures(degree=2, *, interaction_only=False, include_bias=True, order='C')

Parameters

degree : int, default=2
The degree of the polynomial features.
interaction_only : bool, default=False
If true, only interaction features are produced: features that are products of at most degree distinct input features (so not x[1]**2, x[0]*x[2]**3, etc.).
include_bias : bool, default=True
If True (default), then include a bias column, the feature in which all polynomial powers are zero (i.e. a column of ones - acts as an intercept term in a linear model).
order : {‘C’, ‘F’}, default=’C’
Order of output array in the dense case. ‘F’ order is faster to compute, but may slow down subsequent estimators.

Consider the 2D array arr = np.arange(12).reshape(3,4). It looks like this:

In a computer memory this is stored as

This is also known as row-major order methods for storing multidimensional arrays in linear storage such as random access memory.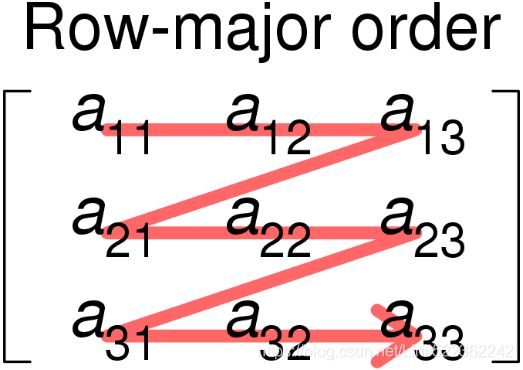
It is also called as C Contiguous layout (order ‘C’) because C arrays always start at zero and stored as contiguous block of memory. So the next memory address holds the next row value on that row.
For example, the array

The array A elements in C arrays are row major order as shown in this table https://en.wikipedia.org/wiki/Row-_and_column-major_order#/media/File:Row_and_column_major_order.svg

Fortran Contiguous or Column major

if you transpose the above array then it becomes Fortran contiguous layout i.e. order ‘F’
[ [a11, a21],
[a12, a22],
[a13, a23] ]
By default Fortran arrays start at 1 and also known as column-major order methods for storing multidimensional arrays in linear storage such as RAM

The array A elements in F contiguous arrays are column major order as shown in below table

The C contiguous memory layout, row-wise operations are usually faster than column-wise operations(A typical rowwise operation is to compute row means or row sums, for example to compute person sum scores for psychometric analyses.)

Similarly column wise operation is faster for F contiguous array

So we have understood what is conguous array and what is order difference between C and Fortran(F) and now we can explore numpy.ravel() and numpy.reshape()

numpy ravel explained

numpy.ravel(array, order=’C’)

order = {‘C’,’F’, ‘A’, ‘K’}, optional and by default it is ‘C’

‘A’ means to read the elements in Fortran-like index order if array is Fortran contiguous in memory, C-like order otherwise
and ‘K’ means to read the elements in the order they occur in memory

x = np.array([[1, 2, 3], [4, 5, 6]])
x

np.ravel(x)

<== default order='C'

np.ravel(x, order='F')

<==

numpy ravel with order A

x.T

np.ravel(x.T)

<==

np.ravel(x.T,order='A')

<==

numpy.reshape()

numpy.reshape(a, newshape, order=’C’)

order = {‘C’,’F’, ‘A’, ‘K’}, optional and by default it is ‘C’

x = np.array([[1, 2, 3], [4, 5, 6]])
x

This a 2x3 array and we want to reshape it to 3x2

np.reshape(x,(3,2))

np.reshape(np.ravel(x),(3,2))

<== np.ravel(x)<==

np.reshape(np.ravel(x),(3,-1))

The output is same here as previous one with shape (3,2) because when dimension -1 is given then it infers the value as 2 based on original shape of array

###########################################################################

X = df[['LSTAT']].values
y = df['MEDV'].values

regr = LinearRegression()

# create quadratic features
quadratic = PolynomialFeatures( degree=2 )
cubic = PolynomialFeatures( degree=3 )
X_quad = quadratic.fit_transform(X)
X_cubic = cubic.fit_transform(X)

# fit features
X_new = np.arange( X.min(), X.max(), 1 )[:, np.newaxis] # 1D==>2D

regr = regr.fit(X,y)
linear_r2 = r2_score(y, regr.predict(X))    # get the training r2 score
y_new_lin_fit = regr.predict(X_new)

regr = regr.fit(X_quad, y)
quadratic_r2 = r2_score(y, regr.predict(X_quad)) # get the training r2 score
y_new_quad_fit = regr.predict( quadratic.fit_transform(X_new) )

regr = regr.fit(X_cubic, y)
cubic_r2 = r2_score(y, regr.predict(X_cubic))     # get the training r2 score
y_new_cubic_fit = regr.predict( cubic.fit_transform(X_new) )

#plot results
plt.figure(figsize=(10,8))
plt.scatter( X,y, label='Traning points', color='lightgray')

plt.plot( X_new, y_new_lin_fit,
          label = 'Linear (d=1), $R^2=%.2f$' % linear_r2,
          color = 'blue',
          lw = 2,
          linestyle = ':' )

plt.plot( X_new, y_new_quad_fit,
          label = 'Quadratic (d=2), $R^2=%.2f$' % quadratic_r2,
          color = 'red',
          lw = 2,
          ls = '-' )

plt.plot( X_new, y_new_cubic_fit,
          label = 'Cubic (d=3), $R^2=%.2f$' % cubic_r2,
          color = 'green',
          lw = 2,
          ls = '--' )

plt.xlabel( '% lower status of the population [LSTAT]' )
plt.ylabel( 'Price in $1000s [MEDV]' )
plt.legend( loc='upper right' )

plt.show()

The resulting plot is as follows:

LSTAT : Percentage of lower status地位 of the population
##########################################################################
Why MEDV vs LSTAT since and the largest correlation with the LSTAT
variable (-0.74)
the correlation matrix(rescaled version of the covariance matrix, a correlation matrix to quantify量化 and summarize linear relationships between variables)
##########################################################################

As you can see, the cubic fit(with the highest R2 score) captures the relationship between house prices and LSTAT better than the linear and quadratic fit. However, you should be aware that adding more and more polynomial features increases the complexity of a model and therefore increases the chance of overfitting. Thus, in practice, it is always recommended to evaluate the performance of the model on a separate test dataset to estimate the generalization performance.

In addition, polynomial features are not always the best choice for modeling nonlinear relationships. For example, with some experience or intuition, just looking at the MEDV-LSTAT scatterplot may lead to the hypothesis that a log-transformation of the LSTAT feature variable and the square root of MEDV(Median value of owner-occupied homes in $1000s) may project the data onto a linear feature space suitable for a linear regression fit. For instance, my perception is that this relationship between the two variables looks quite similar to an exponential function:
Note (e^-1)^x and 0<(e^-1) <1
Since the natural logarithm of an exponential function is a straight line, I assume that such a log-transformation can be usefully applied here:

Let's test this hypothesis by executing the following code:

# transform features
X_log = np.log(X) # since the hypothesis: y=e^(-X), then log(e^-X)=-X ==> a straight line
y_sqrt = np.sqrt(y)

# fit features
X_new_log = np.arange( X_log.min()-1, X_log.max()+1, 1)[:, np.newaxis]

regr = regr.fit( X_log, y_sqrt )
linear_r2 = r2_score( y_sqrt, regr.predict(X_log) )
y_new_lin_fit = regr.predict( X_new_log )

# plot results
plt.scatter( X_log, y_sqrt, label='Training poits', color='lightgray' )

plt.plot( X_new_log, y_new_lin_fit,
          label = 'Linear (d=1), $R^2=%.2f$' % linear_r2,
          color = 'blue',
          lw=2 )

plt.xlabel( 'log(% lower status of the population [LSTAT])' )
plt.ylabel( '$\sqrt{Price \; in \; \$1000s \; [MEDV]}$' ) # OR # plt.ylabel( '$\sqrt{Price\;in\;\$1000s\;[MEDV]}$' )
plt.legend( loc='lower left' )

plt.tight_layout()
plt.show()

After transforming the explanatory onto the log space and taking the square root of the target variables, we were able to capture the relationship between the two variables with a linear regression line that seems to fit the data better (2 = 0.69 ) than any of the previous polynomial feature transformations: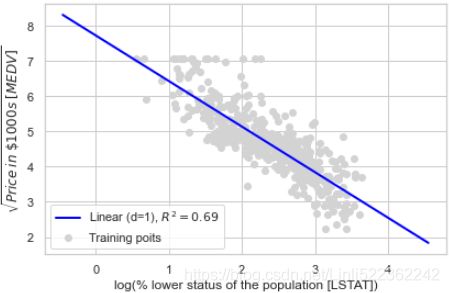

Dealing with nonlinear relationships using random forests

In this section, we are going to take a look at random forest regression, which is conceptually different from the previous regression models in this chapter. A random forest, which is an ensemble of multiple decision trees, can be understood as the sum of piecewise linear functions, in contrast to the global linear and polynomial regression models that we discussed previously. In other words, via the decision tree algorithm, we subdivide the input space into smaller regions that become more manageable.

Decision tree regression

An advantage of the decision tree algorithm is that it does not require any transformation of the features if we are dealing with nonlinear data, because decision trees analyze one feature at a time, rather than taking weighted combinations into account. (Likewise, normalizing or standardizing features is not required for decision trees.) You will remember from Cp3 ML Classifiers_2_support vector_Maximum margin_soft margin_C~slack_kernel_Gini_pydot+_Information Gain https://blog.csdn.net/Linli522362242/article/details/107755405, that we grow a decision tree by iteratively splitting its nodes until the leaves are pure or a stopping criterion is satisfied. When we used decision trees for classification, we defined entropy as a measure of impurity to determine which feature split maximizes the information gain (IG) , which can be defined as follows for a binary split: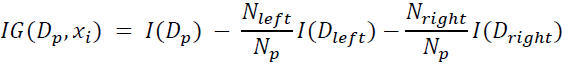
（信息增益=父节点data set的总不纯度（含有有用的信息）-权重*左节点data set的不纯度-权重*右节点的data set不纯度，每次分割都能获得信息增益）
Here, is the subset of training examples at the parent node, is the feature to perform the split, is the total number of samples at the parent node, I is the impurity function, , and and are the subsets of training examples at the left and right child nodes after the split. is the number of samples in the jth child node (Here j=left or right). Remember that our goal is to find the feature split that maximizes the information gain; in other words, we want to find the feature split that reduces the impurities in the child nodes most（找到特征划分使得的子节点中信息不纯度最低（或者最大减少子节点的不纯度））. In Cp3 ML Classifiers_2_support vector_Maximum margin_soft margin_C~slack_kernel_Gini_pydot+_Information Gain https://blog.csdn.net/Linli522362242/article/details/107755405, we discussed
Gini impurity (Gini index, as a measure of node purity—a small value indicates that a node contains predominantly显著地 observations(or samples) from a single class(c=1); 0 ≤ ≤ 1, OR 0 ≤ ˆpmk ≤ 1;

########################################06_Decision Trees_01_graphviz_Gini_Entropy_Decision Tree_CART_prune_Regression_Classification_Treehttps://blog.csdn.net/Linli522362242/article/details/104542381

To compute Gini impurity for a set of items with classes, suppose , and let be the fraction of items labeled with class in the set. （ is the proportion of class i in the set）

: the sum of all probabilities of all classes(J) is equal to 1.

example:
and 1 == + +
########################################https://blog.csdn.net/Linli522362242/article/details/104542381
eg, K=2, means the mth node is relatively pure, p=0.9, p *q= 0.9*0.1== 0.09, Gini index at mth node=0.9*0.1+0.1*0.9=0.18; the Gini impurity is maximal if the classes are perfectly mixed(distributed uniformly), for example, in a binary class setting ( ):

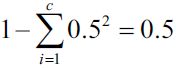
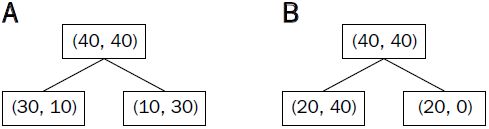
We start with a dataset at the parent node that consists of 40 samples from class 1 and 40 samples from class 2 that we split into two datasets and , respectively.

However, the Gini impurity would favor the split in scenario B( ) over scenario A(), which is indeed more pure: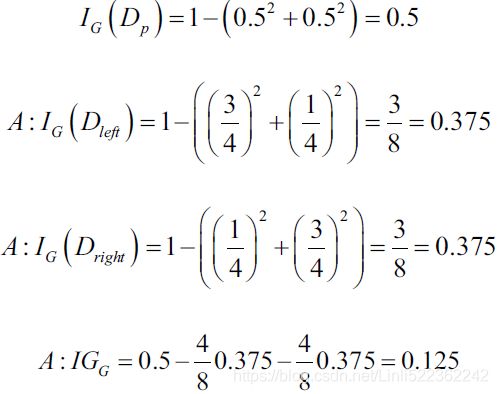

)
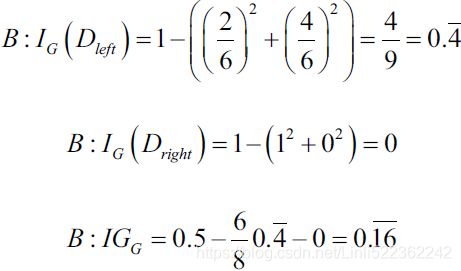
and entropy (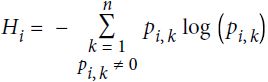OR 0 ≤ ≤ 1, Here, is the proportion of the samples that belongs to class i for a particular node t. The entropy is therefore 0 if all samples at a node belong to the same class, and the entropy is maximal if we have a uniform class distribution. For example, in a binary class setting, the entropy is 0(= -(1*0 + 0*(0)) ) if p (i =1| t ) =1 or p(i = 0 | t ) = 0. If the classes are distributed uniformly with p (i =1| t ) = 0.5 and p(i = 0 | t ) = 0.5, the entropy is 1(= - (0.5*-1 + 0.5*-1) ) . Therefore, we can say that the entropy criterion attempts to maximize the mutual information in the tree.
##########################################https://blog.csdn.net/Linli522362242/article/details/104542381

We start with a dataset at the parent node that consists of 40 samples from class 1 and 40 samples from class 2 that we split into two datasets and , respectively.

the entropy criterion would favor scenario B( ) over scenario () :

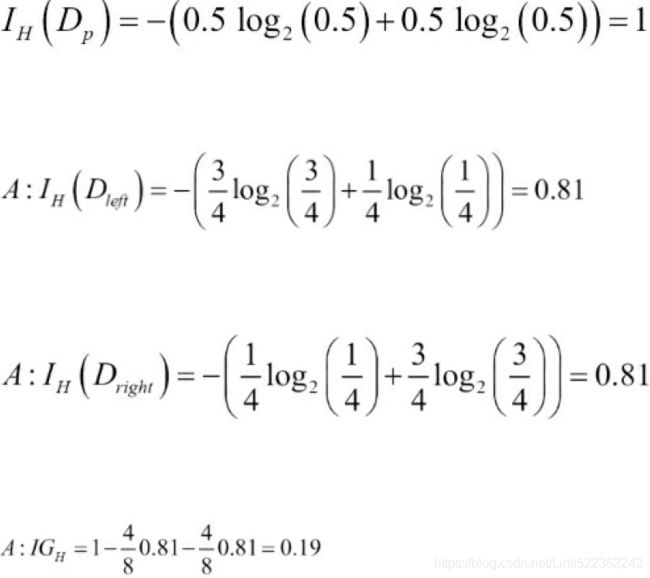
Gini impurity is slightly faster to compute, so it is a good default. However, when they differ, Gini impurity tends to isolate the most frequent class in its own branch of the tree, while entropy tends to produce slightly more balanced trees.

(more times of spliting a dataset, larger size to the tree, more number of leaf nodes(and each leaf may just contain fewer data points or samples) and the model become more complexity, but minimizes residual errors )

##########################################https://blog.csdn.net/Linli522362242/article/details/104542381

)
as measures of impurity, which are both useful criteria for classification. To use a decision tree for regression, however, we need an impurity metric that is suitable for continuous variables, so we define the impurity measure of a node, t, as the MSE instead:

Here, is the number of training samples at node t , is the training subset at node t , is the true target value, and is the predicted target value (sample mean):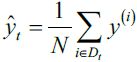

############################
The pruning is based on a criterion that balances residual error against a measure of model complexity. If we denote the starting tree for pruning by , then we define to be a subtree of if it can be obtained by pruning nodes from (in other words, by collapsing折叠 internal nodes by combining the corresponding regions即通过合并对应区域来收缩内部结点). Suppose the leaf nodes are indexed by τ = 1, . . . , |T|, with leaf node τ representing a region of input space having data points(samples), and |T| denoting the total number of leaf nodes. The optimal prediction for region is then given by 那么区域给出的最优的预测为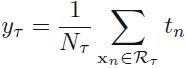

and the corresponding contribution to the residual sum-of-squares is then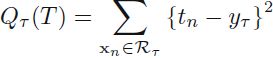
The pruning criterion is then given by (minimizing)

The regularization parameter λ determines the trade-off between the overall residual sum-of-squares error and the complexity of the model as measured by the number |T| of leaf nodes, and its value is chosen by cross-validation.

########################################################06_Decision Trees_01_graphviz_Gini_Entropy_Decision Tree_CART_prune_Regression_Classification_Treehttps://blog.csdn.net/Linli522362242/article/details/104542381

In the context of decision tree regression, the MSE is often also referred to as within-node variance, which is why the splitting criterion is also better known as variance reduction. To see what the line fit of a decision tree looks like, let's use the DecisionTreeRegressor implemented in scikit-learn to model the nonlinear relationship between the MEDV and LSTAT variables:

from sklearn.tree import DecisionTreeRegressor

X = df[['LSTAT']].values
y = df['MEDV'].values

tree = DecisionTreeRegressor( max_depth=3 )
tree.fit(X,y)

def lin_regplot(X,y, model):
    plt.scatter( X,y, c='steelblue', edgecolor='white', s=70 )
    plt.plot(X, model.predict(X), color='black', lw=2 )
    return # or # return None

sort_idx = X.flatten().argsort() # return index after sorting X.flatten()

lin_regplot(X[sort_idx], y[sort_idx], tree)
plt.xlabel('% lower status of the population [LSTAT]')
plt.ylabel('Price in $1000s [MEDV]')

plt.show()

As we can see from the resulting plot, the decision tree captures the general trend in the data. However, a limitation of this model is that it does not capture the continuity and differentiability of the desired prediction. In addition, we need to be careful about choosing an appropriate value for the depth of the tree to not overfit or underfit the data; here, a depth of 3 seems to be a good choice: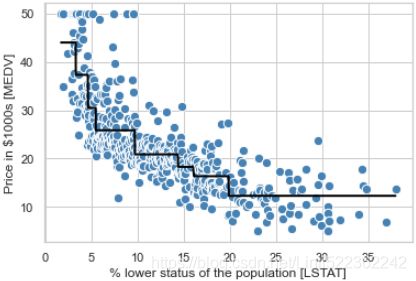
2^3=8
In the next section, we will take a look at a more robust way for fitting regression trees: random forests.
#########################################################

class sklearn.tree.DecisionTreeRegressor(*, criterion='mse', splitter='best', max_depth=None, min_samples_split=2, 
                                         min_samples_leaf=1, min_weight_fraction_leaf=0.0, max_features=None, 
                                         random_state=None, max_leaf_nodes=None, min_impurity_decrease=0.0, 
                                         min_impurity_split=None, ccp_alpha=0.0)

criterion : {“mse”, “friedman_mse”, “mae”, “poisson”}, default=”mse”

The function to measure the quality of a split. Supported criteria are “mse” for the mean squared error, which is equal to variance reduction as feature selection criterion and minimizes the L2 loss using the mean of each terminal node, “friedman_mse”, which uses mean squared error with Friedman’s improvement score for potential splits, “mae” for the mean absolute error, which minimizes the L1 loss using the median of each terminal node, and “poisson” which uses reduction in Poisson deviance to find splits.

max_depth : int, default=None

The maximum depth of the tree. If None, then nodes are expanded until all leaves are pure or until all leaves contain less than min_samples_split samples.

min_impurity_decrease : float, default=0.0

A node will be split if this split induces a decrease of the impurity greater than or equal to this value.

The weighted impurity decrease equation is the following:

N_t / N * (impurity - N_t_R / N_t * right_impurity
                    - N_t_L / N_t * left_impurity)

where N is the total number of samples,
N_t is the number of samples at the current node,
N_t_L is the number of samples in the left child, and
N_t_R is the number of samples in the right child.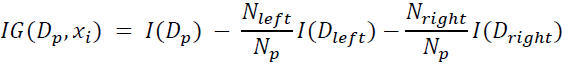

#########################################################

Random forest regression

As we discussed in cp3 A Tour of ML Classifiers_3_ random forests_knn https://blog.csdn.net/Linli522362242/article/details/107843678, the random forest algorithm is an ensemble technique that combines multiple decision trees. A random forest usually has a better generalization performance than an individual decision tree due to randomness that helps to decrease the model variance. Other advantages of random forests are that they are less sensitive to outliers in the dataset and don't require much parameter tuning. The only parameter in random forests that we typically need to experiment with is the number of trees in the ensemble. The basic random forests algorithm for regression is almost identical to the random forest algorithm for classification that
we discussed in Cp3. The only difference is that we use the MSE criterion to grow the individual decision trees, and the predicted target variable is calculated as the average prediction over all decision trees.

Now, let's use all the features in the Housing Dataset to fit a random forest regression model on 60 percent of the samples and evaluate its performance on the remaining 40 percent. The code is as follows:

from sklearn.ensemble import RandomForestRegressor

forest = RandomForestRegressor( n_estimators=1000,
                                criterion='mse',
                                random_state=1,
                                n_jobs=-1)
forest.fit(X_train, y_train)
y_train_pred = forest.predict(X_train)
y_test_pred = forest.predict(X_test)

print( 'MSE train: %.3f, test: %.3f' % ( mean_squared_error(y_train, y_train_pred),
                                         mean_squared_error(y_test, y_test_pred)
                                       ) )
print( 'R^2 train: %.3f, test: %.3f' % ( r2_score(y_train, y_train_pred),
                                         r2_score(y_test, y_test_pred) 
                                       ) )

Unfortunately, we see that the random forest tends to overfit the training data. However, it's still able to explain the relationship between the target and explanatory variables relatively well ( R2 = 0.871 on the test dataset).

Lastly, let's also take a look at the residuals of the prediction:

plt.scatter( y_train_pred,
             y_train_pred - y_train,
             c='steelblue',
             edgecolors='white',
             marker='o',
             s=35,
             alpha=0.9,
             label='Training data' )
plt.scatter( y_test_pred,
             y_test_pred - y_test,
             c='limegreen',
             edgecolors='white',
             marker='s',
             s=35,
             alpha=0.9,
             label='Test data')

plt.xlabel('Predicted values')
plt.ylabel('Residuals')
plt.legend(loc='upper left')
plt.hlines(y=0, xmin=-10, xmax=50, lw=2, color='black')
plt.xlim([-10, 50])
plt.tight_layout()

plt.show()

As it was already summarized by the R2 coefficient, we can see that the model fits the training data better than the test data, as indicated by the outliers in the y axis direction. Also, the distribution of the residuals does not seem to be completely random around the zero center point, indicating that the model is not able to capture all the exploratory information. However, the residual plot indicates a large improvement over the residual plot of the linear model that we plotted earlier in this chapter:

Summary

At the beginning of this chapter, you learned about using simple linear regression analysis to model the relationship between a single explanatory variable and a continuous response variable. We then discussed a useful explanatory data analysis technique to look at patterns and anomalies in data, which is an important first step in predictive modeling tasks.

We built our first model by implementing linear regression using a gradient-based optimization approach. We then saw how to utilize scikit-learn's linear models for regression and also implement a robust regression technique (RANSAC) as an approach for dealing with outliers. To assess the predictive performance of regression models, we computed the mean sum of squared errors and the related R2 metric. Furthermore, we also discussed a useful graphical approach to diagnose the problems of regression models: the residual plot.

After we discussed how regularization can be applied to regression models to reduce the model complexity and avoid overfitting, we also introduced several approaches to model nonlinear relationships, including polynomial feature transformation and random forest regressors.

We discussed supervised learning, classification, and regression analysis, in great detail throughout the previous chapters. In the next chapter, we are going to discuss another interesting subfield of machine learning: unsupervised learning. In the next chapter, you will learn how to use cluster analysis for finding hidden structures in data in the absence of target variables.

你可能感兴趣的:(cp10_回归预测连续目标变量_boston_Residual_plot_mlxtend_sns_pd_covariance_correlation_RANSAC_R2_Ridge_C_F_A_K_树)

QQ群采集助手，精准引流必备神器 2401_87347160 其他经验分享
功能概述微信群查找与筛选工具是一款专为微信用户设计的辅助工具，它通过关键词搜索功能，帮助用户快速找到相关的微信群，并提供筛选是否需要验证的群组的功能。主要功能关键词搜索：用户可以输入关键词，工具将自动查找包含该关键词的微信群。筛选功能：工具提供筛选机制，用户可以选择是否只显示需要验证或不需要验证的群组。精准引流：通过上述功能，用户可以更精准地找到目标群组，进行有效的引流操作。3.设备需求该工具可以
机器学习与深度学习间关系与区别 ℒℴѵℯ心·动ꦿ໊ོ꫞ 人工智能学习深度学习 python
一、机器学习概述定义机器学习（MachineLearning,ML）是一种通过数据驱动的方法，利用统计学和计算算法来训练模型，使计算机能够从数据中学习并自动进行预测或决策。机器学习通过分析大量数据样本，识别其中的模式和规律，从而对新的数据进行判断。其核心在于通过训练过程，让模型不断优化和提升其预测准确性。主要类型1.监督学习（SupervisedLearning）监督学习是指在训练数据集中包含输入
2020-01-25 晴岚85
郑海燕坚持分享590天2020.1.24在生活中只存在两个问题。一个问题是：你知道想要达成的目标是什么，但却不知道如何才能达成；另一个问题是：你不知道你的目标是什么。前一个是行动的问题，后一个是结果的问题。通过制定具体的下一步行动，可以解决不知道如何开始行动的问题。而通过去想象结果，对结果做预估，可以解决找不着目标的问题。对于所有吸引我们注意力，想要完成的任务，你可以先想象一下，预期的结果究竟是什
10月|愿你的青春不负梦想-读书笔记-01 Tracy的小书斋
本书的作者是俞敏洪，大家都很熟悉他了吧。俞敏洪老师是我行业的领头羊吧，也是我事业上的偶像。本日摘录他书中第一章中的金句：『一个人如果什么目标都没有，就会浑浑噩噩，感觉生命中缺少能量。能给我们能量的，是对未来的期待。第一件事，我始终为了进步而努力。与其追寻全世界的骏马，不如种植丰美的草原，到时骏马自然会来。第二件事，我始终有阶段性的目标。什么东西能给我能量？答案是对未来的期待。』读到这里的时候，我便
我校举行新老教师师徒结对仪式暨名师专业工作室工作交流活动李蕾1229
为促进我校教师专业发展，发挥骨干教师的引领带头作用，11月6日下午，我校举行新老教师师徒结对仪式暨名师专业工作室工作交流活动。图片发自App会议由教师发展处李蕾主任主持，首先，由范校长宣读新老教师结对名单及双方承担职责。随后，两位新调入教师陈玉萍、莫正杰分别和他们的师傅鲍元美、刘召彬老师签订了师徒结对协议书。图片发自App图片发自App师徒拥抱、握手。有了师傅就有了目标有了方向，相信两位新教师在师
第一场雪岁月静好_nx
早晨起来，外面白茫茫的一片，总算是下雪了，这还是今年第一场雪呢！走在路上，踩着雪“咯吱咯吱”的，空气很湿润。树上、草坪上、屋顶上都落了白白的一层，天上还零星漂着几点雪。慢慢走在路上，呼吸着清新的空气，感受着冬天的美好，心情也好多了。
开心蒋泳频
从无比抗拒来上课到接受，感动，收获～看着波哥成长，晶晶幸福笑容满面。感觉自己做的事情很有意义，很开心！还有3个感召目标就是还有三个有缘人，哈哈。明天感召去明日计划：8：30-11：00小公益11：00-21点上班，感召图片发自App图片发自App图片发自App
Python中os.environ基本介绍及使用方法鹤冲天Pro #Python python 服务器开发语言
文章目录python中os.environos.environ简介os.environ进行环境变量的增删改查python中os.environ的使用详解1.简介2.key字段详解2.1常见key字段3.os.environ.get()用法4.环境变量的增删改查和判断是否存在4.1新增环境变量4.2更新环境变量4.3获取环境变量4.4删除环境变量4.5判断环境变量是否存在python中os.envi
python os.environ_python os.environ 读取和设置环境变量 weixin_39605414 python os.environ
>>>importos>>>os.environ.keys()['LC_NUMERIC','GOPATH','GOROOT','GOBIN','LESSOPEN','SSH_CLIENT','LOGNAME','USER','HOME','LC_PAPER','PATH','DISPLAY','LANG','TERM','SHELL','J2REDIR','LC_MONETARY','QT_QPA
山东大学小树林支教调研团青青仓木队——翟晓楠山东大学青青仓木队
过了半年，又一次启程，又一次回到支教的初心之地。比起上一次的试探与不安，我更多了一丝稳重与熟练。心境、处境也都随着半个学期的过去而变得不同，半个学期中，身体上的，心理上的，太多的逆境让我变得步履维艰，曲曲折折，弯弯绕绕，我仿佛打不起精神，没有胃口，没有动力。感觉走的不顺畅的时候，支教这个旅程，给了我力量。自告奋勇承担起队长这一职务的我，从组织时的复杂和困难的经历，协调各种问题，从无到有，和校长和队
2018/02/12 Tracy_zhang
人生并不在于获取，更在于放得下。放下一粒种子，收获一棵大树;放下一处烦恼，收获一个惊喜;放下一种偏见，收获一种幸福;放下一种执著，收获一种自在。放下既是一种理性抉择，也是一种豁达美。只要看得开放得下，何愁没有快乐的春莺在啼鸣，何愁没有快乐的泉溪在歌唱，何愁没有快乐的鲜花绽放!
SQL Server_查询某一数据库中的所有表的内容 qq_42772833 SQL Server 数据库 sqlserver
1.查看所有表的表名要列出CrabFarmDB数据库中的所有表（名），可以使用以下SQL语句：USECrabFarmDB;--切换到目标数据库GOSELECTTABLE_NAMEFROMINFORMATION_SCHEMA.TABLESWHERETABLE_TYPE='BASETABLE';对这段SQL脚本的解释：SELECTTABLE_NAME：这个语句的作用是从查询结果中选择TABLE_NAM
高端密码学院笔记285 柚子_b4b4
高端幸福密码学院（高级班）幸福使者：李华第（598）期《幸福》之回归内在深层生命原动力基础篇——揭秘“激励”成长的喜悦心理案例分析主讲：刘莉一，知识扩充:成功=艰苦劳动+正确方法+少说空话。贪图省力的船夫，目标永远下游。智者的梦再美，也不如愚人实干的脚印。幸福早课堂2020.10.16星期五一笔记:1，重视和珍惜的前提是知道它的价值非常重要，当你珍惜了，你就真正定下来，真正的学到身上。2，大家需要
从0到500+，我是如何利用自媒体赚钱？一列脚印
运营公众号半个多月，从零基础的小白到现在慢慢懂了一些运营的知识。做好公众号是很不容易的，要做很多事情；排版、码字、引流…通通需要自己解决，业余时间全都花费在这上面涨这么多粉丝是真的不容易，对比知乎大佬来说，我们这种没资源，没人脉，还没钱的小透明来说，想要一个月涨粉上万，怕是今天没睡醒（不过你有的方法，算我piapia打脸）至少我是清醒的，自己慢慢努力，实现我的万粉目标！大家快来围观、支持我吧！孩子
春季养肝正当时 dxn悟
重温快乐2023年2月4日立春。春天来了，春暖花开，小鸟欢唱，那在这样的季节我们如何养肝呢？自然界的春季对应中医五行的木，人体五脏肝属木，“木曰曲直”，是以树干曲曲直直地向上、向外伸长舒展的生发姿态，来形容具有生长、升发、条达、舒畅等特征的食物及现象。根据中医天人相应的理念，肝五行属木，喜条达，主疏泄，与春天相应，所以春天最适合养肝。养肝首先要少生气，因为肝喜条达恶抑郁。人体五志肝为怒，生气发怒最
Day17笔记-高阶函数 ~在杰难逃~ Python 笔记 python 开发语言 pycharm 数据分析
高阶函数【重点掌握】函数的本质：函数是一个变量，函数名是一个变量名，一个函数可以作为另一个函数的参数或返回值使用如果A函数作为B函数的参数，B函数调用完成之后，会得到一个结果，则B函数被称为高阶函数常用的高阶函数：map(),reduce(),filter(),sorted()1.map()map(func,iterable)，返回值是一个iterator【容器，迭代器】func:函数iterab
读书||陶新华《教育中的积极心理学》1—28 流水淙淙2022
读一本好书，尤如和一位高尚者对话，亦能对人的精神进行洗礼。但是若不能和实践结合起来，也只能落到空读书的状态。读书摘要与感想1、塞利格曼在《持续的幸福》一书中提出了幸福2.0理论，提出幸福由5个元素决定——积极情绪、投入的工作和生活、目标和意义、和谐的人际关系、成就感。2、人的大脑皮层在进行智力活动时，都伴有皮下中枢活动，对这些活动进行体验请假，并由此产生了情感解读。人的情绪情感体验总是优先于大脑的
python八股文面试题分享及解析(1) Shawn________ python
#1.'''a=1b=2不用中间变量交换a和b'''#1.a=1b=2a,b=b,aprint(a)print(b)结果：21#2.ll=[]foriinrange(3):ll.append({'num':i})print(11)结果:#[{'num':0},{'num':1},{'num':2}]#3.kk=[]a={'num':0}foriinrange(3):#0,12#可变类型，不仅仅改变
【目标检测数据集】卡车数据集1073张VOC+YOLO格式熬夜写代码的平头哥∰ 目标检测 YOLO 人工智能
数据集格式：PascalVOC格式+YOLO格式(不包含分割路径的txt文件，仅仅包含jpg图片以及对应的VOC格式xml文件和yolo格式txt文件)图片数量(jpg文件个数)：1073标注数量(xml文件个数)：1073标注数量(txt文件个数)：1073标注类别数：1标注类别名称:["truck"]每个类别标注的框数：truck框数=1120总框数：1120使用标注工具：labelImg标注
MYSQL面试系列-04 king01299 面试 mysql 面试
MYSQL面试系列-0417.关于redolog和binlog的刷盘机制、redolog、undolog作用、GTID是做什么的？innodb_flush_log_at_trx_commit及sync_binlog参数意义双117.1innodb_flush_log_at_trx_commit该变量定义了InnoDB在每次事务提交时，如何处理未刷入（flush）的重做日志信息（redolog）。它
人生的每一步路都算数 sheli
如果你想打工，一直靠打工赚钱，那你就会不断的希望自己变得更专业，不断的希望能够获得更好的工作机会，升职加薪。如果你的目标志不在此，而是拥有自己的企业，那你的选择就会出现差别。在认真打工的人眼里，会“不务正业”，会总是选择不同岗位，甚至放弃高薪机会。但是这背后都是有更加长远的规划。成功富人所必需的管理技能包括：1．对现金流的管理。2．对系统的管理。3．对人员的管理。所以，在没有获得这些能力之前，只要
每日算法&面试题，大厂特训二十八天——第二十天（树）肥学 ⚡算法题⚡面试题每日精进 java 算法数据结构
目录标题导读算法特训二十八天面试题点击直接资料领取导读肥友们为了更好的去帮助新同学适应算法和面试题，最近我们开始进行专项突击一步一步来。上一期我们完成了动态规划二十一天现在我们进行下一项对各类算法进行二十八天的一个小总结。还在等什么快来一起肥学进行二十八天挑战吧！！特别介绍小白练手专栏，适合刚入手的新人欢迎订阅编程小白进阶python有趣练手项目里面包括了像《机器人尬聊》《恶搞程序》这样的有趣文章
Python快速入门 —— 第三节：类与对象孤华暗香 Python快速入门 python 开发语言
第三节：类与对象目标：了解面向对象编程的基础概念，并学会如何定义类和创建对象。内容：类与对象：定义类：class关键字。类的构造函数：__init__()。类的属性和方法。对象的创建与使用。示例：classStudent:def__init__(self,name,age,major):self.name&#
番茄西红柿叶子病害分类数据集12882张11类别 futureflsl 数据集分类数据挖掘人工智能
数据集类型：图像分类用，不可用于目标检测无标注文件数据集格式：仅仅包含jpg图片，每个类别文件夹下面存放着对应图片图片数量(jpg文件个数)：12882分类类别数：11类别名称:["Bacterial_Spot_Bacteria","Early_Blight_Fungus","Healthy","Late_Blight_Water_Mold","Leaf_Mold_Fungus","Powdery
python os 环境变量 CV矿工 python 开发语言 numpy
环境变量：环境变量是程序和操作系统之间的通信方式。有些字符不宜明文写进代码里，比如数据库密码，个人账户密码，如果写进自己本机的环境变量里，程序用的时候通过os.environ.get（）取出来就行了。os.environ是一个环境变量的字典。环境变量的相关操作importos"""设置/修改环境变量：os.environ[‘环境变量名称’]=‘环境变量值’#其中key和value均为string类
Python爬虫解析工具之xpath使用详解 eqa11 python 爬虫开发语言
文章目录Python爬虫解析工具之xpath使用详解一、引言二、环境准备1、插件安装2、依赖库安装三、xpath语法详解1、路径表达式2、通配符3、谓语4、常用函数四、xpath在Python代码中的使用1、文档树的创建2、使用xpath表达式3、获取元素内容和属性五、总结Python爬虫解析工具之xpath使用详解一、引言在Python爬虫开发中，数据提取是一个至关重要的环节。xpath作为一门
2018-12-29 枫叶红时总多离别
2018年12月29日星期六昨天老师就告诉我们，今天下午不用上课，是图书漂流活动会。我觉得很兴奋，好期待。到了下午，我帮好忙就到外面去买书，刚一出去，就有一大帮的大哥哥、大姐姐围着我问要不要买书，买一本书送一颗糖。我看到了一本《小老虎比上树》的书，问大姐姐多少钱，大姐姐说这本书原价13块，现在便宜4块钱也就是9块钱卖给你，我就把一张10块钱给她找，她找了我一块钱。我现在想想我今天只带了10块钱，现
ARM驱动学习之5 LEDS驱动 JT灬新一嵌入式 C 底层 arm开发学习单片机
ARM驱动学习之5LEDS驱动知识点：•linuxGPIO申请函数和赋值函数–gpio_request–gpio_set_value•三星平台配置GPIO函数–s3c_gpio_cfgpin•GPIO配置输出模式的宏变量–S3C_GPIO_OUTPUT注意点：DRIVER_NAME和DEVICE_NAME匹配。实现步骤：1.加入需要的头文件：//Linux平台的gpio头文件#include//三
Low Power概念介绍-Voltage Area 飞奔的大虎
随着智能手机，以及物联网的普及，芯片功耗的问题最近几年得到了越来越多的重视。为了实现集成电路的低功耗设计目标，我们需要在系统设计阶段就采用低功耗设计的方案。而且，随着设计流程的逐步推进，到了芯片后端设计阶段，降低芯片功耗的方法已经很少了，节省的功耗百分比也不断下降。芯片的功耗主要由静态功耗（staticleakagepower）和动态功耗(dynamicpower)构成。静态功耗主要是指电路处于等
基于CODESYS的多轴运动控制程序框架：逻辑与运动控制分离，快速开发灵活操作 GPJnCrbBdl python 开发语言
基于codesys开发的多轴运动控制程序框架，将逻辑与运动控制分离，将单轴控制封装成功能块，对该功能块的操作包含了所有的单轴控制（归零、点动、相对定位、绝对定位、设置当前位置、伺服模式切换等等）。程序框架由主程序按照状态调用分归零模式、手动模式、自动模式、故障模式，程序状态的跳转都已完成，只需要根据不同的工艺要求完成所需的动作即可。变量的声明、地址的规划都严格按照C++的标准定义，能帮助开发者快速
桌面上有多个球在同时运动，怎么实现球之间不交叉，即碰撞？换个号韩国红果果 html 小球碰撞
稍微想了一下，然后解决了很多bug，最后终于把它实现了。其实原理很简单。在每改变一个小球的x y坐标后，遍历整个在dom树中的其他小球，看一下它们与当前小球的距离是否小于球半径的两倍？若小于说明下一次绘制该小球（设为a）前要把他的方向变为原来相反方向（与a要碰撞的小球设为b），即假如当前小球的距离小于球半径的两倍的话，马上改变当前小球方向。那么下一次绘制也是先绘制b，再绘制a，由于a的方向已经改变
《高性能HTML5》读后整理的Web性能优化内容白糖_ html5
读后感先说说《高性能HTML5》这本书的读后感吧，个人觉得这本书前两章跟书的标题完全搭不上关系，或者说只能算是讲解了“高性能”这三个字，HTML5完全不见踪影。个人觉得作者应该首先把HTML5的大菜拿出来讲一讲，再去分析性能优化的内容，这样才会有吸引力。因为只是在线试读，没有机会看后面的内容，所以不胡乱评价了。
[JShop]Spring MVC的RequestContextHolder使用误区 dinguangx jeeshop 商城系统 jshop 电商系统
在spring mvc中，为了随时都能取到当前请求的request对象，可以通过RequestContextHolder的静态方法getRequestAttributes()获取Request相关的变量，如request, response等。在jshop中，对RequestContextHolder的
算法之时间复杂度周凡杨 java 算法时间复杂度效率
在计算机科学中，算法的时间复杂度是一个函数，它定量描述了该算法的运行时间。这是一个关于代表算法输入值的字符串的长度的函数。时间复杂度常用大O符号表述，不包括这个函数的低阶项和首项系数。使用这种方式时，时间复杂度可被称为是渐近的，它考察当输入值大小趋近无穷时的情况。这样用大写O()来体现算法时间复杂度的记法，
Java事务处理 g21121 java
一、什么是Java事务通常的观念认为，事务仅与数据库相关。事务必须服从ISO/IEC所制定的ACID原则。ACID是原子性（atomicity）、一致性（consistency）、隔离性（isolation）和持久性（durability）的缩写。事务的原子性表示事务执行过程中的任何失败都将导致事务所做的任何修改失效。一致性表示当事务执行失败时，所有被该事务影响的数据都应该恢复到事务执行前的状
Linux awk命令详解 510888780 linux
一. AWK 说明 awk是一种编程语言，用于在linux/unix下对文本和数据进行处理。数据可以来自标准输入、一个或多个文件，或其它命令的输出。它支持用户自定义函数和动态正则表达式等先进功能，是linux/unix下的一个强大编程工具。它在命令行中使用，但更多是作为脚本来使用。 awk的处理文本和数据的方式：它逐行扫描文件，从第一行到
android permission 布衣凌宇 Permission
<uses-permission android:name="android.permission.ACCESS_CHECKIN_PROPERTIES" ></uses-permission>允许读写访问"properties"表在checkin数据库中，改值可以修改上传 <uses-permission android:na
Oracle和谷歌Java Android官司将推迟 aijuans java oracle
北京时间 10 月 7 日，据国外媒体报道，Oracle 和谷歌之间一场等待已久的官司可能会推迟至 10 月 17 日以后进行，这场官司的内容是 Android 操作系统所谓的 Java 专利权之争。本案法官 William Alsup 称根据专利权专家 Florian Mueller 的预测，谷歌 Oracle 案很可能会被推迟。　　该案中的第二波辩护被安排在 10 月 17 日出庭，从目前看来
linux shell 常用命令 antlove linux shell command
grep [options] [regex] [files] /var/root # grep -n "o" * hello.c:1:/* This C source can be compiled with:
Java解析XML配置数据库连接(DOM技术连接 SAX技术连接) 百合不是茶 sax技术 Java解析xml文档 dom技术 XML配置数据库连接
XML配置数据库文件的连接其实是个很简单的问题,为什么到现在才写出来主要是昨天在网上看了别人写的,然后一直陷入其中,最后发现不能自拔所以今天决定自己完成 ,,,,现将代码与思路贴出来供大家一起学习 XML配置数据库的连接主要技术点的博客; JDBC编程 : JDBC连接数据库 DOM解析XML: DOM解析XML文件 SA
underscore.js 学习（二） bijian1013 JavaScript underscore
Array Functions 所有数组函数对参数对象一样适用。1.first _.first(array, [n]) 别名: head, take 返回array的第一个元素，设置了参数n，就
plSql介绍 bijian1013 oracle 数据库 plsql
/* * PL/SQL 程序设计学习笔记 * 学习plSql介绍.pdf * 时间：2010-10-05 */ --创建DEPT表 create table DEPT ( DEPTNO NUMBER(10), DNAME NVARCHAR2(255), LOC NVARCHAR2(255) ) delete dept; select
【Nginx一】Nginx安装与总体介绍 bit1129 nginx
启动、停止、重新加载Nginx nginx 启动Nginx服务器，不需要任何参数u nginx -s stop 快速(强制)关系Nginx服务器 nginx -s quit 优雅的关闭Nginx服务器 nginx -s reload 重新加载Nginx服务器的配置文件 nginx -s reopen 重新打开Nginx日志文件
spring mvc开发中浏览器兼容的奇怪问题 bitray jquery Ajax springMVC 浏览器上传文件
最近个人开发一个小的OA项目,属于复习阶段.使用的技术主要是spring mvc作为前端框架,mybatis作为数据库持久化技术.前台使用jquery和一些jquery的插件. 在开发到中间阶段时候发现自己好像忽略了一个小问题,整个项目一直在firefox下测试,没有在IE下测试,不确定是否会出现兼容问题.由于jquer
Lua的io库函数列表 ronin47 lua io
1、io表调用方式：使用io表，io.open将返回指定文件的描述，并且所有的操作将围绕这个文件描述　　io表同样提供三种预定义的文件描述io.stdin,io.stdout,io.stderr 　　2、文件句柄直接调用方式,即使用file:XXX()函数方式进行操作,其中file为io.open()返回的文件句柄　　多数I/O函数调用失败时返回nil加错误信息,有些函数成功时返回nil
java-26-左旋转字符串 bylijinnan java
public class LeftRotateString { /** * Q 26 左旋转字符串 * 题目：定义字符串的左旋转操作：把字符串前面的若干个字符移动到字符串的尾部。 * 如把字符串abcdef左旋转2位得到字符串cdefab。 * 请实现字符串左旋转的函数。要求时间对长度为n的字符串操作的复杂度为O(n)，辅助内存为O(1)。 */ pu
《vi中的替换艺术》-linux命令五分钟系列之十一 cfyme linux命令
vi方面的内容不知道分类到哪里好，就放到《Linux命令五分钟系列》里吧！今天编程，关于栈的一个小例子，其间我需要把”S.”替换为”S->”(替换不包括双引号)。其实这个不难，不过我觉得应该总结一下vi里的替换技术了，以备以后查阅。 1 所有替换方案都要在冒号“:”状态下书写。 2 如果想将abc替换为xyz，那么就这样 :s/abc/xyz/ 不过要特别
[轨道与计算]新的并行计算架构 comsci 并行计算
我在进行流程引擎循环反馈试验的过程中，发现一个有趣的事情。。。如果我们在流程图的每个节点中嵌入一个双向循环代码段，而整个流程中又充满着很多并行路由，每个并行路由中又包含着一些并行节点，那么当整个流程图开始循环反馈过程的时候，这个流程图的运行过程是否变成一个并行计算的架构呢？
重复执行某段代码 dai_lm android
用handler就可以了 private Handler handler = new Handler(); private Runnable runnable = new Runnable() { public void run() { update(); handler.postDelayed(this, 5000); } }; 开始计时 h
Java实现堆栈（list实现） datageek 数据结构——堆栈
public interface IStack<T> { //元素出栈，并返回出栈元素 public T pop(); //元素入栈 public void push(T element); //获取栈顶元素 public T peek(); //判断栈是否为空 public boolean isEmpty
四大备份MySql数据库方法及可能遇到的问题 dcj3sjt126com DB backup
一：通过备份王等软件进行备份前台进不去？用备份王等软件进行备份是大多老站长的选择，这种方法方便快捷，只要上传备份软件到空间一步步操作就可以，但是许多刚接触备份王软件的客用户来说还原后会出现一个问题：因为新老空间数据库用户名和密码不统一，网站文件打包过来后因没有修改连接文件，还原数据库是好了，可是前台会提示数据库连接错误，网站从而出现打不开的情况。解决方法：学会修改网站配置文件，大多是由co
github做webhooks：[1]钩子触发是否成功测试 dcj3sjt126com github git webhook
转自: http://jingyan.baidu.com/article/5d6edee228c88899ebdeec47.html github和svn一样有钩子的功能，而且更加强大。例如我做的是最常见的push操作触发的钩子操作，则每次更新之后的钩子操作记录都会在github的控制板可以看到！工具/原料 github 方法/步骤
">的作用" target="_blank">JSP中的作用蕃薯耀
JSP中<base href="<%=basePath%>">的作用 >>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>
linux下SAMBA服务安装与配置 hanqunfeng linux
局域网使用的文件共享服务。一.安装包： rpm -qa | grep samba samba-3.6.9-151.el6.x86_64 samba-common-3.6.9-151.el6.x86_64 samba-winbind-3.6.9-151.el6.x86_64 samba-client-3.6.9-151.el6.x86_64 samba-winbind-clients
guava cache IXHONG cache
缓存，在我们日常开发中是必不可少的一种解决性能问题的方法。简单的说，cache 就是为了提升系统性能而开辟的一块内存空间。　　缓存的主要作用是暂时在内存中保存业务系统的数据处理结果，并且等待下次访问使用。在日常开发的很多场合，由于受限于硬盘IO的性能或者我们自身业务系统的数据处理和获取可能非常费时，当我们发现我们的系统这个数据请求量很大的时候，频繁的IO和频繁的逻辑处理会导致硬盘和CPU资源的
Query的开始--全局变量,noconflict和兼容各种js的初始化方法 kvhur JavaScript jquery css
这个是整个jQuery代码的开始，里面包含了对不同环境的js进行的处理，例如普通环境，Nodejs，和requiredJs的处理方法。还有jQuery生成$, jQuery全局变量的代码和noConflict代码详解完整资源： http://www.gbtags.com/gb/share/5640.htm jQuery 源码： (
美国人的福利和中国人的储蓄 nannan408
今天看了篇文章，震动很大，说的是美国的福利。美国医院的无偿入院真的是个好措施。小小的改善，对于社会是大大的信心。小孩，税费等，政府不收反补，真的体现了人文主义。美国这么高的社会保障会不会使人变懒？答案是否定的。正因为政府解决了后顾之忧，人们才得以倾尽精力去做一些有创造力，更造福社会的事情，这竟成了美国社会思想、人
N阶行列式计算(JAVA) qiuwanchi N阶行列式计算
package gaodai; import java.util.List; /** * N阶行列式计算 * @author 邱万迟 * */ public class DeterminantCalculation { public DeterminantCalculation(List<List<Double>> determina
C语言算法之打渔晒网问题 qiufeihu c 算法
如果一个渔夫从2011年1月1日开始每三天打一次渔，两天晒一次网，编程实现当输入2011年1月1日以后任意一天，输出该渔夫是在打渔还是在晒网。代码如下： #include <stdio.h> int leap(int a) /*自定义函数leap()用来指定输入的年份是否为闰年*/ { if((a%4 == 0 && a%100 != 0
XML中DOCTYPE字段的解析 wyzuomumu xml
DTD声明始终以!DOCTYPE开头,空一格后跟着文档根元素的名称,如果是内部DTD,则再空一格出现[],在中括号中是文档类型定义的内容. 而对于外部DTD,则又分为私有DTD与公共DTD,私有DTD使用SYSTEM表示,接着是外部DTD的URL. 而公共DTD则使用PUBLIC,接着是DTD公共名称,接着是DTD的URL. 私有DTD <!DOCTYPErootSYST