cp2_TrainingSimpleMachineLearningAlgorithmsForClassification_meshgrid_ravel_contourf_OvA_GradientDes
we will make use of one of the first algorithmically described machine learning algorithms for classification, the perceptron感知器 and adaptive linear neurons自适应线性神经元. We will start by implementing a perceptron step by step in Python and training it to classify different flower species in the Iris dataset. This will help us to understand the concept of machine learning algorithms for classification and how they can be efficiently implemented in Python. Discussing the basics of optimization using adaptive linear neurons will then lay the groundwork for using more powerful
classifiers via the scikit-learn machine-learning library in Cp3:
https://blog.csdn.net/Linli522362242/article/details/96480059, A Tour of Machine Learning Classifiers Using Scikit-learn.
The topics that we will cover in this chapter are as follows:
- Building an intuition for machine learning algorithms
- Using pandas, NumPy, and matplotlib to read in, process, and visualize data
- Implementing linear classification algorithms in Python
Artificial neurons [ˈnʊrɑn]神经元 – a brief glimpse into the early history of machine learning
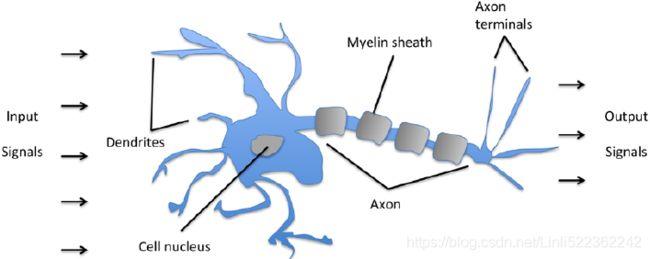
Neurons are interconnected nerve cells in the brain that are involved in the processing and transmitting of chemical and electrical signals, which is illustrated in the following figure:
McCullock and Pitts described such a nerve cell as a simple logic gate with binary outputs; multiple signals arrive at the dendrites[ˈdɛnˌdraɪt] 树突, are then integrated into the cell body, and, if the accumulated signal exceeds a certain threshold阀值, an output signal is generated that will be passed on by the axon [ˈæksiˌɑn]轴突.
Only a few years later, Frank Rosenblatt published the first concept of the perceptron感知器 learning rule based on the MCP neuron model (F. Rosenblatt, The Perceptron, a Perceiving and Recognizing Automaton. Cornell Aeronautical Laboratory, 1957). With his perceptron rule, Rosenblatt proposed an algorithm that would automatically learn the optimal weight coefficients that are then multiplied with the input features in order to make the decision of whether a neuron fires or not. In the context of supervised learning and classification, such an algorithm could then be used to predict if a sample belonged to one class or the other.
The formal definition of an artificial neuron
More formally, we can pose this problem as a binary classification task where we refer to our two classes as 1 (positive class) and -1 (negative class) for simplicity. We can then define an activation function激活函数 
that takes a linear combination of certain input values x and a corresponding weight vector w , where z is the so-called net input ( 
):
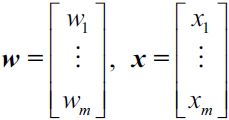
Now, if the activation of a particular sample 
, that is, the output of , is greater than a defined threshold 
, we predict class 1 and class -1, otherwise. In the perceptron algorithm, the activation function 
is a simple unit step分段 function, which is sometimes also called the Heaviside海维赛德 step function:
For simplicity, we can bring the threshold to the left side of the equation( z - 
0) and define a weight-zero as 
= − and 
=1, so that we write in a more compact form 
and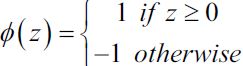 
.
In machine learning literature, the negative threshold, or weight, 
, is usually called the bias unit.
###################################
Note
In the following sections, we will often make use of basic notations from linear algebra. For example, we will abbreviate the sum of the products of the values in x and w using a vector dot product, whereas superscript T stands for transpose, which is an operation that transforms a column vector into a row vector and vice versa:
Furthermore, the transpose operation can also be applied to a matrix to reflect it over its diagonal, for example: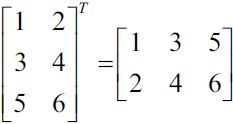
we will only use very basic concepts from linear algebra; however, if you need a quick refresher, please take a look at Zico Kolter's excellent Linear Algebra Review and Reference, which is freely available at http://www.cs.cmu.edu/~zkolter/course/linalg/linalg_notes.pdf
###################################
The following figure illustrates how the net input 
is squashed挤压 into a binary output (-1 or 1) by the activation function of the perceptron (left subfigure) and how it can be used to discriminate区别 between two linearly separable classes (right subfigure):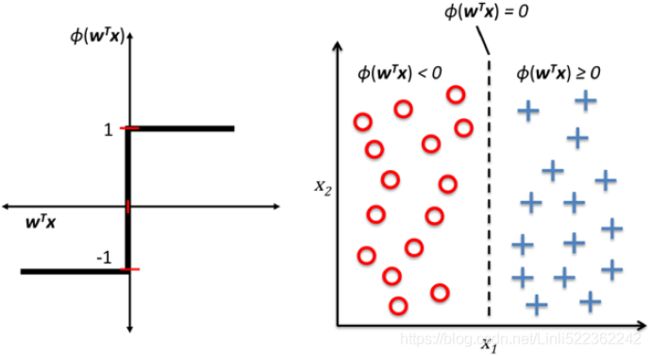
The perceptron learning rule
The whole idea behind the MCP(McCullock-Pitts) neuron and Rosenblatt's thresholded perceptron model is to use a reductionist还原论 approach to mimic how a single neuron in the brain works: it either fires or it doesn't. Thus, Rosenblatt's initial perceptron rule is fairly simple and can be summarized by the following steps:
1. Initialize the weights to 0 or small random numbers.
2. For each training sample perform the following steps:
1. Compute the output value 
.
2. Update the weights.
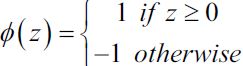Here, the output value is the predicted class label predicted by the unit step function, that we defined earlier, and the simultaneous update of each weight 
in the weight vector w can be more formally written as: 
# j is the feature index or the dimension index
The value of 
, which is used to update the weight 
, is calculated by the perceptron learning rule:
# i is the instance index
Where 
is the learning rate (a constant between 0.0 and 1.0), 
is the true class label of the ith training sample, and 
is the predicted class label. It is important to note that all weights in the weight vector are being updated simultaneously, which means that we don't recompute the output value (or 
) before all of the weights 
were updated. Concretely, for a 2D dataset, we would write the update as follows:
Before we implement the perceptron rule in Python, let us make a simple thought experiment to illustrate how beautifully simple this learning rule really is. In the two scenarios where the perceptron predicts the class label correctly, the weights remain unchanged: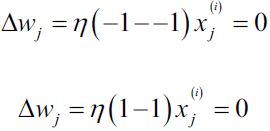
However, in the case of a wrong prediction, the weights are being pushed towards the direction of the positive or negative target class, respectively: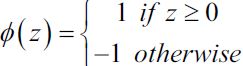
since the true class label is +1, the predicted class label is -1, then
-->increasing the value of 
--> increasing-->increasing--> until z>=0; ; 
and 
=1
since the true class label is -1, the predicted class label is +1, then
-->reducing the value of -->decreasing -->decreasing-->until z<0; ; 
and =1
To get a better intuition for the multiplicative factor
, let us go through another simple example, where: 
Let's assume that 
, and we misclassify this sample as -1. In this case, we would increase the corresponding weight by 1 ### = 1*(1-(-1))*0.5==1--> ###so that the net input 
would be more positive the next time we encounter this sample, and thus be more likely to be above the threshold of the unit step function to classify the sample as +1: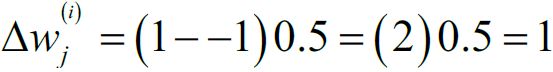 
The weight update is proportional to the value of 
. For example, if we have another sample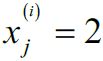 
that is incorrectly classified as -1, we'd push the decision boundary by an even larger extent to classify this sample correctly the next time: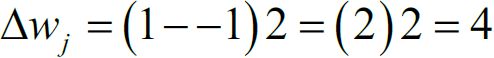 
It is important to note that the convergence of the perceptron is only guaranteed if the two classes are linearly separable and the learning rate is sufficiently small. If the two classes can't be separated by a linear decision boundary, we can set a maximum number of passes over the training dataset (epochs迭代次数) and/or a threshold for the number of tolerated misclassifications—the perceptron would never stop updating the weights otherwise: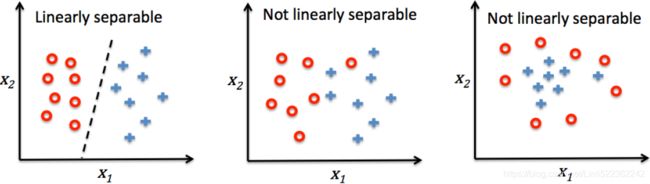
Now, before we jump into the implementation in the next section, let us summarize what we just learned in a simple figure that illustrates the general concept of the perceptron:
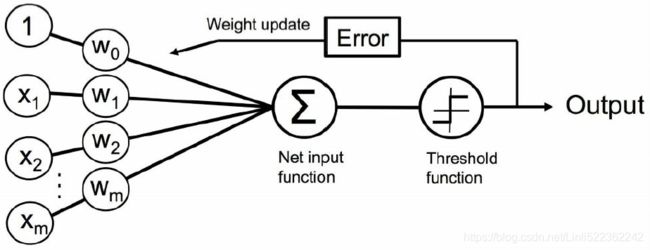
The preceding figure illustrates how the perceptron receives the inputs of a sample x and combines them with the weights w to compute the net input（）. The net input is then passed on to the activation function (here: the unit step function 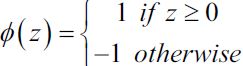), which generates a binary output -1 or +1—the predicted class label of the sample. During the learning phase, this output is used to calculate the error 
of the prediction and update the weights , .
Implementing a perceptron learning algorithm in Python
In the previous section, we learned how Rosenblatt's perceptron rule works; let us now go ahead and implement it in Python and apply it to the Iris dataset, Giving Computers the Ability to Learn from Data.
An object-oriented perceptron API
We will take an objected-oriented approach to define the perceptron interface as a Python Class, which allows us to initialize new perceptron objects that can learn from data via a fit method, and make predictions via a separate predict method. As a convention, we add an underscore (_) to attributes that are not being created upon the initialization of the object but by calling the object's other methods—for example, self.w_.
######################################
Note
If you are not yet familiar with Python's scientific libraries or need a refresher, please see the following resources:
NumPy: https://sebastianraschka.com/pdf/books/dlb/appendix_f_numpyintro.pdf
pandas: https://pandas.pydata.org/pandas-docs/stable/10min.html
Matplotlib: http://matplotlib.org/users/beginner.html
######################################
The following is the implementation of a perceptron:
import numpy as np
randomGenerator = np.random.RandomState(0)
weightVector = randomGenerator.normal( loc=0.0, scale=0.01, size=1+3 )
weightVector
class Perceptron(object):
def __init__(self, eta =0.01, n_iter=10, random_state=1):
self.eta = eta # float: Learning rate (between 0.0 and 1.0)
self.n_iter = n_iter # int : Passes over the training dataset
self.random_state = random_state # int : Random number generator seed for random weight initialization.
def fit(self, X, y): #y:Target values. #X:shape = [n_samples, n_features]
rgen = np.random.RandomState(self.random_state)
#正态分布的标准差，对应分布的宽度，scale/sigma越大，正态分布的曲线越矮胖，scale越小，曲线越高瘦
#mu #sigma #n_features
self.w_ = rgen.normal(loc=0.0, scale=0.01, size=1+X.shape[1]) #1:self.w_[0]
#If all the weights are initialized to zero, the learning rate parameter
#eta affects only the scale of the weight vector,########################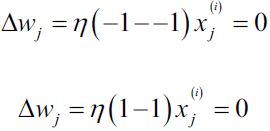
However, in the case of a wrong prediction, the weights are being pushed towards the direction of the positive or negative target class, respectively: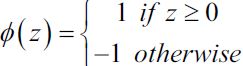
Now, the reason we don't initialize the weights to zero is that the learning rate 
(eta) only has an effect on the classification outcome if the weights are initialized to non-zero values( current ; next , larger -->larger
if 
=
-->larger 
, shift to the direction with larger z then affect the classification and the direction;
OR larger -->smallerif =
-->smaller, shift to the direction with smaller z then affect the classification).
If all the weights are initialized to zero, the learning rate parameter (eta) affects only the scale of the weight vector, not the direction/slope(does not exist shift or move action). If you are familiar with trigonometry, consider a vector 
, where the angle between 
and a vector 
would be exactly zero, as demonstrated by the following code snippet:
v1 = np.array([1, 2, 3])
v2 = 0.5 * v1 ###########=
#np.linalg.norm(v1) == np.sqrt(1**2 + 2**2 + 3**2)==3.7416573867739413
np.arccos(v1.dot(v2) / ( np.linalg.norm(v1) *np.linalg.norm(v2)) )
### In support vector machine, we will want to get a boundary line/separating hyperplane to separate classes,
### if we just want to get a boundary line, we will use weight to decide its position and slope/direction
Here, np.arccos is the trigonometric inverse cosine and np.linalg.norm is a function that computes the length of a vector.(The reason why we have drawn the random numbers from a random normal distribution—for example, instead from a uniform distribution—and why we used a standard deviation of 0.01 was arbitrary; remember, we are just interested in small random values to avoid the properties of all-zero vectors as discussed earlier.)
########################
# def fit(self, X, y): #y:Target values. #X:shape = [n_samples, n_features]
# rgen = np.random.RandomState(self.random_state)
#正态分布的标准差，对应分布的宽度，scale/sigma越大，正态分布的曲线越矮胖，scale越小，曲线越高瘦
#mu #sigma #n_features
# self.w_ = rgen.normal(loc=0.0, scale=0.01, size=1+X.shape[1]) #1:self.w_[0]
#If all the weights are initialized to zero, the learning rate parameter
#eta affects only the scale of the weight vector,
self.errors_ = [] #Number of misclassifications (updates) in each epoch.
for _ in range(self.n_iter):
errors = 0
for xi, target in zip(X,y): #xi_sample_vector, target_sample_label
#delta_weight_vector
update = self.eta * (target - self.predict(xi))
# updating the weights after evaluating each individual training sample,
# all weights += the result of (update * xi)
self.w_[1:] += update * xi # hidden: traverse and update the weights of all features
self.w_[0] += update
#print(self.w_)
errors += int(update !=0.0)
self.errors_.append(errors) #errors == all X_samples' error
return self
def net_input(self, X): # X_feature_vector * w^T
return np.dot(X, self.w_[1:]) + self.w_[0] #prediction=X(samples, features) dot W(features, 1)
def predict(self, X): #X_feature_vector
return np.where(self.net_input(X) >= 0.0, 1, -1) #classification Using this perceptron implementation, we can now initialize new Perceptron objects with a given learning rate eta and n_iter, which is the number of epochs (passes over the training set). Via the fit method we initialize the weights in self.w_ to a nonzero-vector 
where m stands for the number of dimensions (features) in the dataset, where we add 1 for the first element in this vector that represents the bias unit. Remember that the first element in this vector, self.w_[0], represents the so-called bias unit that we discussed earlier.
Also notice that this vector contains small random numbers drawn from a normal distribution with standard deviation 0.01 via rgen.normal(loc=0.0, scale=0.01, size=1 + X.shape[1]), where rgen is a NumPy random number generator( rgen = np.random.RandomState(self.random_state) ) that we seeded with a user-specified random seed so that we can reproduce previous results if desired.
##########################
Note
Instead of using NumPy to calculate the vector dot product between two arrays a and b via a.dot(b) or np.dot(a, b), we could also perform the calculation in pure Python via sum([ i * j for i, j in zip(a, b) ]). However, the advantage of using NumPy over classic Python for loop structures is that its arithmetic operations are vectorized. Vectorization means that an elemental arithmetic operation is automatically applied to all elements in an array. By formulating our arithmetic operations as a sequence of instructions on an array, rather than performing a set of operations for each element at the time, we can make better use of our modern CPU architectures with Single Instruction, Multiple Data (SIMD) support. Furthermore,
NumPy uses highly optimized linear algebra libraries such as Basic Linear Algebra Subprograms (BLAS) and Linear Algebra Package (LAPACK) that have been written in C or Fortran. Lastly, NumPy also allows us to write our code in a more compact and intuitive way using the basics of linear algebra, such as vector and matrix dot products.
##########################
Training a perceptron model on the Iris dataset
To test our perceptron implementation, we will load the two flower classes Setosa and Versicolor from the Iris dataset. Although the perceptron rule is not restricted to two dimensions, we will only consider the two features sepal length and petal length for visualization purposes. Also, we only chose the two flower classes Setosa and Versicolor for practical reasons. However, the perceptron algorithm can be extended to multi-class classification—for example, the One-versus-All (OvA) technique.
###############
Note
OvA, or sometimes also called One-versus-Rest (OvR), is a technique that allows us to extend a binary classifier to multi-class problems. Using OvA, we can train one classifier per class, where the particular class is treated as the positive class and the samples from all other classes are considered negative classes. If we were to classify a new data sample, we would use our n classifiers, where n is the number of class labels, and assign the class label with the highest confidence to the particular sample. In the case of the perceptron, we would use OvA to choose the class label that is
associated with the largest absolute net input value.
https://blog.csdn.net/Linli522362242/article/details/103786116
###############
First, we will use the pandas library to load the Iris dataset directly from the UCI Machine Learning Repository资料库(OR from sklearn import datasets; iris = datasets.load_iris() https://blog.csdn.net/Linli522362242/article/details/104097191) into a DataFrame object and print the last five lines via the tail method to check the data was loaded correctly:
import pandas as pd
df = pd.read_csv('L:/MachineLearningInAction/machine_learning_databases/iris/iris.data', header=None)
df.tail()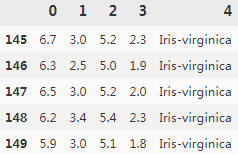
Next, we extract the first 100 class labels that correspond to the 50 Iris-Setosa and 50 Iris-Versicolor flowers, respectively, and convert the class labels into the two integer class labels 1 (Versicolor) and -1 (Setosa) that we assign to a vector y where the values method of a pandas DataFrame yields the corresponding NumPy representation. Similarly, we extract the first feature column (sepal length) and the third feature column (petal length) of those 100 training samples and assign them to a feature matrix X, which we can visualize via a two-dimensional scatter plot:
import matplotlib.pyplot as plt
import numpy as np
# select setosa and versicolor
y = df.iloc[0:100, 4].values # 4: the 4th column~class label
y = np.where(y=='Iris-setosa', -1, 1)
y
# extract sepal length and peta length
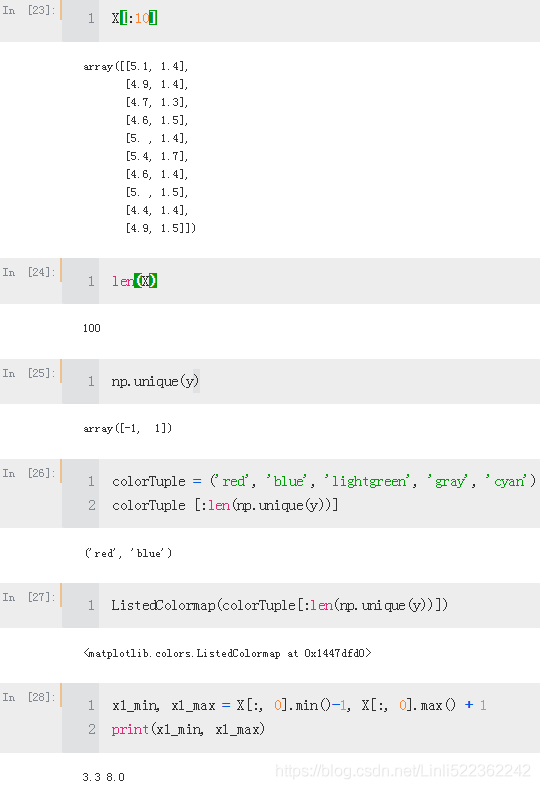
X = df.iloc[0:100, [0,2]].values
X[:5]
# plot data
plt.scatter(X[:50, 0], X[:50, 1], color='red', marker = 'o', label = 'setosa')
plt.scatter(X[50:100,0], X[50:100,1], color = 'blue', marker='x', label='versicolor')
plt.xlabel('sepal length [cm]')
plt.ylabel('petal length [cm]')
plt.legend(loc='upper left')
plt.show()After executing the preceding code example we should now see the following scatterplot:
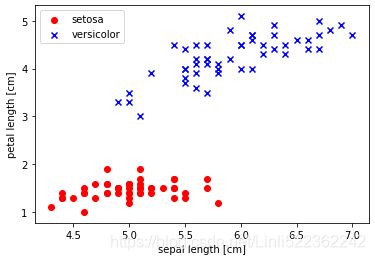
Now it's time to train our perceptron algorithm on the Iris data subset that we just extracted. Also, we will plot the misclassification error for each epoch to check if the algorithm converged and found a decision boundary that separates the two Iris flower classes:
ppn = Perceptron(eta=0.1, n_iter=10)
ppn.fit(X,y)
plt.plot(range(1, len(ppn.errors_) + 1), ppn.errors_, marker='o')
plt.xlabel('Epochs')
plt.ylabel('Number of updates') # the changes of weightVector
plt.show()After executing the preceding code, we should see the plot of the misclassification errors versus the number of epochs, as shown next:
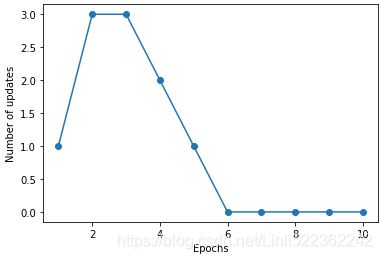
As we can see in the preceding plot, our perceptron already converged after the sixth epoch and should now be able to classify the training samples perfectly. Let us implement a small convenience function to visualize the decision boundaries for 2D datasets:
from matplotlib.colors import ListedColormap
def plot_decision_regions(X, y, classifier, resolution =0.02):
#setup marker generator and color map
markerTuple =('s', 'x', 'o', '^', 'v')
colorTuple = ('red', 'blue', 'lightgreen', 'gray', 'cyan')
# take 'red' and 'blue'
cmap = ListedColormap( colorTuple[:len(np.unique(y))] ) #从颜色列表生成的颜色映射对象
#plot the decision surface
x1_min, x1_max = X[:, 0].min()-1, X[:, 0].max() + 1
x2_min, x2_max = X[:, 1].min()-1, X[:, 1].max() + 1
#step #rows==len(secondParaArr) cols=len(firstParaArr)
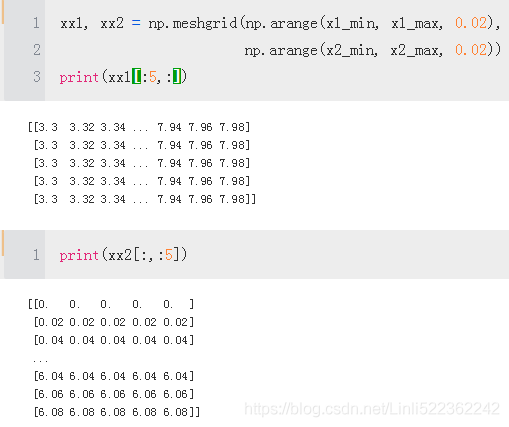
xx1, xx2 = np.meshgrid(np.arange(x1_min, x1_max, resolution), #horizontal and be filled row by row
np.arange(x2_min, x2_max, resolution)) #vertical and be filled column by column
#ravel(): one dimension array and column wise(order='C')
#np.array(): two dimension
Z = classifier.predict(np.array([xx1.ravel(), xx2.ravel()]).T)
# Z = classifier.predict( np.c_[xx1.ravel(), xx2.ravel()] )
Z = Z.reshape(xx1.shape)
plt.contourf(xx1, xx2, Z, alpha=0.3, cmap=cmap)
plt.xlim(xx1.min(), xx1.max()) #sepal length or x-axis or feature
plt.ylim(xx2.min(), xx2.max()) #petal length or y-axis or feature
#plot class samples
for idx, cl in enumerate(np.unique(y)):
#0 -1
#1 1
plt.scatter(x=X[y==cl, 0],
y=X[y==cl, 1],
alpha=0.8,
c=colorTuple[idx],
marker=markerTuple[idx],
label=cl,
edgecolor='black')First, we define a number of colors and markers and create a color map from the list of colors via ListedColormap. Then, we determine the minimum and maximum values for the two features and use those feature vectors to create a pair of grid arrays xx1 and xx2 via the NumPy meshgrid function. Since we trained our perceptron classifier on two feature dimensions, we need to flatten the grid arrays and create a matrix that has the same number of columns as the Iris training subset so that we can use the predict method to predict the class labels Z of the corresponding grid points. After reshaping the predicted class labels Z into a grid with the same dimensions as xx1 and xx2, we can now draw a contour plot via matplotlib's contourf function that maps the different decision regions to different colors for each predicted class in the grid array:
#ppn = Perceptron(eta=0.1, n_iter=10)
#ppn.fit(X,y)
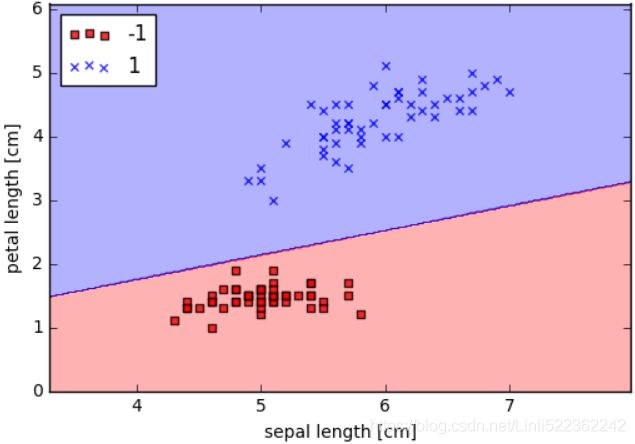
plot_decision_regions(X, y, classifier=ppn)
plt.xlabel('sepal length [cm]')
plt.ylabel('petal length [cm]')
plt.legend(loc='upper left')
plt.show()After executing the preceding code example, we should now see a plot of the decision regions, as shown in the following figure:
As we can see in the preceding plot, the perceptron learned a decision boundary that was able to classify all flower samples in the Iris training subset perfectly.
Note
Although the perceptron classified the two Iris flower classes perfectly, convergence is one of the biggest problems of the perceptron. Frank Rosenblatt proved mathematically that the perceptron learning rule converges if the two classes can be separated by a linear hyperplane. However, if classes cannot be separated perfectly by such a linear decision boundary, the weights will never stop updating unless we set a maximum number of epochs.
##########################################
Help for understanding
numpy.ravel(array_like):Return a contiguous flattened array.
##########################################
Adaptive linear neurons and the convergence of learning
In this section, we will take a look at another type of single-layer neural network: ADAptive LInear NEuron (Adaline). Adaline was published by Bernard Widrow and his doctoral student Tedd Hoff, only a few years after Frank Rosenblatt's
perceptron algorithm, and can be considered as an improvement on the latter. (Refer to An Adaptive "Adaline" Neuron Using Chemical "Memistors", Technical Report Number 1553-2, B. Widrow and others, Stanford Electron Labs, Stanford, CA, October 1960).
The Adaline algorithm is particularly interesting because it illustrates the key concepts of defining and minimizing continuous cost functions. This lays the groundwork for understanding more advanced machine learning algorithms for
classification, such as logistic regression, support vector machines, and regression models, which we will discuss in future chapters.
The key difference between the Adaline rule (also known as the Widrow-Hoff rule) and Rosenblatt's perceptron is that the weights are updated based on a linear activation function rather than a unit step function like in the perceptron. In Adaline, this linear activation function 
is simply the identity function of the net input so that 
.
Perceptron 
Note: Perceptron will traverse and update the weights of all feature items before entering the next loop(for next instance)
Note: the weight update is calculated based on all samples in the training set
#OR updating the weights based on the sum of the accumulated errors over all samples xi.
While the linear activation function is used for learning the weights, we still use a threshold function to make the final prediction, which is similar to the unit step function that we have seen earlier. The main differences between the perceptron and Adaline algorithm are highlighted in the above figure.
The illustration shows that the Adaline algorithm compares the true class labels with the linear activation function's continuous valued output to compute the model error and update the weights. In contrast, the perceptron compares the true class labels to the predicted class labels.
Minimizing cost functions with gradient descent
One of the key ingredients of supervised machine learning algorithms is to define an objective function that is to be optimized during the learning process. This objective function is often a cost function that we want to minimize. In the case of Adaline, we can define the cost function J to learn the weights as the Sum of Squared Errors (SSE) between the calculated outcomes and the true class labels
The term 
is just added for our convenience; it will make it easier to derive the gradient, as we will see in the following paragraphs. The main advantage of this continuous linear activation function is—in contrast to the unit step function—that the cost function becomes differentiable. Another nice property of this cost function is that it is convex; thus, we can use a simple, yet powerful, optimization algorithm called gradient descent
(https://blog.csdn.net/Linli522362242/article/details/104005906)to find the weights that minimize our cost function to classify the samples in the Iris dataset.
As illustrated in the following figure, we can describe the principle behind gradient descent as climbing down a hill until a local or global cost minimum is reached. In each iteration, we take a step away from the gradient where the step size is determined by the value of the learning rate as well as the slope of the gradient:
Using gradient descent, we can now update the weights by taking a step away from the gradient 
of our cost function J(w) : 
Here, the weight change 
is defined as the negative gradient multiplied by the learning rate 
: 
To compute the gradient of the cost function, we need to compute the partial derivative of the cost function with respect to each weight 
: 
So that we can write the update of weight as: 
Since we update all weights simultaneously, our Adaline learning rule becomes w := w + .
###############################
Note
For those who are familiar with calculus, the partial derivative of the SSE cost function with respect to the jth weight in can be obtained as follows: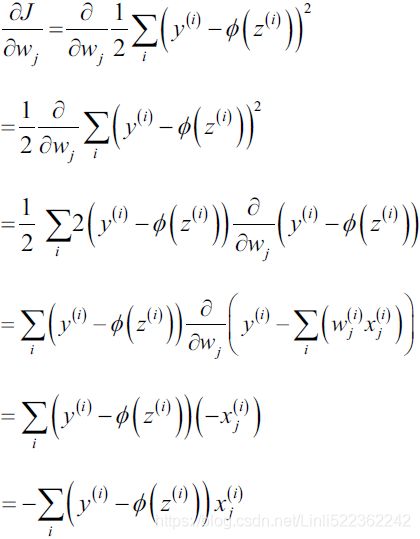
###############################
Although the Adaline learning rule looks identical to the perceptron rule, the 
with 
is a real number and not an integer class label. Furthermore, the weight update is calculated based on all samples in the training set (instead of updating the weights incrementally after each sample), which is why this approach is also referred to as "batch" gradient descent.
Implementing an Adaptive Linear Neuron in Python
Since the perceptron rule and Adaline are very similar, we will take the perceptron implementation that we defined earlier and change the fit method so that the weights are updated by minimizing the cost function via gradient descent:
#updating the weights based on the sum of the accumulated errors over all samples xi.
import pandas as pd
df = pd.read_csv('L:/MachineLearningInAction/machine_learning_databases/iris/iris.data', header=None)
df.head()
import matplotlib.pyplot as plt
import numpy as np
# select setosa and versicolor
y = df.iloc[0:100, 4].values
y = np.where(y=='Iris-setosa', -1, 1)
y
# extract sepal length and peta length
X = df.iloc[0:100, [0,2]].values
X[:5]
import numpy as np
class AdalineGD(object):
#Parameters
# eta: Learning rate (between 0.0 and 1.0)
# n_iter: Passes over the training dataset
# random_state: Random number generator seed for random weight
#Attributes
# w_ : 1d-array # weights after fitting
# cost_ : Sum-of-squares cost function value in each epoch
#random seed
def __init__(self, eta=0.01, n_iter=50, random_state=1):
self.eta = eta
self.n_iter = n_iter
self.random_state = random_state
def net_input(self, X): #intercept
return np.dot(X, self.w_[1:]) + self.w_[0] # X(samples, features) dot w(1+features,1) ==> a single column matrix
def activation(self, X):
#Computer linear activation
return X
def fit(self, X, y): #X_array = [n_samples, n_features]
#y: label =[n_samples]
rgen = np.random.RandomState(self.random_state) #1+ n_features
self.w_ = rgen.normal( loc=0.0, scale=0.01, size=1+X.shape[1] )
self.cost_ = []
for i in range(self.n_iter):
net_input = self.net_input(X) # single column matrix
output = self.activation(net_input) #single column matrix
errors = (y-output) # result_vertical #single column matrix #rows == number of X_samples
#feature_weight
self.w_[1:] += self.eta * X.T.dot(errors) # X.T (n_features, n_samples) #single column matrix#rows==numberOfFeatures
self.w_[0] += self.eta * errors.sum()
cost = (errors **2).sum() /2.0
self.cost_.append(cost)
return self
def predict(self, X):
return np.where( self.activation( self.net_input(X) )>=0.0, 1, -1 ) Instead of updating the weights after evaluating each individual training sample, as in the perceptron, we calculate the gradient based on the whole training dataset via self.eta * errors.sum() for the zero-weight 
and via self.eta * X.T.dot(errors) for the weights 1 to m where X.T.dot(errors) is a matrix-vector multiplication between our feature matrix(shape(features, samples)) and the error vector(shape(samples,1)). Similar to the previous perceptron implementation, we collect the cost values in a list self.cost_ to check if the algorithm converged after training.
######################
Note
Performing a matrix-vector multiplication is similar to calculating a vector dot product where each row in the matrix is treated as a single row vector. This vectorized approach represents a more compact notation and results in a more
efficient computation using NumPy. For example: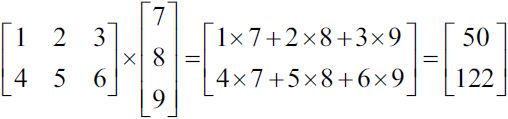
######################
In practice, it often requires some experimentation to find a good learning rate 
for optimal convergence. So, let's choose two different learning rates 
and 
to start with and plot the cost functions versus the number of epochs to see how well the Adaline implementation learns from the training data.
######################
Note
The learning rate (eta), as well as the number of epochs (n_iter), are the so-called hyperparameters of the perceptron and Adaline learning algorithms. In Chapter 6, Learning Best Practices for Model Evaluation and Hyperparameter Tuning, we will take a look at different techniques to automatically find the values of different hyperparameters that yield optimal performance of the classification model.
######################
Let us now plot the cost against the number of epochs for the two different learning rates:
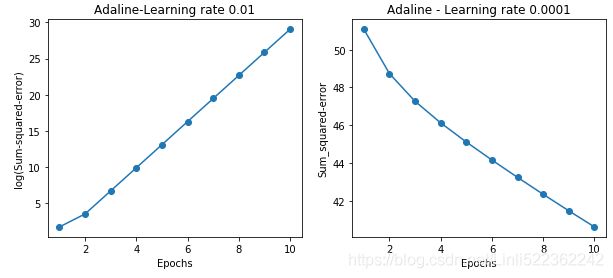
import matplotlib.pyplot as plt
fig, ax = plt.subplots(nrows = 1, ncols =2, figsize=(10,4))
ada1 = AdalineGD(n_iter =10, eta=0.01).fit(X,y)
ax[0].plot( range(1, len(ada1.cost_) +1), np.log10(ada1.cost_), marker='o' )
ax[0].set_xlabel('Epochs')
ax[0].set_ylabel('log(Sum-squared-error)')
ax[0].set_title('Adaline-Learning rate 0.01')
ada2 = AdalineGD(n_iter=10, eta=0.0001).fit(X,y)
ax[1].plot( range(1, len(ada2.cost_) +1), ada2.cost_, marker='o')
ax[1].set_xlabel('Epochs')
ax[1].set_ylabel('Sum_squared-error')
ax[1].set_title('Adaline - Learning rate 0.0001')
plt.show() 
As we can see in the resulting cost-function plots, we encountered two different types of problem. The left chart shows what could happen if we choose a learning rate that is too large. Instead of minimizing the cost function, the error becomes larger in every epoch, because we 超过overshoot the global minimum. On the other hand, we can see that the cost decreases on the right plot, but the chosen learning rate
is so small that the algorithm would require a very large number of epochs to converge to the global cost minimum.
The following figure illustrates what might happen if we change the value of a particular weight parameter to minimize the cost function J. The left subfigure illustrates the case of a well-chosen learning rate, where the cost decreases gradually, moving in the direction of the global minimum. The subfigure on the right, however, illustrates what happens if we choose a learning rate that is too large—we overshoot the global minimum:
Improving gradient descent through feature scaling
Many machine learning algorithms that we will encounter require some sort of feature scaling for optimal performance, which we will discuss in more detail in (A Tour of Machine Learning Classifiers Using Scikit-learn)
https://blog.csdn.net/Linli522362242/article/details/96480059. Gradient descent is one of the many algorithms that benefit from feature scaling. Here, we will use a feature scaling method called standardization, which gives our
data the property of a standard normal distribution. The mean of each feature is centered at value 0 and the feature column has a standard deviation of 1. For example, to standardize the j th feature, we simply need to subtract the sample mean 
from every training sample and divide it by its standard deviation 
:
Here 
is a vector consisting of the j th feature values of all training samples n . and this standardization technique is applied to each feature j in our dataset.
One of the reasons why standardization helps with gradient descent learning is that the optimizer has to go through fewer steps to find a good or optimal solution (the global cost minimum), as illustrated in the following figure, where the subfigures represent the cost surface as a function of two model weights in a two-dimensional classification problem:
Standardization can easily be achieved using the built-in NumPy methods mean and std:
X_std = np.copy(X)
X_std[:,0] = (X[:,0] - X[:,0].mean()) / X[:,0].std()
X_std[:,1] = (X[:,1] - X[:,1].mean()) / X[:,1].std()
X_std[:5]
ada = AdalineGD(n_iter=15, eta=0.01)
ada.fit(X_std, y)
plt.figure( figsize=(20,6) )
plt.subplot(121)
plot_decision_regions(X_std, y, classifier=ada)
plt.title('Adaline - Gradient Descent', fontsize=15)
plt.xlabel('sepal length [standardized]', fontsize=15)
plt.ylabel('petal length [standardized]', fontsize=15)
plt.legend(loc='upper left', fontsize=15)
plt.tight_layout()
plt.subplot(122)
plt.plot(range(1,len(ada.cost_) +1), ada.cost_, marker='o')
plt.xlabel('Epochs', fontsize=15)
plt.ylabel('Sum-squared-error', fontsize=15)
plt.subplots_adjust(wspace=0.08)
plt.show()
As we can see in the plots, Adaline has now converged after training on the standardized features using a learning rate 
=0.01 . However, note that the SSE remains non-zero even though all samples were classified correctly.
Large-scale machine learning and stochastic gradient descent
In the previous section, we learned how to minimize a cost function by taking a step in the opposite direction of a cost gradient that is calculated from the whole training set; this is why this approach is sometimes also referred to as batch gradient descent. Now imagine we have a very large dataset with millions of data points, which is not uncommon in many machine learning applications. Running batch gradient descent can be computationally quite costly in such scenarios since we need to reevaluate the whole training dataset each time we take one step towards the global minimum.
A popular alternative to the batch gradient descent algorithm is stochastic gradient descent, sometimes also called iterative or on-line gradient descent. Instead of updating the weights based on the sum of the accumulated errors over all samples 
:
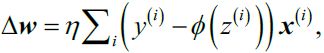
We update the weights incrementally for each training sample:
Although stochastic gradient descent can be considered as an approximation of gradient descent, it typically reaches convergence much faster because of the more frequent weight updates. Since each gradient is calculated based on a single training example, the error surface is noisier than in gradient descent, which can also have the advantage that stochastic gradient descent can escape shallow local minima more readily if we are working with nonlinear cost functions, as we will see later in Chapter 12, Implementing a Multilayer Artificial Neural Network from Scratch. To obtain satisfying results via stochastic gradient descent, it is important to present it training data in a random order; also, we want to shuffle the training set for every epoch to prevent cycles.
#################################
Note
In stochastic gradient descent implementations, the fixed learning rate 
is often replaced by an adaptive learning rate that decreases over time, for example, 
where 
and 
are constants. Note that stochastic gradient descent does not reach the global minimum but an area very close to it. By using an adaptive learning rate, we can achieve further annealing磨炼 to a better global minimum
#################################
Another advantage of stochastic gradient descent is that we can use it for online learning. In online learning, our model is trained on-the-fly as new training data arrives. This is especially useful if we are accumulating large amounts of data—for example, customer data in typical web applications. Using online learning, the system can immediately adapt to changes and the training data can be discarded after updating the model if storage space in an issue.
#################################
Note
A compromise between batch gradient descent and stochastic gradient descent is socalled mini-batch learning. Mini-batch learning can be understood as applying batch gradient descent to smaller subsets of the training data, for example, 32 samples at a time. The advantage over batch gradient descent is that convergence is reached faster via mini-batches because of the more frequent weight updates. Furthermore, mini-batch learning allows us to replace the for loop over the training samples in stochastic gradient descent with vectorized operations, which can further improve the computational efficiency of our learning algorithm.
#################################
Since we already implemented the Adaline learning rule using gradient descent, we only need to make a few adjustments to modify the learning algorithm to update the weights via stochastic gradient descent. Inside the fit method, we will now update the weights after each training sample. Furthermore, we will implement an additional
partial_fit method, which does not reinitialize the weights, for online learning. In order to check whether our algorithm converged after training, we will calculate the cost as the average cost of the training samples in each epoch. Furthermore, we will add an option to shuffle the training data before each epoch to avoid repetitive cycles
when we are optimizing the cost function; via the random_state parameter, we allow the specification of a random seed for reproducibility:
class AdalineSGD(object):
#Parameters
# eta: Learning rate (between 0.0 and 1.0)
# n_iter: Passes over the training dataset
# shuffle : bool (default: True) Shuffles training data every epoch if True to prevent cycles.
# random_state: Random number generator seed for random weight
#Attributes
# w_ : 1d-array # weights after fitting
# cost_ : Sum-of-squares cost function value in each epoch
#random seed
def __init__(self, eta=0.01, n_iter=10, shuffle=True, random_state=None):
self.eta = eta
self.n_iter = n_iter
self.w_initialized = False#############
self.shuffle = shuffle#############
self.random_state=random_state
def _initialize_weights(self, m):
self.rgen = np.random.RandomState(self.random_state)
self.w_ = self.rgen.normal(loc=0.0, scale=0.01, size=1+m) #numOfFeatures + 1
self.w_initialized = True
def activation(self, X):
return X
def net_input(self, X):
return np.dot(X, self.w_[1:]) + self.w_[0]
def _shuffle(self, X,y):
r=self.rgen.permutation(len(y)) #shuffle
return X[r], y[r] #selection or pick in order(r)
def _update_weights(self, xi, target):
# Apply Adaline learning rule to update the weights
output = self.activation( self.net_input(xi) )
error = (target - output)
# VS self.w_[1:] += self.eta * X.T.dot(errors) # X.T (n_features, n_samples)
self.w_[1:] += self.eta * xi.dot(error) #update the weights for each sample
self.w_[0] += self.eta * error
cost = 0.5 * error**2
return cost
def fit(self, X, y): # X : {array-like}, shape = [n_samples, n_features]
self._initialize_weights(X.shape[1])
self.cost_ = []
for i in range(self.n_iter):
if self.shuffle:
X, y = self._shuffle(X,y)
cost = []
for xi, target in zip(X,y):
cost.append(self._update_weights(xi, target)) #append all costs
avg_cost = sum(cost) / len(y)
self.cost_.append(avg_cost)
return self
def partial_fit(self, X, y):
if not self.w_initialized: #has not reinitialize the weights
self._initialize_weights(X.shape[1])
if y.ravel().shape[0] > 1:
for xi, target in zip(X,y):
self._update_weights(xi, target)
else:
self._update_weights(X,y)
return self
def predict(self, X):
return np.where(self.activation(self.net_input(X))>=0.0, 1, -1)The _shuffle method that we are now using in the AdalineSGD classifier works as follows: via the permutation function in np.random, we generate a random sequence of unique numbers in the range 0 to 100. Those numbers can then be used as indices to shuffle our feature matrix and class label vector.
We can then use the fit method to train the AdalineSGD classifier and use our plot_decision_regions to plot our training results:
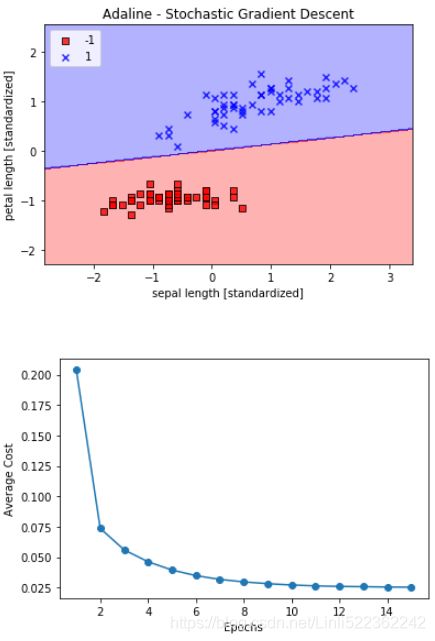
ada = AdalineSGD(n_iter=15, eta=0.01, random_state=1)
ada.fit(X_std, y)
plot_decision_regions(X_std, y, classifier=ada)
plt.title('Adaline - Stochastic Gradient Descent')
plt.xlabel('sepal length [standardized]')
plt.ylabel('petal length [standardized]')
plt.legend(loc='upper left')
plt.show()
plt.plot(range(1, len(ada.cost_)+1), ada.cost_, marker='o')
plt.xlabel('Epochs')
plt.ylabel('Average Cost')
plt.show()The two plots that we obtain from executing the preceding code example are shown in the following figure:
As we can see, the average cost goes down pretty quickly, and the final decision boundary after 15 epochs looks similar to the batch gradient descent Adaline. If we want to update our model, for example, in an online learning scenario with streaming data, we could simply call the partial_fit method on individual samples—for instance ada.partial_fit(X_std[0, :], y[0]).
Summary
we gained a good understanding of the basic concepts of linear classifiers for supervised learning. After we implemented a perceptron, we saw how we can train adaptive linear neurons efficiently via a vectorized implementation of gradient descent and online learning via stochastic gradient descent.
Now that we have seen how to implement simple classifiers in Python, we are ready to move on to the https://blog.csdn.net/Linli522362242/article/details/96480059, where we will use the Python scikit-learn machine
learning library to get access to more advanced and powerful machine learning classifiers that are commonly used in academia as well as in industry. The objectoriented approach that we used to implement the perceptron and Adaline algorithms will help with understanding the scikit-learn API, which is implemented based on the same core concepts that we used in this chapter: the fit and predict methods. Based on these core concepts, we will learn about logistic regression for modeling class probabilities and support vector machines for working with nonlinear decision boundaries. In addition, we will introduce a different class of supervised learning algorithms, tree-based algorithms, which are commonly combined into robust ensemble classifiers.