算法笔记学习(4)---邻接矩阵、邻接表、拓扑排序
邻接矩阵
设图G(V,E)的顶点标号为0, 1,…,N-1,那么可以令二维数组G[N] [N]的两维分别表示图的顶点标号,即如果G[ i ] [ j ]为1,则说明顶点i和顶点j之间有边;如果G[i] [j]]为0,则说明顶点i和顶点j之间不存在边,而这个二维数组G[ ] [ ]则被称为邻接矩阵。另外,如果存在边权,则可以令G[ i ] [ j ]存放边权,对不存在的边可以设边权为0、-1或是一个很大的数。
图10-4是一个作为举例的无向图以及对应的邻接矩阵(边权为0表示不存在边),显然对无向图来说,邻接矩阵是一个对称矩阵。
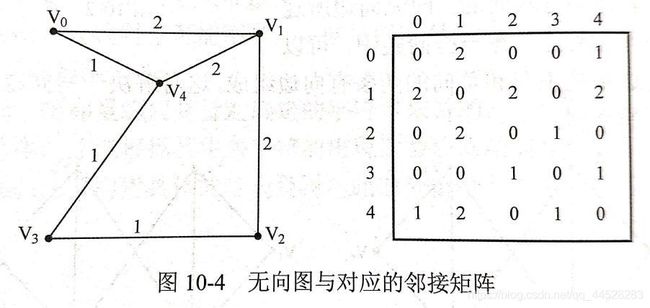
虽然邻接矩阵比较好写,但是由于需要开一个二维数组,如果顶点数目太大,便可能会超过题目限制的内存。因此邻接矩阵只适用于顶点数目不太大(一般不超过1000)的题目。
邻接表
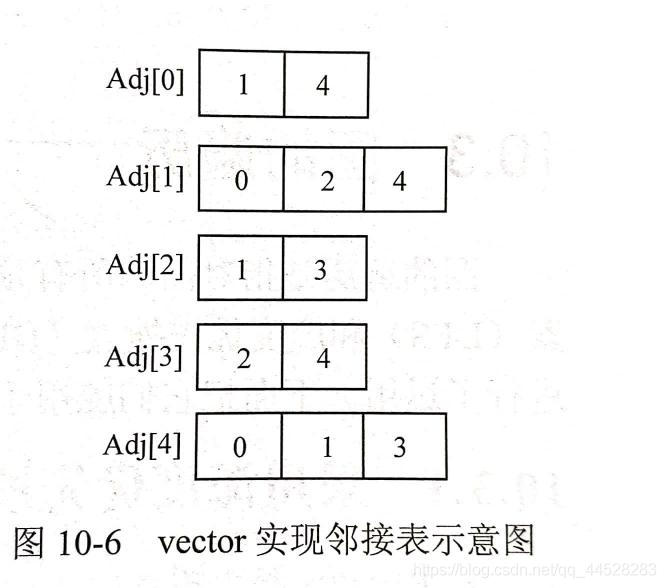
设图G(V,E)的顶点编号为0,1,…,N-1,每个顶点都可能有若干条出边,如果把同一个顶点的所有出边放在一个列表中,那么N个项点就会有N个列表(没有出边,则对应空表)。这N个列表被称为图G的邻接表,记为Adj[N], 其中Adj[i]存放顶点i的所有出边组成的列表,这样Adj[0], Adj[1],…, Adj[N-1]就分别都是一个列表。由于列表可以用链表实现,如果画出图10-4对应的邻接表,就会得到图10-5。其中Adj[0]用链表连接了两个结点,每个结点存放一条边的信息(括号外的数字是边的终点编号,括号内的数字是边权),于是0号顶点有两条出边:一条的终点为1号顶点(边权为2);另一条边的终点为4号顶点(边权为1)。而对Adj[4]来说,它表示4号顶点的三条出边的信息,这三条出边的终点分别是0号顶点、1号顶点、3号顶点,边权分别为1、2、1。

对初学者来说,可能会不太容易很快就熟练使用链表来实现邻接表,因此此处介绍另一种更为简单的工具来实现邻接表: vector ,它能让初学者更快上手并易于使用,且不易出错。
由于vector有变长数组之称,因此可以开个vector 数组Adj[N],其中N为顶点个数。这样每个Adj[i]就都是一个变长数组vector,使得存储空间只与图的边数有关。
如果邻接表只存放每条边的终点编号,而不存放边权,则vector中的元素类型可以直接定义为int型,如下所示:
vector<int> Adj[N];
图10-6为把图10-5中的邻接表采用vector 数组进行存储的情况(只存放边的终点编号)。
如果想添加一条从1号顶点到达3号顶点的有向边,只需要在Adj[1]中添加终点编号3即可,代码如下所示(如果是无向边,就再添加一条从3号顶点到达1号顶点的有向边):
Adj[1].push_back(3);
如果需要同时存放边的终点编号和边权,那么可以建立结构体Node,用来存放每条边的终点编号和边权,代码如下所示:
struct Node{
int v;//边的终点编号
int w;//边权
};
这样vector邻接表中的元素类型就是Node型的,如下所示:
vector<Node> Adj[N];
此时如果想要添加从1号到达3号顶点的有向边,边权为4,就可以定义一个Node型的临时变量temp,令temp.v=3、temp.w=4,然后把temp加入到Adj[1]中即可,代码如下所示:
Node temp;
temp.v = 3;
temp.w = 4;
Adj[1].push_back(temp);
当然,更快的做法是定义结构体Node的构造函数,代码如下所示:
struct Node{
int v,w;
Node(int _v ,int _w) : (v)_v , w(_w) {
}//构造函数,注意没有分号
};
这样就能不定义临时变量来实现加边操作,代码如下所示:
Adj[1].push_back(Node(3,4));
于是就可以使用vector来很方便地实现邻接表,在一些**顶点数目较大**(一般顶点个数在1000以上)的情况下,一般都需要使用邻接表而非邻接矩阵来存储图。
拓扑排序
如果一个有向图的任意项点都无法通过一些有向边回到自身, 那么称这个有向图为有向无环图(Directed Acyclic Graph, DAG)。 图10-56给出了几个DAG的例子。
拓扑排序是将有向无环图G的所有项点排成一个线性序列,使得对图G中的任意两个项点u、V,如果存在边u->V,那么在序列中u一定在V 前面。这个序列又被称为拓扑序列。
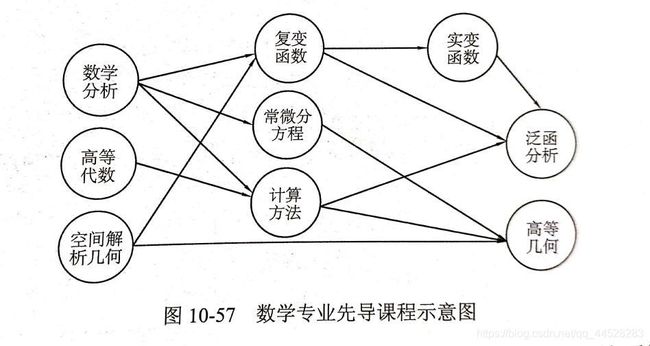
以图10-57 数学专业的某几门课程的学习先后顺序为例(为了方便阅读,图中省略了一部分关系),可以获知,“数学分析”是“复变函数"、“常微分方程”、“计算方法"的先导课程,“复变函数”是“实变函数”和“泛函分析”的先导课程,“实变函数”又是“泛函分析”的先导课程,等等。显然,对一门课来说,必须要先学习它的先导课程才能很好地学习这门课,而且先导课程之间不能够形成环(例如如果“泛函分析”同时又是“空间解析几何”的先导课程,就乱套了)。
同时还会发现,如果两门课程之间没有直接或间接的先导关系,那么这两门学习的先后顺序是任意的(例如“复变函数”与“计算方法"的学习顺序就是任意的)。于是可以把上面的课程排成一个学习的先后序列,使得这个序列中的课程顺序满足图10-57的先导课程顺序,如图10-58所示。
这样读者应当能理解什么是拓扑排序了,下面讲解求解拓扑序列的方法。通过上面的例子会发现,如果某一门课没有先导课程或是所有先导课程都已经学习完毕,那么这门课就可以学习了。如果有多门这样的课,它们的学习顺序任意。对应到图中,这个做法可以抽象为以下步骤:
①定义一个队列Q,并把所有入度为0的结点加入队列。
②取队首结点,输出。然后删去所有从它出发的边,并令这些边到达的项点的入度减1,如果某个顶点的入度减为0,则将其加入队列。
③反复进行②操作,直到队列为空。如果队列为空时入过队的结点数目恰好为N,说明拓扑排序成功,图G为有向无环图;否则,拓扑排序失败,图G中有环。
可使用邻接表实现拓扑排序。显然,由于需要记录结点的入度,因此需要额外建立一个数组inDegree[MAXV],并在程序一开始读入图时就记录好每个结点的入度。接下来就只需要按上面所说的步骤进行实现即可,拓扑排序的代码如下:
vector<int> G[MAXV];//邻接表
int n, m, inDegree[MAXV];//顶点数、入度
//拓扑排序
bool topologicalSort()
{
int num = 0;//记录加入拓扑序列的顶点数
queue<int> q;
for(int i=0;i<n;i++)
{
if(inDegree[i]==0)
{
q.push(i);//将所有入度为0的顶点入队
}
}
while(!q.empty())
{
int u = q.front();//取队首顶点
//printf("%d",u);//此处可输出顶点u,作为拓扑序列中的顶点
q.pop();
for(int i=0;i<G[u].size();i++)
{
int v = G[u][i];//u的后继节点v
inDegree[v]--;//顶点v的入度减1
if(inDegree[v]==0) //顶点v的入度减为0则入队
{
q.push(v);
}
}
G[u].clear();//清空顶点u的所有出边(如无必要可不写)
num++;
}
if(num == n) return true; //加入拓扑序列的顶点数为n,说明拓扑排序成功
else return false; //加入拓扑序列的顶点数小于n,说明拓扑排序失败
}
拓扑排序的很重要的应用就是判断一个给定的图是否是有向无环图。正如上面的代码,如果topologicalSort()函数返回true,则说明拓扑排序成功,给定的图是有向无环图;否则,说明拓扑排序失败,给定的图中有环。
最后指出,如果要求有多个入度为0的项点,选择编号最小的顶点,那么把queue改成priority_ queue, 并保持队首元素(堆项元素)是优先队列中最小的元素即可(当然用set也是可以的)。
实例:CCFCSP认证 202009-3 点亮数字人生
题目详情->点亮数字人生
用拓扑排序实现,代码如下:
#include