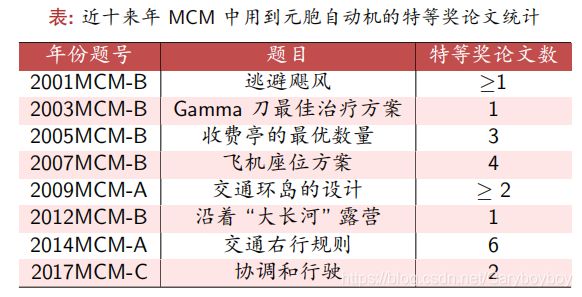
元胞自动机
元胞自动机
Gary哥哥的哥哥 2021.1.29
Background:
- 最初的元胞自动机是由冯 · 诺依曼在 1950 年代为模拟生物细胞的自我复制而提出的. 但是并未受到学术界重视.
- 1970 年, 剑桥大学的约翰 · 何顿 · 康威设计了一个电脑游戏“生命游戏” 后, 元胞自动机才吸引了科学家们的注意.
- 1983 年 S.Wolfram 发表了一系列论文. 对初等元胞机 256 种规则所产生的模型进行了深入研究, 并用熵来描述其演化行为, 将细胞自动机分为平稳型, 周期型, 混沌型和复杂型.
应用
-
社会学: 元胞自动机经常用于研究个人行为的社会性, 流行现象. 例如人口迁移, 公共场所内人员的疏散, 流行病传播.
-
图形学: 元胞自动机以其特有的结构的简单性, 内在的并行性以及复杂计算的能力成为密码学中研究的热点方向一.
-
物理学: 在物理学中, 元胞自动机已成功的应用于流体, 磁 场, 电场, 热传导等的模拟. 例如格子气自动机.
在实际比赛中的应用
可见在解决交通问题上面有着广泛的应用,我们稍后会讲解为什么?
相关定义
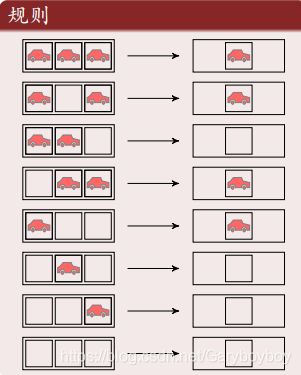
交通规则
- 元胞分布于一维线性网格上.
- 元胞仅具有车和空两种状态.
- 元胞状态由周围两邻居决定.
生命游戏
这是一个元胞自动机发展历史上著名的数学问题
- 元胞分布于二维方型网格上.
- 元胞仅具有生和死两种状态.
- 元胞状态由周围八邻居决定.
具体定义
- 离散的系统: 元胞是定义在有限的时间和空间上的, 并且元胞的状态是有限.
- ==动力学系统==: 元胞自动机的举止行为具有动力学特征.
- 简单与复杂: 元胞自动机用简单规则控制相互作用的元胞模拟复杂世界.
构成要素
-
元胞
- 状态: 每一个元胞都有记忆贮存状态的功能.
- 离散: 简单情况下, 元胞只有两种可能状态; 较复杂情况下, 元胞具有多种状态.
- 更新: 元胞的状态都安照动力规则不断更新.
-
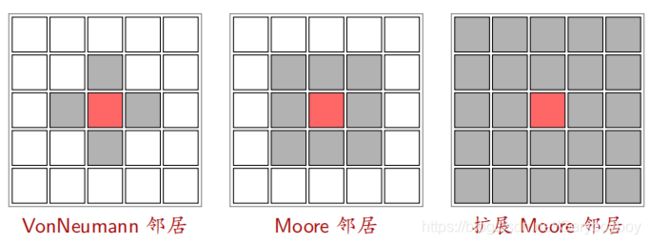
邻居
-
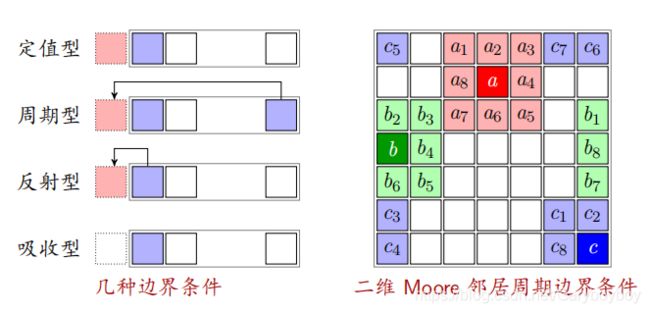
边界
实际问题中需要考虑边界
-
规则
实际上就是 状态转移函数
- 总和型:周围邻居状态和决定
- 合法型:局部的影响性
森林火灾案例
程序实现
% simulate forest fire with cellular automata
% zhou lvwen: [email protected]
% August 15 2010
n = 300;
Plight = 5e-6;
Pgrowth = 1e-2;
UL = [n 1:n-1]; % 左邻居
DR = [2:n 1]; %右邻居
veg=zeros(n,n);
% C = cat(dim, A, B) 沿 dim 指定的数组维度串联数组 A 和 B。dim 参数必须是正整数值。
imh = image(cat(3,veg,veg,veg));%veg分别为红绿蓝色
% veg = empty=0 burning=1 green=2
for i=1:3000
%nearby fires? 四个邻居加起来看更加直观
sum = (veg(UL,:)==1) + ...
(veg(:,UL)==1) + (veg(:,DR)==1) + ...
(veg(DR,:)==1);
% Tree=Tree-burning+new
veg = 2*(veg==2) - ...
( (veg==2) & (sum>0 | (rand(n,n)交通问题
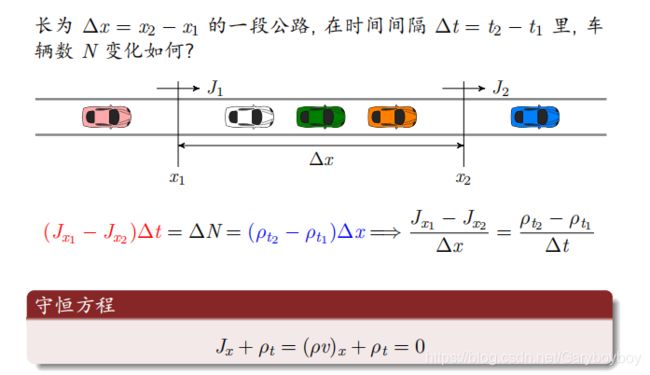
车距与密度
- 流量方程:
- J=ρv
守恒方程
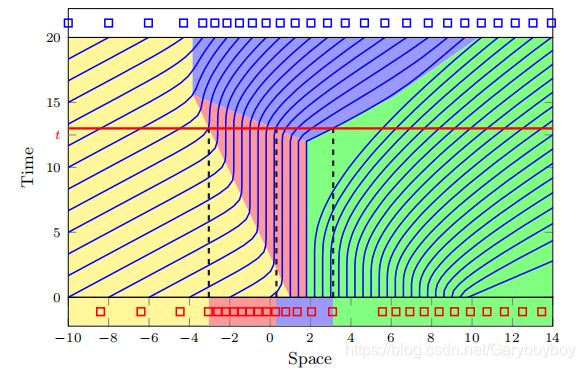
时空轨迹
宏观连续型模型
交通案例分析
理论分析
单车道
function [rho, flux, vmean] = ns(rho, p, L, tmax, animation, spacetime)
%
% NS: This script implements the Nagel Schreckenberg cellular automata based
% traffic model. Car move forward governed by NS algorithm:
%
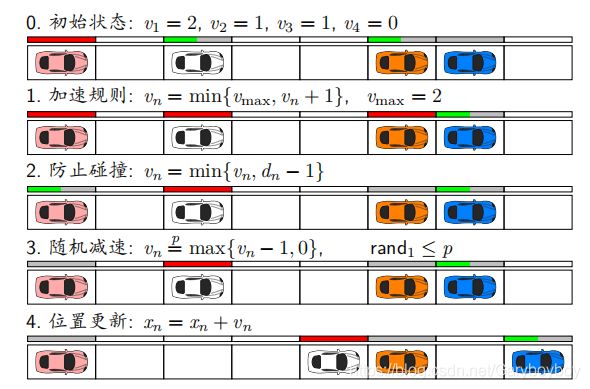
% 1. Acceleration. If the vehicle can speed up without hitting the speed
% limit vmax it will add one to its velocity, vn 鈫? vn + 1. Otherwise,
% the vehicle has constant speed, vn 鈫? vn.
%
% 2. Collision prevention. If the distance between the vehicle and the car
% ahead of it, dn, is less than or equal to vn , i.e. the nth vehicle
% will collide if it doesn't slow down, then vn 鈫? dn 鈭? 1.
%
% 3. Random slowing. Vehicles often slow for non-traffic reasons (cell
% phones, coffee mugs, even laptops) and drivers occasionally make
% irrational choices. With some probability pbrake, vn 鈫? vn 鈭? 1,
% presuming vn > 0.
%
% 4. Vehicle movement. The vehicles are deterministically moved by their
% velocities, xn 鈫? xn + vn .
%
% USAGE: flux = ns(rho, p, L, tmax, isdraw)
% rho = density of the traffic
% p = probability of random braking
% L = length of the load
% tmax = number of the iterations
% animation = if show the animation of the traffic
% spacetime = if plot the space-time after the simuation ended.
% flux = flux of the traffic
%
% zhou lvwen: zhou.lv.wen@gmail.com
%
if nargin == 0;
rho = 0.25; p = 0.25; L = 100; tmax = 100;
animation = true; spacetime = true;
end
vmax = 5; % maximun speed
% place a distribution with density
ncar = round(L*rho); %车的数量
rho = ncar/L;
x = sort(randsample(1:L, ncar)); %每个车子的位置
v = vmax * ones(1,ncar); % start everyone initially at vmax,每个车子的速度
if animation; h = plotcirc(L,x,0.1); end
flux = 0; % number of cars that pass through the end
vmean = 0;
road = zeros(tmax, L);
for t = 1:tmax
% acceleration
v = min(v+1, vmax);
%collision prevention
gaps = gaplength(x,L); % determine the space vehicles have to move,车头到车头
v = min(v, gaps-1);%车头到前车尾
% random speed drops
vdrops = ( rand(1,ncar)<p );
v = max(v-vdrops,0);
% update the position
x = x + v;
passed = x>L; % cars passed at time r
x(passed) = x(passed) - L;% periodic boundary conditions
if t>tmax/2
flux = flux + sum(v/L); %flux = flux + sum(passed);
vmean = vmean + mean(v);
end
road(t,x) = 1;
if animation; h = plotcirc(L,x,0.1,h); end
end
flux = flux/(tmax/2);
vmean = vmean/(tmax/2);
if spacetime; figure;imagesc(road);colormap([1,1,1;0,0,0]);axis image; end
% -------------------------------------------------------------------------
function gaps = gaplength(x,L)
%
% GAPLENGTH: determine the gaps between vehicles
%
ncar = length(x);
gaps=zeros(1, ncar);
if ncar>0
gaps = x([2:end 1]) -x;
gaps(gaps<=0) = gaps(gaps<=0)+L;
end
% -------------------------------------------------------------------------
function h = plotcirc(L,x,dt,h)
W = 0.05; R = 1;
ncar = length(x);
theta = [0 : 2*pi/L : 2*pi];
xc = cos(theta); yc = sin(theta);
xinner = (R-W/2)*xc; yinner = (R-W/2)*yc;
xouter = (R+W/2)*xc; youter = (R+W/2)*yc;
xi = [xinner(x); xinner(x+1); xouter(x+1); xouter(x)];
yi = [yinner(x); yinner(x+1); youter(x+1); youter(x)];
if nargin == 3
color = randperm(ncar);
h = fill(xi,yi, color); hold on
plot(xinner,yinner, 'k', xouter,youter, 'k','linewidth',1.5)
plot([xinner; xouter], [yinner; youter],'k','linewidth',1.5)
axis image; axis((R+2*W)*[-1 1 -1 1]); axis off
else
for i=1:ncar; set(h(i),'xdata',xi(:,i),'ydata',yi(:,i)); end
end
pause(dt)
多车道
function [rho, flux, vmean] = ns(rho, p, L, tmax, animation, spacetime)
%
% NS: This script implements the Nagel Schreckenberg cellular automata based
% traffic model. Car move forward governed by NS algorithm:
%
% 1. Acceleration. If the vehicle can speed up without hitting the speed
% limit vmax it will add one to its velocity, vn -> vn + 1. Otherwise,
% the vehicle has constant speed, vn -> vn.
%
% 2. Collision prevention. If the distance between the vehicle and the car
% ahead of it, dn, is less than or equal to vn , i.e. the nth vehicle
% will collide if it doesn't slow down, then vn -> dn 鈭� 1.
%
% 3. Random slowing. Vehicles often slow for non-traffic reasons (cell
% phones, coffee mugs, even laptops) and drivers occasionally make
% irrational choices. With some probability pbrake, vn -> vn 鈭� 1,
% presuming vn > 0.
%
% 4. Vehicle movement. The vehicles are deterministically moved by their
% velocities, xn -> xn + vn .
%
% USAGE: flux = ns(rho, p, L, tmax, isdraw)
% rho = density of the traffic
% p = probability of random braking
% L = length of the load
% tmax = number of the iterations
% animation = if show the animation of the traffic
% spacetime = if plot the space-time after the simuation ended.
% flux = flux of the traffic
%
% zhou lvwen: zhou.lv.wen@gmail.com
%
if nargin == 0;
rho = 0.15; p = 0.25; L = 100; tmax = 5000; pchange = 0.5;
animation = 'circle';
end
%rand('seed',1)
vmax = 5; % maximun speed
% place a distribution with density
ncar = round(L*2*rho);
rho = ncar/2/L;
xy = randperm(2*L,ncar);
[y,x] = ind2sub([2, L], xy); % y: 2 for right, 1 for left
v = vmax * ones(1,ncar); % start everyone initially at vmax
switch animation
case 'circle'; h = plotcirc(L,x,y,2);
case 'line'; h = plotline(L,x,y,2);
end
flux = [0 0]; % number of cars that pass through the end
vmean = [0 0];
voffset = 1;
vback = 1;
XY = [x y];
for t = 1:tmax
% determine the space vehicles have to move
[gaps, gapfront, gapback] = gaplength(x,y,L);
% left to right & right to left
l2r = find(y==1 & gaps>vmax+voffset & gapfront>vmax+voffset & gapback>=vback);
r2l = find(y==2 & gaps<vmax & gapfront>gaps & gapback>=vback & rand(size(y))<pchange);
y(l2r) = 2;
y(r2l) = 1;
% acceleration
v = min(v+1, vmax);
gaps = gaplength(x,y,L);
%collision prevention
v = min(v, gaps-1);
% random speed drops
vdrops = ( rand(1,ncar)<p );
v = max(v-vdrops,0);
% update the position
x = x + v;
passed = x>L; % cars passed at time r
x(passed) = x(passed) - L;% periodic boundary conditions
if t>tmax/2
flux(1) = flux(1) + sum(v(y==1)/L); %flux = flux + sum(passed);
flux(2) = flux(2) + sum(v(y==2)/L); %flux = flux + sum(passed);
vmean(1) = vmean(1) + mean(v(y==1));
vmean(2) = vmean(2) + mean(v(y==2));
end
switch animation
case 'circle'; plotcirc(L,x,y,0.1,h);
case 'line'; plotline(L,x,y,0.1,h);
end
end
flux = flux/(tmax/2);
vmean = vmean/(tmax/2);
% -------------------------------------------------------------------------
function [gap, gapfront, gapback] = gaplength(x,y,L)
%
% GAPLENGTH: determine the gaps between vehicles
%
ncar = length(x);
gap = inf*ones(1, ncar);
gapfront = inf*ones(1, ncar);
gapback = inf*ones(1, ncar);
index = 1:ncar;
for i = index
j1 = index(index~=i & y==y(i));
if ~isempty(j1)
d1 = x(j1) - x(i);
d1(d1<-L/2) = d1(d1<-L/2) + L;
if any(d1>0)
gap(i) = min(d1(d1>0));
end
end
j2 = index(index~=i & y~=y(i));
if ~isempty(j2)
d2 = x(j2) - x(i);
d2(d2<-L/2) = d2(d2<-L/2) + L;
if any(d2>=0)
gapfront(i) = min(d2(d2>=0));
end
d3 = x(i) - x(j2);
d3(d3<-L/2) = d3(d3<-L/2) + L;
if any(d3>=0)
gapback(i) = min(d3(d3>=0));
end
end
end
% -------------------------------------------------------------------------
function h = plotcirc(L,x,y,dt,h)
W = 0.05;
ncar = length(x);
theta = [(0-pi/L) : 2*pi/L : (2*pi+pi/L)];
R = ones(size(theta));
theta = [ theta; theta];
R = [R; R+W];
xc = cos(theta); yc = sin(theta);
xinner = (R-W/2).*xc; yinner = (R-W/2).*yc;
xouter = (R+W/2).*xc; youter = (R+W/2).*yc;
i = sub2ind(size(R),y,x);
if nargin == 4
color = randperm(ncar);
xi = [xinner(i); xinner(i+2); xouter(i+2); xouter(i)];
yi = [yinner(i); yinner(i+2); youter(i+2); youter(i)];
h = fill(xi,yi, color); hold on
plot(xinner(1,:),yinner(1,:), 'k', ...
xouter(1,:),youter(1,:), 'k', ...
xouter(2,:),youter(2,:), 'k','linewidth',1.5);
plot([xinner; xouter], [yinner; youter],'k','linewidth',1.5);
axis image;
else
xi = [xinner(i); xinner(i+2); xouter(i+2); xouter(i)];
yi = [yinner(i); yinner(i+2); youter(i+2); youter(i)];
for i=1:ncar; set(h(i),'xdata',xi(:,i),'ydata',yi(:,i)); end
end
pause(dt)
% -------------------------------------------------------------------------
function h = plotline(L,x,y,dt,h)
W = 2;
rmin = 1;
dw = 0.05;
rmax = rmin + dw*(W-1);
ncar = length(x);
ti = 0 : 2*pi/L : 2*pi;
ri = rmin:dw:rmax;
[theta, R] = meshgrid(ti, ri);
xmin = (R-dw/2).*cos(theta);
ymin = (R-dw/2).*sin(theta);
xmax = (R+dw/2).*cos(theta);
ymax = (R+dw/2).*sin(theta);
i = sub2ind(size(R),y,x);
xi = [xmin(i); xmin(i+W); xmax(i+W); xmax(i)];
yi = [ymin(i); ymin(i+W); ymax(i+W); ymax(i)];
if nargin == 6
color = randperm(ncar);
h = fill(xi,yi, color); hold on
plot([xmin; xmax]', [ymin; ymax]', 'k', 'linewidth', 1.5);
plot([xmin; xmax] , [ymin; ymax] , 'k', 'linewidth', 1.5);
axis image;
else
for i=1:ncar; set(h(i),'xdata',xi(:,i),'ydata',yi(:,i)); end
end
pause(dt)
更复杂的可以模拟整个城市的交通网络和收费站问题
更多案例的代码请见
[数学建模]: https://github.com/Gary-code/Mathematic-Modeling/tree/main/%E4%B8%83%E5%A4%A9%E5%AD%A6%E4%BC%9A%E6%95%B0%E5%AD%A6%E5%BB%BA%E6%A8%A1%E8%AF%BE%E7%A8%8B%E4%BB%A3%E7%A0%81/4.%E5%85%83%E8%83%9E%E8%87%AA%E5%8A%A8%E6%9C%BA ““数学建模””
总结
特点
-
离散的空间, 离散的时间.
-
离散有限的状态.
-
同质的元胞.
-
局部的作用, 同步的计算.
-
元胞自动机比较适合解决具有空间离散特点的动力学问题.
-
根据问题适当改造元胞自动机, 可使应用范围更广.
-
不要在不适当的问题上迁强地使用元胞自动机.