Python编程学习笔记 - 使用Pygal模拟掷骰子

我们将使用Python可视化包Pygal来生成可缩放的矢量图形文件。对于需要在尺寸不同的屏幕上显示的图表，这很有用，因为它们将自动缩放，以适合观看者的屏幕。如果你打算以在线方式使用图表，请考虑使用Pygal来生成它们，这样它们在任何设备上显示都会很美观。

1. 创建Die类

下面的类模拟掷一个骰子：

die.py 代码

from random import randint

class Die():

    def __init__(self, num_sides=6):
        self.num_sides = num_sides

    def roll(self):
        return randint(1, self.num_sides)

方法__init__()接受一个可选参数。创建这个类的实例时，如果没有指定任何实参，面数默认为6；如果指定了实参，这个值将用于设置骰子的面数。骰子是根据面数命名的，6面的骰子名为D6，8面的骰子名为D8，以此类推。

方法roll()使用函数randint()来返回一个1和面数之间的随机数。这个函数可能返回起始值1、终止值num_sides或这两个值之间的任何整数。

2. 掷骰子和分析结果

使用这个类来创建图表前，先来掷D6骰子，将结果打印出来，并检查结果是否合理：

die_visual.py 代码

from die import Die
    
die = Die()

results = []
for roll_num in range(1000):
    result = die.roll()
    results.append(result)

frequencies = []
for value in range(1, die.num_sides+1):
    frequency = results.count(value)
    frequencies.append(frequency)

print(frequencies)

为分析结果，我们创建了空列表frequencies，用于存储每种点出现的次数。我们遍历可能的点数（这里为1~6），计算每种点数在results中出现了多少次，并将这个值附加到列表frequencies的末尾。接下来，我们在可视化之前将这个列表打印出来：
[ 155， 167，168， 170，159，181 ]

结果看起来是合理的：我们看到了6个值 – 掷D6骰子时可能出现的每个点数对应一个；我们还发现，没有任何点数出现的频率比其他点数高很多。

3. 绘制直方图

有了频率列表后，我们就可以绘制一个表示结果的直方图。直方图是一种条形图，指出了各种出现的频率。创建这种直方图的代码如下：

import pygal

from die import Die
    
die = Die()

results = []
for roll_num in range(1000):
    result = die.roll()
    results.append(result)

frequencies = []
for value in range(1, die.num_sides+1):
    frequency = results.count(value)
    frequencies.append(frequency)

hist = pygal.Bar()

hist.title    = "Result of rolling one D6 1000 times."

hist.x_labels = [str(n) for n in range(1, die.num_sides+1) ]
#hist.x_labels = ['1','2','3','4','5','6']

hist.x_title  = "Result"
hist.y_title  = "Frequency of Result"

hist.add('D6', frequencies)
hist.render_to_file('die_visual.svg')

为了创建条形图，我们创建了一个pygal.Bar()实例，并将其存储在hist中。接下来，我们设置hist的属性title（用于标示直方图的字符串），将掷D6骰子 的可能结果用作x轴的标签，并给每个轴都添加了标题。我们使用add()将一系列值添加到图表中（向它传递要给添加的值指定的标签，还有一个列表，其中包含将出现在图表中的值）。最后，我们将这个图表渲染为一个SVG文件，这种文件的扩展名必须为.svg。

要查看生成的直方图，最简单的方式是使用Web浏览器。为此，在任何Web浏览器中新建一个标签页，再在其中打开文件die_visual.svg（它位于die_visual.py所在文件夹中）。你将会看到一个类似于下图的图表：

注意，Pygal让这个图具有交互性：如果你将鼠标指向该图表中的任何条形，将看到与之相关联的数据。在同一个图表中绘制多个数据集时，这项功能显得特别有用。

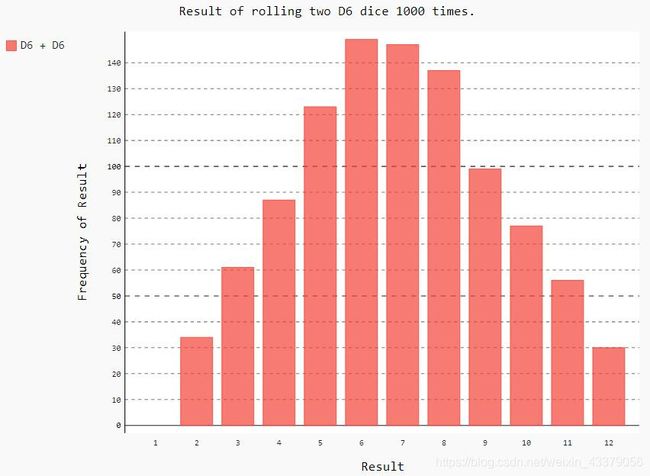
4. 同时掷两个骰子

同时掷两个骰子时，得到的点数更多，结果分布情况也不同。我们修改以前的代码，创建两个D6骰子，以模拟同时掷两个骰子的情况。每次掷两个骰子时，我们都将两个骰子的点数相加，并将结果存储在results中。请复制die_visual.py并将其保存为dice_visual.py，再做如下修改：

import pygal

from die import Die
    
die_1 = Die()
die_2 = Die()

results = []
for roll_num in range(1000):
    result = die_1.roll() + die_2.roll()
    results.append(result)

frequencies = []
max_result = die_1.num_sides + die_2.num_sides
for value in range(1, max_result+1):
    frequency = results.count(value)
    frequencies.append(frequency)

hist = pygal.Bar()

hist.title    = "Result of rolling two D6 dice 1000 times."
hist.x_labels = ['1','2','3','4','5','6','7','8','9','10','11','12']
#hist.x_labels = [ str(i) for i in range(1, 13) ] 
hist.x_title  = "Result"
hist.y_title  = "Frequency of Result"

hist.add('D6 + D6', frequencies)
hist.render_to_file('dice_visual.svg')

下图表显示了掷两个D6骰子时得到的大致结果：

5. 同时掷两个面数不同的骰子

下面来创建一个6面骰子和一个10面骰子，看看同时掷这两个骰子50000次的结果如何？

import pygal

from die import Die

die_1 = Die()
die_2 = Die(10)

results = []
for roll_num in range(50000):
    result = die_1.roll() + die_2.roll()
    results.append(result)

frequencies = []
max_result = die_1.num_sides + die_2.num_sides
for value in range(1, max_result+1):
    frequency = results.count(value)
    frequencies.append(frequency)

hist = pygal.Bar()

hist.title    = "Result of rolling D6 and D10 dice 50000 times."
hist.x_labels = [ str(i) for i in range(1, max_result+1) ] 
hist.x_title  = "Result"
hist.y_title  = "Frequency of Result"

hist.add('D6 + D10', frequencies)
hist.render_to_file('different_dice_visual.svg')

下图显示了最终的图表。可能性最大的点数不是一个，而是5个，这是因为导致出现最小点数和最大点数的组合都只有一种（1和1以及6和10）。

通过使用Pygal来模拟掷骰子的结果，能够非常自由地探索这种现象。只需几分钟，就可以掷各种骰子很多次。

文章内容来自《Python编程 从入门到实践》 [美] Eric Matthes 袁国忠 译