详解Pytorch实现MNIST手写数字识别
目录
1.思路和流程分析
2.准备训练集和测试集
2.1 torchvision.transforms的图形数据处理方法
2.1.1 torchvision.transforms.ToTensor
2.1.2 torchvision.transforms.Normalize(mean, std)
2.1.3 torchvision.transforms.Compose(transforms)
2.2 准备MNIST数据集的Dataset和DataLoader
3.构建模型
3.1 激活函数的使用
3.2 模型中数据的形状(【添加形状变化图形】)
4.模型的训练
5.模型的保存与加载
6.模型的评估
7.完整代码
1.思路和流程分析
流程:
-
准备数据,MNIST数据集可以使用Pytorch API加载,所以不需要自定义dataset类,但是需要准备DataLoader
-
构建模型,这里仅仅使用全连接层堆叠来实现MNIST手写数字识别,如果采用CNN等其他深度网络模型结构,只需要在模型定义那一步做出改变即可
-
训练模型,更新参数
-
模型的保存,保存模型,便于后续的使用
-
模型的评估,使用测试集,观察模型的好坏
2.准备训练集和测试集
调用MNIST返回的结果中图形数据是一个Image对象,需要对其进行处理,对于图像数据的处理,可以采用torchvision.transfroms的方法
2.1 torchvision.transforms的图形数据处理方法
2.1.1 torchvision.transforms.ToTensor
把一个取值范围是[0,255]的PIL.Image或者shape为(H,W,C)的numpy.ndarray,转换成形状为[C,H,W]
其中(H,W,C)意思为(高,宽,通道数),黑白图片的通道数只有1,其中每个像素点的取值为[0,255],彩色图片的通道数为(R,G,B),每个通道的每个像素点的取值为[0,255],三个通道的颜色相互叠加,形成了各种颜色
示例如下:
from torchvision import transforms
import numpy as np
data = np.random.randint(0, 255, size=12)
img = data.reshape(2,2,3)
print(img.shape)
# 注意这种形式,ToTensor方法不能传入参数
img_tensor = transforms.ToTensor()(img) # 转换成tensor
print(img_tensor)
print(img_tensor.shape)输入如下:
shape:(2, 2, 3)
img_tensor:tensor([[[215, 171],
[ 34, 12]],
[[229, 87],
[ 15, 237]],
[[ 10, 55],
[ 72, 204]]], dtype=torch.int32)
new shape:torch.Size([3, 2, 2])2.1.2 torchvision.transforms.Normalize(mean, std)
给定均值:mean,shape和图片的通道数相同(指的是每个通道的均值),方差:std,和图片的通道数相同(指的是每个通道的方差),将会把Tensor规范化处理。
即:Normalized_image=(image-mean)/std
示例如下:
from torchvision import transforms
import numpy as np
import torchvision
data = np.random.randint(0, 255, size=12)
img = data.reshape(2,2,3)
img = transforms.ToTensor()(img) # 转换成tensor
print(img)
print("*"*100)
# 有三个通道就得传入一个长度为3的元组
norm_img = transforms.Normalize((10,10,10), (1,1,1))(img) #进行规范化处理
print(norm_img)输出结果如下:
tensor([[[177, 223],
[ 71, 182]],
[[153, 120],
[173, 33]],
[[162, 233],
[194, 73]]], dtype=torch.int32)
***************************************************************************************
# 167就是(177-10)/1,其余的类似
tensor([[[167, 213],
[ 61, 172]],
[[143, 110],
[163, 23]],
[[152, 223],
[184, 63]]], dtype=torch.int32)注意:在sklearn中,默认上式中的std和mean为数据每列的std和mean,sklearn会在标准化之前算出每一列的std和mean。
但是在api:Normalize中并没有帮我们计算,所以我们需要手动计算
-
当mean为全部数据的均值,std为全部数据的std的时候,才是进行了标准化。
-
如果mean(x)不是全部数据的mean的时候,std(y)也不是的时候,Normalize后的数据分布满足下面的关系:

2.1.3 torchvision.transforms.Compose(transforms)
该方法可以将多个transform组合起来使用。
transforms.Compose([
torchvision.transforms.ToTensor(), #先转化为Tensor
torchvision.transforms.Normalize(mean,std) #在进行正则化
])2.2 准备MNIST数据集的Dataset和DataLoader
# 准备训练集
import torchvision
#准备数据集,其中0.1307,0.3081为MNIST数据的均值和标准差,这样操作能够对其进行标准化
#因为MNIST只有一个通道(黑白图片),所以元组中只有一个值
dataset = torchvision.datasets.MNIST('/data', train=True, download=True,
transform=torchvision.transforms.Compose([
torchvision.transforms.ToTensor(),
torchvision.transforms.Normalize(
(0.1307,), (0.3081,))
]))
#准备数据迭代器
train_dataloader = torch.utils.data.DataLoader(dataset,batch_size=64,shuffle=True)# 准备测试集
import torchvision
#准备数据集,其中0.1307,0.3081为MNIST数据的均值和标准差,这样操作能够对其进行标准化
#因为MNIST只有一个通道(黑白图片),所以元组中只有一个值
dataset = torchvision.datasets.MNIST('/data', train=False, download=True,
transform=torchvision.transforms.Compose([
torchvision.transforms.ToTensor(),
torchvision.transforms.Normalize(
(0.1307,), (0.3081,))
]))
#准备数据迭代器
train_dataloader = torch.utils.data.DataLoader(dataset,batch_size=64,shuffle=True)3.构建模型
补充:全连接层:当前一层的神经元和前一层的神经元相互链接,其核心操作就是,即矩阵的乘法,实现对前一层的数据的变换
模型的构建使用了一个三层的神经网络,其中包括两个全连接层和一个输出层,第一个全连接层会经过激活函数的处理,将处理后的结果交给下一个全连接层,进行变换后输出结果
那么在这个模型中有两个地方需要注意:
-
激活函数如何使用
-
每一层数据的形状
-
模型的损失函数
3.1 激活函数的使用
前面介绍了激活函数的作用,常用的激活函数为Relu激活函数,他的使用非常简单
Relu激活函数由import torch.nn.functional as F提供,F.relu(x)即可对x进行处理
例如:
In [30]: b
Out[30]: tensor([-2, -1, 0, 1, 2])
In [31]: import torch.nn.functional as F
In [32]: F.relu(b)
Out[32]: tensor([0, 0, 0, 1, 2])3.2 模型中数据的形状(【添加形状变化图形】)
-
原始输入数据为的形状:
[batch_size,1,28,28] -
进行形状的修改:
[batch_size,28*28],(全连接层是在进行矩阵的乘法操作) -
第一个全连接层的输出形状:
[batch_size,28],这里的28是个人设定的,你也可以设置为别的 -
激活函数不会修改数据的形状
-
第二个全连接层的输出形状:
[batch_size,10],因为手写数字有10个类别
构建模型代码如下:(可以发现:pytorch在构建模型的时候形状上并不会考虑batch_size )
import torch
from torch import nn
import torch.nn.functional as F
class MnistNet(nn.Module):
def __init__(self):
super(MnistNet,self).__init__()
self.fc1 = nn.Linear(28*28*1,28) #定义Linear的输入和输出的形状
self.fc2 = nn.Linear(28,10) #定义Linear的输入和输出的形状
def forward(self,x):
x = x.view(-1,28*28*1) #对数据形状变形,-1表示该位置根据后面的形状自动调整
x = self.fc1(x) #[batch_size,28]
x = F.relu(x) #[batch_size,28]
x = self.fc2(x) #[batch_size,10]手写数字识别是一个多分类问题,一般采用交叉熵损失,在pytorch中,有以下两种方式定义交叉熵损失:
criterion = nn.CrossEntropyLoss()
loss = criterion(input,target)#1. 对输出值计算softmax和取对数
output = F.log_softmax(x,dim=-1)
#2. 使用torch中带权损失
loss = F.nll_loss(output,target)带权损失定义为:![]() ,其实就是把
,其实就是把![]() 作为
作为![]() ,把真实值Y作为权重。
,把真实值Y作为权重。
4.模型的训练
训练的流程:
-
实例化模型,设置模型为训练模式
-
实例化优化器类,实例化损失函数
-
获取,遍历dataloader
-
梯度置为0
-
进行向前计算
-
计算损失
-
反向传播
-
更新参数
mnist_net = MnistNet()
optimizer = optim.Adam(mnist_net.parameters(),lr= 0.001)
def train(epoch):
mode = True
mnist_net.train(mode=mode) #模型设置为训练模型
train_dataloader = get_dataloader(train=mode) #获取训练数据集
for idx,(data,target) in enumerate(train_dataloader):
optimizer.zero_grad() #梯度置为0
output = mnist_net(data) #进行向前计算
loss = F.nll_loss(output,target) #带权损失
loss.backward() #进行反向传播,计算梯度
optimizer.step() #参数更新
if idx % 10 == 0:
print('Train Epoch: {} [{}/{} ({:.0f}%)]\tLoss: {:.6f}'.format(
epoch, idx * len(data), len(train_dataloader.dataset),
100. * idx / len(train_dataloader), loss.item()))5.模型的保存与加载
# 保存
torch.save(mnist_net.state_dict(),"model/mnist_net.pt") #保存模型参数
torch.save(optimizer.state_dict(), 'results/mnist_optimizer.pt') #保存优化器参数
# 加载
mnist_net.load_state_dict(torch.load("model/mnist_net.pt"))
optimizer.load_state_dict(torch.load("results/mnist_optimizer.pt"))6.模型的评估
评估的过程和训练的过程相似,但是:
-
不需要计算梯度
-
需要收集损失和准确率,用来计算平均损失和平均准确率
-
损失的计算和训练时候损失的计算方法相同
-
准确率的计算:
-
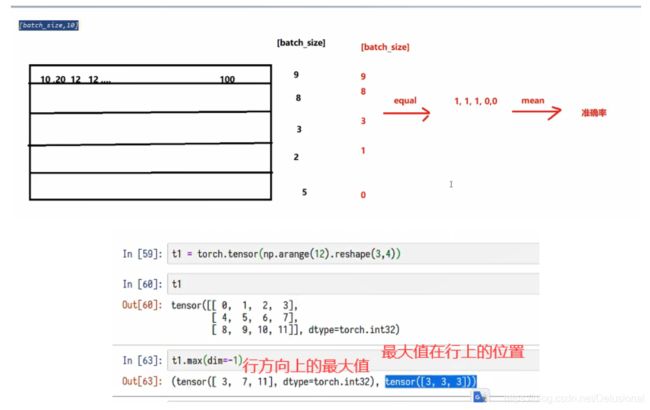
模型的输出为[batch_size,10]的形状
-
其中最大值的位置就是其预测的目标值(预测值进行过sotfmax后为概率,sotfmax中分母都是相同的,分子越大,概率越大)
-
最大值的位置获取的方法可以使用
torch.max,返回最大值和最大值的位置 -
返回最大值的位置后,和真实值(
[batch_size])进行对比,相同表示预测成功
-
def test():
test_loss = 0
correct = 0
mnist_net.eval() #设置模型为评估模式
test_dataloader = get_dataloader(train=False) #获取评估数据集
with torch.no_grad(): #不计算其梯度
for data, target in test_dataloader:
output = mnist_net(data)
test_loss += F.nll_loss(output, target, reduction='sum').item()
pred = output.data.max(1, keepdim=True)[1] #获取最大值的位置,[batch_size,1]
correct += pred.eq(target.data.view_as(pred)).sum() #预测准备样本数累加
test_loss /= len(test_dataloader.dataset) #计算平均损失
print('\nTest set: Avg. loss: {:.4f}, Accuracy: {}/{} ({:.2f}%)\n'.format(
test_loss, correct, len(test_dataloader.dataset),
100. * correct / len(test_dataloader.dataset)))
7.完整代码
import torch
from torch import nn
from torch import optim
import torch.nn.functional as F
import torchvision
train_batch_size = 64
test_batch_size = 1000
img_size = 28
def get_dataloader(train=True):
assert isinstance(train,bool) # "train 必须是bool类型"
#准备数据集,其中0.1307,0.3081为MNIST数据的均值和标准差,这样操作能够对其进行标准化
#因为MNIST只有一个通道(黑白图片),所以元组中只有一个值
dataset = torchvision.datasets.MNIST('/data', train=train, download=True,
transform=torchvision.transforms.Compose([
torchvision.transforms.ToTensor(),
torchvision.transforms.Normalize((0.1307,), (0.3081,)),]))
#准备数据迭代器
batch_size = train_batch_size if train else test_batch_size
dataloader = torch.utils.data.DataLoader(dataset,batch_size=batch_size,shuffle=True)
# 关于dataloader.dataset的长度:训练时为60000,而测试时为10000
return dataloader
class MnistNet(nn.Module):
def __init__(self):
super(MnistNet,self).__init__()
self.fc1 = nn.Linear(28*28*1,28)
self.fc2 = nn.Linear(28,10)
def forward(self,x):
x = x.view(-1,28*28*1)
x = self.fc1(x) #[batch_size,28]
x = F.relu(x) #[batch_size,28]
x = self.fc2(x) #[batch_size,10]
# return x
# 计算softmax和取对数,为计算损失做准备,dim=-1表示取对数的方向(x.shape:[batch_size, 10],对应上面第二种计算损失的方法
return F.log_softmax(x,dim=-1)
mnist_net = MnistNet()
optimizer = optim.Adam(mnist_net.parameters(),lr= 0.001)
# criterion = nn.NLLLoss()
# criterion = nn.CrossEntropyLoss()
train_loss_list = []
# 暂时不知道有啥用
train_count_list = []
def train(epoch):
mode = True
mnist_net.train(mode=mode)
train_dataloader = get_dataloader(train=mode)
# 数据的总数:60000
print(len(train_dataloader.dataset))
# 每批64,那么一共有60000/64,向上取整一共有938
print(len(train_dataloader))
for idx,(data,target) in enumerate(train_dataloader):
optimizer.zero_grad()
output = mnist_net(data)
loss = F.nll_loss(output,target) #对数似然损失
loss.backward()
optimizer.step()
# epoch:训练的批次
# len(data):由train_batch_size决定,这里是64,因此每次输出都是10*64=640
# len(train_dataloader.dataset):60000
# idx / len(train_dataloader):train_dataloader是938(如上),而idx每整10取一次,因此差不多每输出一次就增加百分之一的进度
if idx % 10 == 0:
print('Train Epoch: {} [{}/{} ({:.0f}%)]\tLoss: {:.6f}'.format(
epoch, idx * len(data), len(train_dataloader.dataset),
100. * idx / len(train_dataloader), loss.item()))
train_loss_list.append(loss.item())
# 10 * 64 + (5 - 1)*938
train_count_list.append(idx*train_batch_size+(epoch-1)*len(train_dataloader))
torch.save(mnist_net.state_dict(),"model/mnist_net.pkl")
torch.save(optimizer.state_dict(), 'results/mnist_optimizer.pkl')
def test():
# 测试集的总数据量是10000,而不是60000,而test_batch_size的数值决定了for循环执行的次数,而不决定取出数据量的大小
test_loss = 0
correct = 0
# 评估模式
mnist_net.eval()
# 10000/1000=10
test_dataloader = get_dataloader(train=False)
with torch.no_grad():
for data, target in test_dataloader:
# data.shape:torch.Size([1000, 1, 28, 28])
# target.shape:torch.Size([1000])
output = mnist_net(data)
# reduction默认值是mean,这里取的是sum,相当于每一次都对一个循环内的数据做累加操作(也就是1000个target的损失),所以所有的循环结束后,一共累加了10000个结果的损失,所以后续需要/=len(test_dataloader.dataset)来计算平均损失。这里取默认值mean也是可以的,只是后续除的时候应该除以的是len(test_dataloader)的大小,也就是10000/1000=10。因为用mean的话已经取了一个批次的平均值了。
test_loss += F.nll_loss(output, target, reduction='sum').item()
# 也可以是:pred = output.max(dim = -1)[-1] 两个-1都跟1的意思相同
pred = output.data.max(1, keepdim=True)[1] #获取最大值的位置,形状是[batch_size,1]
# 将预测的目标值和实际的目标值转换为同个形状,方便进行比较,eq的结果如果相同,那么则是True,否则为False,最后用sum方法统计正确的个数,将其累加到correct中
correct += pred.eq(target.data.view_as(pred)).sum()
test_loss /= len(test_dataloader.dataset)
print('\nTest set: Avg. loss: {:.4f}, Accuracy: {}/{} ({:.2f}%)\n'.format(
test_loss, correct, len(test_dataloader.dataset),
100. * correct / len(test_dataloader.dataset)))
if __name__ == '__main__':
test() # 没有训练过的准确率,与后面的形成对比
for i in range(5): #模型训练5轮
train(i)
test()关于代码的解释:
1.输出与真实结果的对比过程
2.获取最大值的位置的原理
计算准确率的另一种写法:
# 获取位置最大值的位置
loss_list = []
acc_list = []
for idx, (input, target) in enumerate(test_dataloader):
with torch.no_grad():
output = model(input)
cur_loss = F.nll_loss(output, target)
loss_list.append(cur_loss)
pred = output.max(dim=-1)[-1]
cur_acc = pred.eq(target).float().mean()
acc_list.append(cur_acc)
print("平均准确率,平均损失:", np.mean(acc_list), np.mean(loss_list))输入如下:(尽管只是全连接层的堆叠,准确率也能到90以上)
Train Epoch: 0 [0/60000 (0%)] Loss: 2.333939
Train Epoch: 0 [640/60000 (1%)] Loss: 1.641663
Train Epoch: 0 [1280/60000 (2%)] Loss: 1.227143
Train Epoch: 0 [1920/60000 (3%)] Loss: 0.988611
Train Epoch: 0 [2560/60000 (4%)] Loss: 0.758898
Train Epoch: 0 [3200/60000 (5%)] Loss: 0.732246
Train Epoch: 0 [3840/60000 (6%)] Loss: 0.603714
Train Epoch: 0 [4480/60000 (7%)] Loss: 0.362477
Train Epoch: 0 [5120/60000 (9%)] Loss: 0.531351
Train Epoch: 0 [5760/60000 (10%)] Loss: 0.506511
Train Epoch: 0 [6400/60000 (11%)] Loss: 0.587733
Train Epoch: 0 [7040/60000 (12%)] Loss: 0.495645
Train Epoch: 0 [7680/60000 (13%)] Loss: 0.257357
Train Epoch: 0 [8320/60000 (14%)] Loss: 0.309358
Train Epoch: 0 [8960/60000 (15%)] Loss: 0.334369
Train Epoch: 0 [9600/60000 (16%)] Loss: 0.432392
Train Epoch: 0 [10240/60000 (17%)] Loss: 0.351203
Train Epoch: 0 [10880/60000 (18%)] Loss: 0.474445
Train Epoch: 0 [11520/60000 (19%)] Loss: 0.327553
Train Epoch: 0 [12160/60000 (20%)] Loss: 0.345029
Train Epoch: 0 [12800/60000 (21%)] Loss: 0.202368
Train Epoch: 0 [13440/60000 (22%)] Loss: 0.380046
Train Epoch: 0 [14080/60000 (23%)] Loss: 0.380915
Train Epoch: 0 [14720/60000 (25%)] Loss: 0.414499
Train Epoch: 0 [15360/60000 (26%)] Loss: 0.286093
Train Epoch: 0 [16000/60000 (27%)] Loss: 0.344182
Train Epoch: 0 [16640/60000 (28%)] Loss: 0.459285
Train Epoch: 0 [17280/60000 (29%)] Loss: 0.304475
Train Epoch: 0 [17920/60000 (30%)] Loss: 0.240846
Train Epoch: 0 [18560/60000 (31%)] Loss: 0.415179
Train Epoch: 0 [19200/60000 (32%)] Loss: 0.367060
Train Epoch: 0 [19840/60000 (33%)] Loss: 0.286321
Train Epoch: 0 [20480/60000 (34%)] Loss: 0.315270
Train Epoch: 0 [21120/60000 (35%)] Loss: 0.365129
Train Epoch: 0 [21760/60000 (36%)] Loss: 0.156136
Train Epoch: 0 [22400/60000 (37%)] Loss: 0.242361
Train Epoch: 0 [23040/60000 (38%)] Loss: 0.135609
Train Epoch: 0 [23680/60000 (39%)] Loss: 0.208712
Train Epoch: 0 [24320/60000 (41%)] Loss: 0.413259
Train Epoch: 0 [24960/60000 (42%)] Loss: 0.314198
Train Epoch: 0 [25600/60000 (43%)] Loss: 0.387002
Train Epoch: 0 [26240/60000 (44%)] Loss: 0.176638
Train Epoch: 0 [26880/60000 (45%)] Loss: 0.595537
Train Epoch: 0 [27520/60000 (46%)] Loss: 0.344560
Train Epoch: 0 [28160/60000 (47%)] Loss: 0.268251
Train Epoch: 0 [28800/60000 (48%)] Loss: 0.132518
Train Epoch: 0 [29440/60000 (49%)] Loss: 0.276750
Train Epoch: 0 [30080/60000 (50%)] Loss: 0.352341
Train Epoch: 0 [30720/60000 (51%)] Loss: 0.222547
Train Epoch: 0 [31360/60000 (52%)] Loss: 0.245519
Train Epoch: 0 [32000/60000 (53%)] Loss: 0.293838
Train Epoch: 0 [32640/60000 (54%)] Loss: 0.383480
Train Epoch: 0 [33280/60000 (55%)] Loss: 0.302779
Train Epoch: 0 [33920/60000 (57%)] Loss: 0.356555
Train Epoch: 0 [34560/60000 (58%)] Loss: 0.457065
Train Epoch: 0 [35200/60000 (59%)] Loss: 0.192767
Train Epoch: 0 [35840/60000 (60%)] Loss: 0.223653
Train Epoch: 0 [36480/60000 (61%)] Loss: 0.323482
Train Epoch: 0 [37120/60000 (62%)] Loss: 0.336282
Train Epoch: 0 [37760/60000 (63%)] Loss: 0.207513
Train Epoch: 0 [38400/60000 (64%)] Loss: 0.163208
Train Epoch: 0 [39040/60000 (65%)] Loss: 0.232840
Train Epoch: 0 [39680/60000 (66%)] Loss: 0.080207
Train Epoch: 0 [40320/60000 (67%)] Loss: 0.347722
Train Epoch: 0 [40960/60000 (68%)] Loss: 0.272386
Train Epoch: 0 [41600/60000 (69%)] Loss: 0.172159
Train Epoch: 0 [42240/60000 (70%)] Loss: 0.227482
Train Epoch: 0 [42880/60000 (71%)] Loss: 0.392149
Train Epoch: 0 [43520/60000 (72%)] Loss: 0.180547
Train Epoch: 0 [44160/60000 (74%)] Loss: 0.325091
Train Epoch: 0 [44800/60000 (75%)] Loss: 0.447692
Train Epoch: 0 [45440/60000 (76%)] Loss: 0.285055
Train Epoch: 0 [46080/60000 (77%)] Loss: 0.151321
Train Epoch: 0 [46720/60000 (78%)] Loss: 0.300437
Train Epoch: 0 [47360/60000 (79%)] Loss: 0.360237
Train Epoch: 0 [48000/60000 (80%)] Loss: 0.229651
Train Epoch: 0 [48640/60000 (81%)] Loss: 0.173506
Train Epoch: 0 [49280/60000 (82%)] Loss: 0.373799
Train Epoch: 0 [49920/60000 (83%)] Loss: 0.310182
Train Epoch: 0 [50560/60000 (84%)] Loss: 0.325685
Train Epoch: 0 [51200/60000 (85%)] Loss: 0.377012
Train Epoch: 0 [51840/60000 (86%)] Loss: 0.209962
Train Epoch: 0 [52480/60000 (87%)] Loss: 0.256001
Train Epoch: 0 [53120/60000 (88%)] Loss: 0.143939
Train Epoch: 0 [53760/60000 (90%)] Loss: 0.270528
Train Epoch: 0 [54400/60000 (91%)] Loss: 0.272074
Train Epoch: 0 [55040/60000 (92%)] Loss: 0.271088
Train Epoch: 0 [55680/60000 (93%)] Loss: 0.246737
Train Epoch: 0 [56320/60000 (94%)] Loss: 0.181094
Train Epoch: 0 [56960/60000 (95%)] Loss: 0.402492
Train Epoch: 0 [57600/60000 (96%)] Loss: 0.196838
Train Epoch: 0 [58240/60000 (97%)] Loss: 0.328228
Train Epoch: 0 [58880/60000 (98%)] Loss: 0.228163
Train Epoch: 0 [59520/60000 (99%)] Loss: 0.325608
Test set: Avg. loss: 0.2356, Accuracy: 9275/10000 (92.75%)