《动手学深度学习PyTorch版》打卡_Task8，文本分类，数据增强，模型微调

        最近参加了伯禹平台和Datawhale等举办的《动手学深度学习PyTorch版》课程，对文本分类，数据增强，模型微调做下笔记。

---

文本情感分类

文本分类是自然语言处理的一个常见任务，它把一段不定长的文本序列变换为文本的类别。本节关注它的一个子问题：使用文本情感分类来分析文本作者的情绪。这个问题也叫情感分析，并有着广泛的应用。

同搜索近义词和类比词一样，文本分类也属于词嵌入的下游应用。在本节中，我们将应用预训练的词向量和含多个隐藏层的双向循环神经网络与卷积神经网络，来判断一段不定长的文本序列中包含的是正面还是负面的情绪。后续内容将从以下几个方面展开：

1. 文本情感分类数据集
2. 使用循环神经网络进行情感分类
3. 使用卷积神经网络进行情感分类

文本情感分类数据

我们使用斯坦福的IMDb数据集（Stanford’s Large Movie Review Dataset）作为文本情感分类的数据集。

读取数据，编码，替换'\n',打上标签

预处理数据

读取数据后，我们先根据文本的格式进行单词的切分，再利用 torchtext.vocab.Vocab 创建词典。

词典和词语的索引创建好后，就可以将数据集的文本从字符串的形式转换为单词下标序列的形式，以待之后的使用

并截断或者padding补0，固定长度为500

实现双向循环神经网络，下面是以 LSTM 为例的代码

class BiRNN(nn.Module):
    def __init__(self, vocab, embed_size, num_hiddens, num_layers):
        '''
        @params:
            vocab: 在数据集上创建的词典，用于获取词典大小
            embed_size: 嵌入维度大小
            num_hiddens: 隐藏状态维度大小
            num_layers: 隐藏层个数
        '''
        super(BiRNN, self).__init__()
        self.embedding = nn.Embedding(len(vocab), embed_size)
        
        # encoder-decoder framework
        # bidirectional设为True即得到双向循环神经网络
        self.encoder = nn.LSTM(input_size=embed_size, 
                                hidden_size=num_hiddens, 
                                num_layers=num_layers,
                                bidirectional=True)
        self.decoder = nn.Linear(4*num_hiddens, 2) # 初始时间步和最终时间步的隐藏状态作为全连接层输入
        
    def forward(self, inputs):
        '''
        @params:
            inputs: 词语下标序列，形状为 (batch_size, seq_len) 的整数张量
        @return:
            outs: 对文本情感的预测，形状为 (batch_size, 2) 的张量
        '''
        # 因为LSTM需要将序列长度(seq_len)作为第一维，所以需要将输入转置
        embeddings = self.embedding(inputs.permute(1, 0)) # (seq_len, batch_size, d)
        # rnn.LSTM 返回输出、隐藏状态和记忆单元，格式如 outputs, (h, c)
        outputs, _ = self.encoder(embeddings) # (seq_len, batch_size, 2*h)
        encoding = torch.cat((outputs[0], outputs[-1]), -1) # (batch_size, 4*h)
        outs = self.decoder(encoding) # (batch_size, 2)
        return outs

embed_size, num_hiddens, num_layers = 100, 100, 2
net = BiRNN(vocab, embed_size, num_hiddens, num_layers)

加载预训练的词向量

由于预训练词向量的词典及词语索引与我们使用的数据集并不相同，所以需要根据目前的词典及索引的顺序来加载预训练词向量。

注意不需要更新它embedding的参数

cache_dir = "/home/kesci/input/GloVe6B5429"
glove_vocab = Vocab.GloVe(name='6B', dim=100, cache=cache_dir)

def load_pretrained_embedding(words, pretrained_vocab):
    '''
    @params:
        words: 需要加载词向量的词语列表，以 itos (index to string) 的词典形式给出
        pretrained_vocab: 预训练词向量
    @return:
        embed: 加载到的词向量
    '''
    embed = torch.zeros(len(words), pretrained_vocab.vectors[0].shape[0]) # 初始化为0
    oov_count = 0 # out of vocabulary
    for i, word in enumerate(words):
        try:
            idx = pretrained_vocab.stoi[word]
            embed[i, :] = pretrained_vocab.vectors[idx]
        except KeyError:
            oov_count += 1
    if oov_count > 0:
        print("There are %d oov words." % oov_count)
    return embed

net.embedding.weight.data.copy_(load_pretrained_embedding(vocab.itos, glove_vocab))
net.embedding.weight.requires_grad = False # 直接加载预训练好的, 所以不需要更新它

由于嵌入层的参数是不需要在训练过程中被更新的，所以我们利用 filter 函数和 lambda 表达式来过滤掉模型中不需要更新参数的部分。

lr, num_epochs = 0.01, 5
optimizer = torch.optim.Adam(filter(lambda p: p.requires_grad, net.parameters()), lr=lr)
loss = nn.CrossEntropyLoss()

train(train_iter, test_iter, net, loss, optimizer, device, num_epochs)

使用卷积神经网络

一维卷积层

在介绍模型前我们先来解释一维卷积层的工作原理。与二维卷积层一样，一维卷积层使用一维的互相关运算。如图所示，输入是一个宽为 7 的一维数组，核数组的宽为 2。可以看到输出的宽度为 7−2+1=6，且第一个元素是由输入的最左边的宽为 2 的子数组与核数组按元素相乘后再相加得到的：0×1+1×2=2。

多输入通道的一维互相关运算也与多输入通道的二维互相关运算类似：在每个通道上，将核与相应的输入做一维互相关运算，并将通道之间的结果相加得到输出结果。下图展示了含 3 个输入通道的一维互相关运算，其中阴影部分为第一个输出元素及其计算所使用的输入和核数组元素：0×1+1×2+1×3+2×4+2×(−1)+3×(−3)=2。

由二维互相关运算的定义可知，多输入通道的一维互相关运算可以看作单输入通道的二维互相关运算。如图所示，我们也可以将图中多输入通道的一维互相关运算以等价的单输入通道的二维互相关运算呈现。这里核的高等于输入的高。图中的阴影部分为第一个输出元素及其计算所使用的输入和核数组元素：2×(−1)+3×(−3)+1×3+2×4+0×1+1×2=2。

注：反之仅当二维卷积核的高度等于输入的高度时才成立。

之前的例子中输出都只有一个通道。类似地，我们也可以在一维卷积层指定多个输出通道，从而拓展卷积层中的模型参数。

时序最大池化层

类似地，我们有一维池化层。TextCNN 中使用的时序最大池化（max-over-time pooling）层实际上对应一维全局最大池化层：假设输入包含多个通道，各通道由不同时间步上的数值组成，各通道的输出即该通道所有时间步中最大的数值。因此，时序最大池化层的输入在各个通道上的时间步数可以不同。

注：自然语言中还有一些其他的池化操作，可参考这篇https://blog.csdn.net/malefactor/article/details/51078135

TextCNN 模型

TextCNN 模型主要使用了一维卷积层和时序最大池化层。假设输入的文本序列由 n 个词组成，每个词用 d 维的词向量表示。那么输入样本的宽为 n，输入通道数为 d。TextCNN 的计算主要分为以下几步。

1. 定义多个一维卷积核，并使用这些卷积核对输入分别做卷积计算。宽度不同的卷积核可能会捕捉到不同个数的相邻词的相关性。
2. 对输出的所有通道分别做时序最大池化，再将这些通道的池化输出值连结为向量。
3. 通过全连接层将连结后的向量变换为有关各类别的输出。这一步可以使用丢弃层应对过拟合。

下图用一个例子解释了 TextCNN 的设计。这里的输入是一个有 11 个词的句子，每个词用 6 维词向量表示。因此输入序列的宽为 11，输入通道数为 6。给定 2 个一维卷积核，核宽分别为 2 和 4，输出通道数分别设为 4 和 5。因此，一维卷积计算后，4 个输出通道的宽为 11−2+1=10，而其他 5 个通道的宽为 11−4+1=8。尽管每个通道的宽不同，我们依然可以对各个通道做时序最大池化，并将 9 个通道的池化输出连结成一个 9 维向量。最终，使用全连接将 9 维向量变换为 2 维输出，即正面情感和负面情感的预测。

---

数据增强

图像增广

图像增广（image augmentation）技术通过对训练图像做一系列随机改变，来产生相似但又不同的训练样本，从而扩大训练数据集的规模。图像增广的另一种解释是，随机改变训练样本可以降低模型对某些属性的依赖，从而提高模型的泛化能力。例如，我们可以对图像进行不同方式的裁剪，使感兴趣的物体出现在不同位置，从而减轻模型对物体出现位置的依赖性。我们也可以调整亮度、色彩等因素来降低模型对色彩的敏感度。可以说，在当年AlexNet的成功中，图像增广技术功不可没。本节我们将讨论这个在计算机视觉里被广泛使用的技术。

常用的图像增广方法

我们来读取一张形状为400×500（高和宽分别为400像素和500像素）的图像作为实验的样例。

翻转和裁剪

左右翻转图像通常不改变物体的类别。它是最早也是最广泛使用的一种图像增广方法。

在我们使用的样例图像里，猫在图像正中间，但一般情况下可能不是这样。在5.4节（池化层）里我们解释了池化层能降低卷积层对目标位置的敏感度。除此之外，我们还可以通过对图像随机裁剪来让物体以不同的比例出现在图像的不同位置，这同样能够降低模型对目标位置的敏感性。

上下翻转不如左右翻转通用。但是至少对于样例图像，上下翻转不会造成识别障碍。

随机裁剪出一块面积为原面积10%∼100%的区域，且该区域的宽和高之比随机取自0.5∼2，然后再将该区域的宽和高分别缩放到200像素。若无特殊说明，本节中a和b之间的随机数指的是从区间[a,b]中随机均匀采样所得到的连续值。

 

变化颜色

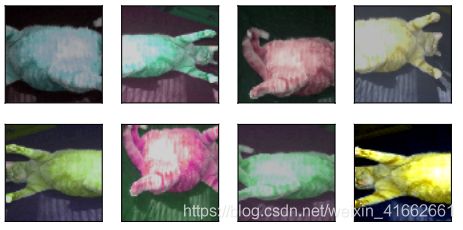
另一类增广方法是变化颜色。我们可以从4个方面改变图像的颜色：亮度（brightness）、对比度（contrast）、饱和度（saturation）和色调（hue）。在下面的例子里，我们将图像的亮度随机变化为原图亮度的50%(1−0.5)∼150%(1+0.5)。

 叠加多个图像增广方法

实际应用中我们会将多个图像增广方法叠加使用。我们可以通过Compose实例将上面定义的多个图像增广方法叠加起来，再应用到每张图像之上。

为了在预测时得到确定的结果，我们通常只将图像增广应用在训练样本上，而不在预测时使用含随机操作的图像增广。

---

 模型微调

 

迁移学习中的一种常用技术：微调（fine tuning）。如图所示，微调由以下4步构成。

1. 在源数据集（如ImageNet数据集）上预训练一个神经网络模型，即源模型。
2. 创建一个新的神经网络模型，即目标模型。它复制了源模型上除了输出层外的所有模型设计及其参数。我们假设这些模型参数包含了源数据集上学习到的知识，且这些知识同样适用于目标数据集。我们还假设源模型的输出层跟源数据集的标签紧密相关，因此在目标模型中不予采用。
3. 为目标模型添加一个输出大小为目标数据集类别个数的输出层，并随机初始化该层的模型参数。
4. 在目标数据集（如椅子数据集）上训练目标模型。我们将从头训练输出层，而其余层的参数都是基于源模型的参数微调得到的。

当目标数据集远小于源数据集时，微调有助于提升模型的泛化能力。